Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Morishita, Masanori
1991.
On S-class number relations of algebraic tori in Galois extensions of global fields.
Nagoya Mathematical Journal,
Vol. 124,
Issue. ,
p.
133.
González-Avilés, Cristian D.
2010.
On Néron-Raynaud class groups of tori and the capitulation problem.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2010,
Issue. 648,
González-Avilés, Cristian D.
2020.
Cokernels of restriction maps and subgroups of norm one, with applications to quadratic Galois coverings.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 2,
p.
559.
Hung, Fan-Yun
and
Yu, Chia-Fu
2024.
Class numbers of multinorm-one tori.
Journal of Number Theory,
Vol. 258,
Issue. ,
p.
94.


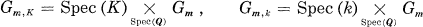 .
.