Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-24T18:11:36.745Z Has data issue: false hasContentIssue false
  • English
  • Français

SIMPLE GROUPS, PRODUCT ACTIONS, AND GENERALIZED QUADRANGLES

Part of: Designs and configurations Finite geometry and special incidence structures Permutation groups

Published online by Cambridge University Press:  14 September 2017

JOHN BAMBERG ,
TOMASZ POPIEL  and
CHERYL E. PRAEGER
JOHN BAMBERG
Affiliation:
Centre for the Mathematics of Symmetry and Computation, School of Mathematics and Statistics, The University of Western Australia, 35 Stirling Highway, Crawley, W.A. 6009, Australia email john.bamberg@uwa.edu.au
TOMASZ POPIEL
Affiliation:
Centre for the Mathematics of Symmetry and Computation, School of Mathematics and Statistics, The University of Western Australia, 35 Stirling Highway, Crawley, W.A. 6009, Australia School of Mathematical Sciences, Queen Mary University of London, Mile End Road, London E1 4NS, UK email tomasz.popiel@uwa.edu.au
CHERYL E. PRAEGER
Affiliation:
Centre for the Mathematics of Symmetry and Computation, School of Mathematics and Statistics, The University of Western Australia, 35 Stirling Highway, Crawley, W.A. 6009, Australia King Abdulaziz University, Jeddah 21589, Saudi Arabia email cheryl.praeger@uwa.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

The classification of flag-transitive generalized quadrangles is a long-standing open problem at the interface of finite geometry and permutation group theory. Given that all known flag-transitive generalized quadrangles are also point-primitive (up to point–line duality), it is likewise natural to seek a classification of the point-primitive examples. Working toward this aim, we are led to investigate generalized quadrangles that admit a collineation group 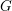$G$ preserving a Cartesian product decomposition of the set of points. It is shown that, under a generic assumption on 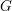$G$, the number of factors of such a Cartesian product can be at most four. This result is then used to treat various types of primitive and quasiprimitive point actions. In particular, it is shown that 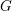$G$ cannot have holomorph compound O’Nan–Scott type. Our arguments also pose purely group-theoretic questions about conjugacy classes in nonabelian finite simple groups and fixities of primitive permutation groups.

MSC classification

Primary: 51E12: Generalized quadrangles, generalized polygons
Secondary: 20B15: Primitive groups 05B25: Finite geometries
Type
Article
Information
Nagoya Mathematical Journal , Volume 234 , June 2019 , pp. 87 - 126
Copyright
© 2017 Foundation Nagoya Mathematical Journal  

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

John Bamberg is supported by the Australian Research Council Future Fellowship FT120100036. Tomasz Popiel and Cheryl E. Praeger are supported by the Australian Research Council Discovery Grant DP140100416.

References

Babai, L., On the automorphism groups of strongly regular graphs II , J. Algebra 421 (2015), 560–578.10.1016/j.jalgebra.2014.09.007Google Scholar
Baddeley, R. W., Primitive permutation groups with a regular non-abelian normal subgroup , Proc. Lond. Math. Soc. 67 (1993), 547–595.Google Scholar
Bamberg, J., Betten, A., Cara, P., De Beule, J., Lavrauw, M. and Neunhöffer, M., FinInG–Finite Incidence Geometry, Version 1.0, 2014.Google Scholar
Bamberg, J. and Giudici, M., Point regular groups of automorphisms of generalised quadrangles , J. Combin. Theory Ser. A 118 (2011), 1114–1128.10.1016/j.jcta.2010.11.004Google Scholar
Bamberg, J., Giudici, M., Morris, J., Royle, G. F. and Spiga, P. , Generalised quadrangles with a group of automorphisms acting primitively on points and lines , J. Combin. Theory Ser. A 119 (2012), 1479–1499.10.1016/j.jcta.2012.04.005Google Scholar
Bamberg, J., Glasby, S. P., Popiel, T. and Praeger, C. E., Generalised quadrangles and transitive pseudo-hyperovals , J. Combin. Des. 24 (2016), 151–164.10.1002/jcd.21411Google Scholar
Bamberg, J., Glasby, S. P., Popiel, T., Praeger, C. E. and Schneider, C., Point-primitive generalised hexagons and octagons , J. Combin. Theory Ser. A 147 (2017), 186–204.Google Scholar
Bamberg, J., Popiel, T. and Praeger, C. E., Point-primitive, line-transitive generalised quadrangles of holomorph type , J. Group Theory 20 (2017), 269–287.Google Scholar
Burness, T. C. and Giudici, M., Classical Groups, Derangements, and Primes, Australian Mathematical Society Lecture Series 25 , Cambridge University Press, Cambridge, 2016.Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., ATLAS of Finite Groups, Oxford University Press, Oxford, 1985.Google Scholar
Covato, E., The involution fixity of simple groups, Ph.D. thesis, University of Bristol, 2017.Google Scholar
De Winter, S. and Thas, K., Generalized quadrangles with an abelian Singer group , Des. Codes Cryptogr. 39 (2006), 81–87.10.1007/s10623-005-2747-zGoogle Scholar
Feit, W. and Thompson, J. G., Solvability of groups of odd order , Pacific J. Math. 13 (1963), 775–1029.10.2140/pjm.1963.13.775Google Scholar
Frohardt, D. and Magaard, K., Fixed point ratios in exceptional groups of rank at most two , Comm. Algebra 30 (2002), 571–602.Google Scholar
The GAP Group, GAP–Groups, Algorithms, and Programming, Version 4.7.8, 2015.Google Scholar
Ghinelli, D., Regular groups on generalized quadrangles and nonabelian difference sets with multiplier - 1 , Geom. Dedicata 41 (1992), 165–174.Google Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The Classification of the Finite Simple Groups, Number 3, Mathematical Surveys and Monographs 40 , American Mathematical Society, Providence, 1998.Google Scholar
Liebeck, M. W. and Seitz, G. M., Unipotent and Nilpotent Classes in Simple Algebraic Groups and Lie Algebras, Mathematical Surveys and Monographs 180 , American Mathematical Society, Providence, RI, 2012.10.1090/surv/180Google Scholar
Liebeck, M. W. and Shalev, A., On fixed points of elements in primitive permutation groups , J. Algebra 421 (2015), 438–459.10.1016/j.jalgebra.2014.08.038Google Scholar
Morgan, L. and Popiel, T., Generalised polygons admitting a point-primitive almost simple group of Suzuki or Ree type , Electron. J. Combin. 23 (2016), P1.34.Google Scholar
Payne, S. E. and Thas, J. A., Finite Generalized Quadrangles, Pitman, London, 1984.Google Scholar
Praeger, C. E., Li, C.-H. and Niemeyer, A. C., “ Finite transitive permutation groups and finite vertex-transitive graphs ”, in Graph Symmetry, (eds. Hahn, G. and Sabidussi, G.) Kluwer, 1997, 277–318.10.1007/978-94-015-8937-6_7Google Scholar
Spaltenstein, N., Caractères unipotents de 3D4(F q ) , Comment. Math. Helv. 57 (1982), 676–691.Google Scholar
Suzuki, M., On a class of doubly transitive groups , Annals Math. 75 (1962), 105–145.Google Scholar
Tits, J., Sur la trialité et certains groupes qui s’en déduisent , Publ. Math. Inst. Hautes Études Sci. 2 (1959), 13–60.Google Scholar
Van Maldeghem, H., Generalized Polygons, Birkháuser, Basel, 1998.Google Scholar
Yoshiara, S., A generalized quadrangle with an automorphism group acting regularly on the points , European J. Combin. 28 (2007), 653–664.Google Scholar