Article contents
ON THE GALOIS STRUCTURE OF ARITHMETIC COHOMOLOGY I: COMPACTLY SUPPORTED 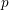 $p$-ADIC COHOMOLOGY
$p$-ADIC COHOMOLOGY
Published online by Cambridge University Press: 16 November 2018
Abstract
We investigate the Galois structures of 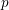 $p$-adic cohomology groups of general
$p$-adic cohomology groups of general 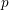 $p$-adic representations over finite extensions of number fields. We show, in particular, that as the field extensions vary over natural families the Galois modules formed by these cohomology groups always decompose as the direct sum of a projective module and a complementary module of bounded
$p$-adic representations over finite extensions of number fields. We show, in particular, that as the field extensions vary over natural families the Galois modules formed by these cohomology groups always decompose as the direct sum of a projective module and a complementary module of bounded 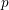 $p$-rank. We use this result to derive new (upper and lower) bounds on the changes in ranks of Selmer groups over extensions of number fields and descriptions of the explicit Galois structures of natural arithmetic modules.
$p$-rank. We use this result to derive new (upper and lower) bounds on the changes in ranks of Selmer groups over extensions of number fields and descriptions of the explicit Galois structures of natural arithmetic modules.
MSC classification
- Type
- Article
- Information
- Copyright
- © 2018 Foundation Nagoya Mathematical Journal
References
- 1
- Cited by



