Hostname: page-component-7bb8b95d7b-lvwk9 Total loading time: 0 Render date: 2024-09-24T13:25:15.782Z Has data issue: false hasContentIssue false
  • English
  • Français

On Segre products of affine semigroup rings

Published online by Cambridge University Press:  22 January 2016

Lê Tuân Hoa
Lê Tuân Hoa*
Affiliation:
Institute of Mathematics, P. O. Box 631, Bò Hô, Hanoi, Vietnam
*
Sektion Mathematik, M. L. Universität Halle, Halle (S) 4010, DDR
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let N denote the set of non-negative integers. An affine semigroup is a finitely generated submonoid S of the additive monoid Nm for some positive integer m. Let k[S] denote the semigroup ring of S over a field k. Then one can identify k[S] with the subring of a polynomial ring k[t1, …, tm] generated by the monomials .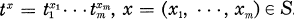

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 110 , June 1988 , pp. 113 - 128
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1988

References

[1] Badescu, L., On certain isolated singularities, Nagoya Math. J., 61 (1976), 205–220.Google Scholar
[2] Barcanescu, S., Gorensteiness of Segre-Veronese graded algebras, preprint 1979.Google Scholar
[3] Barshay, J., On the zeta function of biprojective complete intersections, Trans. Amer. Math. Soc, 135 (1969), 447–458.Google Scholar
[4] Chow, W. L., On unmixedness theorem, Amer. J. Math., 86 (1964), 799–822.Google Scholar
[5] Cooke, G. E. and Finney, R. L., Homology of cell complexes, Math. Notes, Princeton Univ. Press 1967.Google Scholar
[6] Cuong, N. T., Schenzel, P. and Trung, N. V., Verallgemeinerte Cohen-Maeaulay-Moduln, Math. Nachr., 85 (1978), 57–73.Google Scholar
[7] Goto, S., Buchsbaum rings of maximal embedding dimension, J. Algebra, 76 (1982), 494–508.CrossRefGoogle Scholar
[8] Goto, S. and Watanabe, K., On graded rings I, J. Math. Soc. Japan, 30 (1978), 179–213.Google Scholar
[9] Hartshorne, R., Algebraic geometry, Springer-Verlag, 1977.Google Scholar
[10] Reisner, G., Cohen-Macaulay quotients of polynomial rings, Adv. in Math., 21 (1976), 30–49.CrossRefGoogle Scholar
[11] Solean, S., Über die Abhángigkeit der Buchsbaum-Eigenschaft von der Charakteristik des Grundkörpers, Math. Slovaka, 31 (1981), 437–444.Google Scholar
[12] Spanier, E. H., Algebraic topology, McGraw-Hill, 1966.Google Scholar
[13] Stanley, R. P., Linear diophantine equations and local cohomology, Invent. Math., 68 (1982), 175–193.Google Scholar
[14] Stückrad, J. and Vogel, W., Toward a theory of Buchsbaum singularities, Amer. J. Math., 100 (1978), 726–746.Google Scholar
[15] Trung, N. V., Classification of the double projections of Veronese varieties, J. Math. Kyoto Univ., 22 (1983), 567–581.Google Scholar
[16] Trung, N. V. and Hoa, L. T., Affine semigroups and Cohen-Macaulay rings generated by monomials, Trans. Amer. Math. Soc, 298 (1986), 145–167.CrossRefGoogle Scholar
[17] Trung, N. V. and Ikeda, S., When is the Rees algebra Cohen-Macaulay, preprint.Google Scholar