Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-22T11:14:35.987Z Has data issue: false hasContentIssue false
  • English
  • Français

On compact minimal hypersurfaces in a sphere with constant scalar curvature

Published online by Cambridge University Press:  22 January 2016

Naoya Doi
Naoya Doi*
Affiliation:
Department of Mathematics, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be an n-dimensional hypersurface immersed in the (n + 1)-dimensional unit sphere Sn+1 with the standard metric by an immersion f. We denote by A the second fundamental form of the immersion / which is considered as a symmetric linear transformation of each tangent space TXM, i.e. for an arbitrary point x of M and the unit normal vector field ξ defined in a neighborhood of x, A is given by 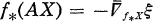where 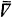is the covariant differentiation in Sn+i and 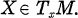Thus, A depends on the orientation of the unit normal vector field ξ and, in general, it is locally defined on M.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 78 , May 1980 , pp. 177 - 188
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1980

References

[1] Cheng, S. Y. and Yau, S. T., Hypersurfaces with constant scalar curvature, Math. Ann. 225 (1977), 195–204.Google Scholar
[2] Chern, S. S., Carmo, M. do and Kobayashi, S., Minimal submanifolds of a sphere with second fundamental form of constant length. Functional Analysis and Related Fields (1970), 59–75.Google Scholar
[3] Hsiang, W. Y., Remarks on closed minimal submanifolds in the standard ra-sphere, J. Diff. Geom. 1 (1967), 257–267.Google Scholar
[4] Lawson, H. B., Local rigidity theorems for minimal hypersurfaces, Ann. of Math. 89 (1969), 187–197.CrossRefGoogle Scholar
[5] Nomizu, K. and Smyth, B., A formula of Simons’ type and Hypersurfaces with constant mean curvature, J. Diff. Geom. 3 (1969), 367–377.Google Scholar
[6] Pinl, M. and Ziller, W., Minimal hypersurfaces in a space of constant curvature, J. Diff. Geom. 11 (1976), 335–343.Google Scholar
[7] Ryan, P. J., Homogeneity and some curvature conditions for hypersurfaces, Tohoku Math. Journ. 21 (1969), 363–388.Google Scholar
[8] Simons, J., Minimal varieties in riemannian manifolds, Ann. of Math. 88 (1968), 62–105.Google Scholar
[9] Sternberg, S., Lectures on differential geometry, Prentice-Hall (1964).Google Scholar
[10] Yau, S. T., Submanifolds with constant mean curvature II, Amer. J. of Math. 97 (1973), 76–100.Google Scholar