1 Introduction
The objective of this paper is to find suitable conditions on the local cohomology modules of multi-Rees algebras and associated graded rings of multigraded admissible filtrations of ideals in an analytically unramified local ring
![]() $(R,\mathfrak{m})$
and apply these to detect their joint reduction vectors and completeness of products of complete ideals.
$(R,\mathfrak{m})$
and apply these to detect their joint reduction vectors and completeness of products of complete ideals.
Recall that if
![]() $R$
is a commutative ring and
$R$
is a commutative ring and
![]() $I$
is an ideal of
$I$
is an ideal of
![]() $R$
, then
$R$
, then
![]() $a\in R$
is called integral over
$a\in R$
is called integral over
![]() $I$
, if
$I$
, if
![]() $a$
is a root of a monic polynomial
$a$
is a root of a monic polynomial
![]() $x^{n}+a_{1}x^{n-1}+\cdots +a_{n-1}x+a_{n}$
for some
$x^{n}+a_{1}x^{n-1}+\cdots +a_{n-1}x+a_{n}$
for some
![]() $a_{i}\in I^{i}$
for
$a_{i}\in I^{i}$
for
![]() $i=1,2,\ldots ,n$
. The integral closure of
$i=1,2,\ldots ,n$
. The integral closure of
![]() $I$
, denoted by
$I$
, denoted by
![]() $\overline{I}$
, is the set of all elements of
$\overline{I}$
, is the set of all elements of
![]() $R$
that are integral over
$R$
that are integral over
![]() $I$
. If
$I$
. If
![]() $I=\overline{I}$
, then
$I=\overline{I}$
, then
![]() $I$
is called complete or integrally closed. Zariski [Reference Zariski15] proved that the product of complete ideals is complete in the polynomial ring
$I$
is called complete or integrally closed. Zariski [Reference Zariski15] proved that the product of complete ideals is complete in the polynomial ring
![]() $k[x,y]$
, where
$k[x,y]$
, where
![]() $k$
is an algebraically closed field of characteristic zero. This was generalized to two-dimensional regular local rings in [Reference Zariski and Samuel16, Appendix 5]. This result is known as Zariski’s product theorem. Huneke [Reference Huneke5] showed that the product of complete ideals is not complete in higher-dimensional regular local rings. Since the appearance of this counterexample of Huneke, several results have appeared in the literature which identify classes of complete ideals in local rings of dimension at least 3 whose products are complete. The following result due to Reid, Roberts and Vitulli [Reference Reid, Roberts and Vitulli13, Proposition 3.1] about complete monomial ideals is rather surprising.
$k$
is an algebraically closed field of characteristic zero. This was generalized to two-dimensional regular local rings in [Reference Zariski and Samuel16, Appendix 5]. This result is known as Zariski’s product theorem. Huneke [Reference Huneke5] showed that the product of complete ideals is not complete in higher-dimensional regular local rings. Since the appearance of this counterexample of Huneke, several results have appeared in the literature which identify classes of complete ideals in local rings of dimension at least 3 whose products are complete. The following result due to Reid, Roberts and Vitulli [Reference Reid, Roberts and Vitulli13, Proposition 3.1] about complete monomial ideals is rather surprising.
Theorem 1.1. Let
![]() $R=k[X_{1},\ldots ,X_{d}]$
be a polynomial ring of dimension
$R=k[X_{1},\ldots ,X_{d}]$
be a polynomial ring of dimension
![]() $d\geqslant 1$
over a field
$d\geqslant 1$
over a field
![]() $k$
. Let
$k$
. Let
![]() $I$
be a monomial ideal of
$I$
be a monomial ideal of
![]() $R$
so that
$R$
so that
![]() $I^{n}$
is complete for all
$I^{n}$
is complete for all
![]() $1\leqslant n\leqslant d-1$
. Then,
$1\leqslant n\leqslant d-1$
. Then,
![]() $I^{n}$
is complete for all
$I^{n}$
is complete for all
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
This can be thought of as a partial generalization of Zariski’s product theorem for
![]() $d=2$
. This theorem was proved using tools from convex geometry. In this paper, we approach this result using vanishing of local cohomology modules of multi-Rees algebras, and prove the following result about completeness of power products of
$d=2$
. This theorem was proved using tools from convex geometry. In this paper, we approach this result using vanishing of local cohomology modules of multi-Rees algebras, and prove the following result about completeness of power products of
![]() $\mathfrak{m}$
-primary monomial ideals.
$\mathfrak{m}$
-primary monomial ideals.
Theorem 1.2. Let
![]() $R=k[X_{1},\ldots ,X_{d}]$
be a polynomial ring over a field
$R=k[X_{1},\ldots ,X_{d}]$
be a polynomial ring over a field
![]() $k$
, let
$k$
, let
![]() $d\geqslant 1$
, and let
$d\geqslant 1$
, and let
![]() $\mathfrak{m}$
be the maximal homogeneous ideal of
$\mathfrak{m}$
be the maximal homogeneous ideal of
![]() $R$
. Let
$R$
. Let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary monomial ideals of
$\mathfrak{m}$
-primary monomial ideals of
![]() $R$
. Suppose that
$R$
. Suppose that
![]() $\mathbf{I}^{\mathbf{n}}$
is complete for all
$\mathbf{I}^{\mathbf{n}}$
is complete for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
such that
$\mathbf{n}\in \mathbb{N}^{s}$
such that
![]() $1\leqslant |\mathbf{n}|\leqslant d-1$
. Then,
$1\leqslant |\mathbf{n}|\leqslant d-1$
. Then,
![]() $\mathbf{I}^{\mathbf{n}}$
is complete for all
$\mathbf{I}^{\mathbf{n}}$
is complete for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
with
$\mathbf{n}\in \mathbb{N}^{s}$
with
![]() $|\mathbf{n}|\geqslant 1$
.
$|\mathbf{n}|\geqslant 1$
.
We prove the above result as a consequence of a more general result for complete ideals in analytically unramified local rings. In order to state this and other results proved in this paper, we recall certain definitions and set up notation.
Throughout this paper,
![]() $(R,\mathfrak{m})$
denotes a Noetherian local ring of dimension
$(R,\mathfrak{m})$
denotes a Noetherian local ring of dimension
![]() $d$
with infinite residue field. Let
$d$
with infinite residue field. Let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals of
$\mathfrak{m}$
-primary ideals of
![]() $R$
, and we denote the collection of these ideals
$R$
, and we denote the collection of these ideals
![]() $(I_{1},\ldots ,I_{s})$
by
$(I_{1},\ldots ,I_{s})$
by
![]() $\mathbf{I}$
. For
$\mathbf{I}$
. For
![]() $s\geqslant 1$
, we put
$s\geqslant 1$
, we put
![]() $\mathbf{e}=(1,\ldots ,1),\;\mathbf{0}=(0,\ldots ,0)\in \mathbb{Z}^{s}$
, and for all
$\mathbf{e}=(1,\ldots ,1),\;\mathbf{0}=(0,\ldots ,0)\in \mathbb{Z}^{s}$
, and for all
![]() $i=1,\ldots ,s$
,
$i=1,\ldots ,s$
,
![]() $\mathbf{e}_{\mathbf{i}}=(0,\ldots ,1,\ldots ,0)\in \mathbb{Z}^{s}$
, where
$\mathbf{e}_{\mathbf{i}}=(0,\ldots ,1,\ldots ,0)\in \mathbb{Z}^{s}$
, where
![]() $1$
occurs at
$1$
occurs at
![]() $i$
th position. For
$i$
th position. For
![]() $\mathbf{n}=(n_{1},\ldots ,n_{s})\in \mathbb{Z}^{s}$
, we write
$\mathbf{n}=(n_{1},\ldots ,n_{s})\in \mathbb{Z}^{s}$
, we write
![]() $\mathbf{I}^{\mathbf{n}}=I_{1}^{n_{1}}\cdots I_{s}^{n_{s}}$
and
$\mathbf{I}^{\mathbf{n}}=I_{1}^{n_{1}}\cdots I_{s}^{n_{s}}$
and
![]() $\mathbf{n}^{+}=(n_{1}^{+},\ldots ,n_{s}^{+})$
, where
$\mathbf{n}^{+}=(n_{1}^{+},\ldots ,n_{s}^{+})$
, where
![]() $n_{i}^{+}=\max \{0,n_{i}\}$
. For
$n_{i}^{+}=\max \{0,n_{i}\}$
. For
![]() $s\geqslant 2$
and
$s\geqslant 2$
and
![]() $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{s})\in \mathbb{N}^{s}$
, we put
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{s})\in \mathbb{N}^{s}$
, we put
![]() $|\unicode[STIX]{x1D6FC}|=\unicode[STIX]{x1D6FC}_{1}+\cdots +\unicode[STIX]{x1D6FC}_{s}$
. We define
$|\unicode[STIX]{x1D6FC}|=\unicode[STIX]{x1D6FC}_{1}+\cdots +\unicode[STIX]{x1D6FC}_{s}$
. We define
![]() $\mathbf{m}=(m_{1},\ldots ,m_{s})\geqslant \mathbf{n}=(n_{1},\ldots ,n_{s})$
if
$\mathbf{m}=(m_{1},\ldots ,m_{s})\geqslant \mathbf{n}=(n_{1},\ldots ,n_{s})$
if
![]() $m_{i}\geqslant n_{i}$
for all
$m_{i}\geqslant n_{i}$
for all
![]() $i=1,\ldots ,s$
. By the phrase “for all large
$i=1,\ldots ,s$
. By the phrase “for all large
![]() $\mathbf{n}$
”, we mean
$\mathbf{n}$
”, we mean
![]() $\mathbf{n}\in \mathbb{N}^{s}$
and
$\mathbf{n}\in \mathbb{N}^{s}$
and
![]() $n_{i}\gg 0$
for all
$n_{i}\gg 0$
for all
![]() $i=1,\ldots ,s$
.
$i=1,\ldots ,s$
.
Definition 1.3. A set of ideals
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
is called a
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
is called a
![]() $\mathbb{Z}^{s}$
-graded
$\mathbb{Z}^{s}$
-graded
![]() $\mathbf{I}$
-filtration if for all
$\mathbf{I}$
-filtration if for all
![]() $\mathbf{m},\mathbf{n}\in \mathbb{Z}^{s}$
, (i)
$\mathbf{m},\mathbf{n}\in \mathbb{Z}^{s}$
, (i)
![]() $\mathbf{I}^{\mathbf{n}}\subseteq {\mathcal{F}}(\mathbf{n})$
, (ii)
$\mathbf{I}^{\mathbf{n}}\subseteq {\mathcal{F}}(\mathbf{n})$
, (ii)
![]() ${\mathcal{F}}(\mathbf{n}){\mathcal{F}}(\mathbf{m})\subseteq {\mathcal{F}}(\mathbf{n}+\mathbf{m})$
and (iii) if
${\mathcal{F}}(\mathbf{n}){\mathcal{F}}(\mathbf{m})\subseteq {\mathcal{F}}(\mathbf{n}+\mathbf{m})$
and (iii) if
![]() $\mathbf{m}\geqslant \mathbf{n}$
,
$\mathbf{m}\geqslant \mathbf{n}$
,
![]() ${\mathcal{F}}(\mathbf{m})\subseteq {\mathcal{F}}(\mathbf{n})$
.
${\mathcal{F}}(\mathbf{m})\subseteq {\mathcal{F}}(\mathbf{n})$
.
Let
![]() $t_{1},\ldots ,t_{s}$
be indeterminates. For
$t_{1},\ldots ,t_{s}$
be indeterminates. For
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
, we put
$\mathbf{n}\in \mathbb{Z}^{s}$
, we put
![]() $\mathbf{t}^{\mathbf{n}}=t_{1}^{n_{1}}\cdots t_{s}^{n_{s}}$
and denote the
$\mathbf{t}^{\mathbf{n}}=t_{1}^{n_{1}}\cdots t_{s}^{n_{s}}$
and denote the
![]() $\mathbb{N}^{s}$
-graded Rees ring of
$\mathbb{N}^{s}$
-graded Rees ring of
![]() ${\mathcal{F}}$
by
${\mathcal{F}}$
by
![]() ${\mathcal{R}}({\mathcal{F}})=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}{\mathcal{F}}(\mathbf{n})\mathbf{t}^{\mathbf{n}}$
and the
${\mathcal{R}}({\mathcal{F}})=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}{\mathcal{F}}(\mathbf{n})\mathbf{t}^{\mathbf{n}}$
and the
![]() $\mathbb{Z}^{s}$
-graded extended Rees ring of
$\mathbb{Z}^{s}$
-graded extended Rees ring of
![]() ${\mathcal{F}}$
by
${\mathcal{F}}$
by
![]() ${\mathcal{R}}^{\prime }({\mathcal{F}})=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}{\mathcal{F}}(\mathbf{n})\mathbf{t}^{\mathbf{n}}$
. For an
${\mathcal{R}}^{\prime }({\mathcal{F}})=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}{\mathcal{F}}(\mathbf{n})\mathbf{t}^{\mathbf{n}}$
. For an
![]() $\mathbb{N}^{s}$
-graded ring
$\mathbb{N}^{s}$
-graded ring
![]() $S=\bigoplus _{\mathbf{n}\geqslant \mathbf{0}}S_{\mathbf{n}}$
, we denote the ideal
$S=\bigoplus _{\mathbf{n}\geqslant \mathbf{0}}S_{\mathbf{n}}$
, we denote the ideal
![]() $\bigoplus _{\mathbf{n}\geqslant \mathbf{e}}S_{\mathbf{n}}$
by
$\bigoplus _{\mathbf{n}\geqslant \mathbf{e}}S_{\mathbf{n}}$
by
![]() $S_{++}$
. Let
$S_{++}$
. Let
![]() $G({\mathcal{F}})=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}{\mathcal{F}}(\mathbf{n})/{\mathcal{F}}(\mathbf{n}+\mathbf{e})$
be the associated multigraded ring of
$G({\mathcal{F}})=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}{\mathcal{F}}(\mathbf{n})/{\mathcal{F}}(\mathbf{n}+\mathbf{e})$
be the associated multigraded ring of
![]() ${\mathcal{F}}$
with respect to
${\mathcal{F}}$
with respect to
![]() ${\mathcal{F}}(\mathbf{e})$
. For
${\mathcal{F}}(\mathbf{e})$
. For
![]() ${\mathcal{F}}=\{\mathbf{I}^{\mathbf{n}}\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
, we set
${\mathcal{F}}=\{\mathbf{I}^{\mathbf{n}}\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
, we set
![]() ${\mathcal{R}}({\mathcal{F}})={\mathcal{R}}(\mathbf{I})$
,
${\mathcal{R}}({\mathcal{F}})={\mathcal{R}}(\mathbf{I})$
,
![]() ${\mathcal{R}}^{\prime }({\mathcal{F}})={\mathcal{R}}^{\prime }(\mathbf{I})$
,
${\mathcal{R}}^{\prime }({\mathcal{F}})={\mathcal{R}}^{\prime }(\mathbf{I})$
,
![]() $G({\mathcal{F}})=G(\mathbf{I})$
and
$G({\mathcal{F}})=G(\mathbf{I})$
and
![]() ${\mathcal{R}}(\mathbf{I})_{++}={\mathcal{R}}_{++}$
.
${\mathcal{R}}(\mathbf{I})_{++}={\mathcal{R}}_{++}$
.
Definition 1.4. A
![]() $\mathbb{Z}^{s}$
-graded
$\mathbb{Z}^{s}$
-graded
![]() $\mathbf{I}$
-filtration
$\mathbf{I}$
-filtration
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
of ideals in
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
of ideals in
![]() $R$
is called an
$R$
is called an
![]() $\mathbf{I}$
-admissible filtration if
$\mathbf{I}$
-admissible filtration if
![]() ${\mathcal{F}}(\mathbf{n})={\mathcal{F}}(\mathbf{n}^{+})$
for all
${\mathcal{F}}(\mathbf{n})={\mathcal{F}}(\mathbf{n}^{+})$
for all
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
and
$\mathbf{n}\in \mathbb{Z}^{s}$
and
![]() ${\mathcal{R}}^{\prime }({\mathcal{F}})$
is a finite
${\mathcal{R}}^{\prime }({\mathcal{F}})$
is a finite
![]() ${\mathcal{R}}^{\prime }(\mathbf{I})$
-module.
${\mathcal{R}}^{\prime }(\mathbf{I})$
-module.
The principal examples of admissible filtrations with which we are concerned in this paper are (i) the
![]() $\mathbf{I}$
-adic filtration
$\mathbf{I}$
-adic filtration
![]() $\{\mathbf{I}^{\mathbf{n}}\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
in a Noetherian local ring and (ii) the integral closure filtration
$\{\mathbf{I}^{\mathbf{n}}\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
in a Noetherian local ring and (ii) the integral closure filtration
![]() $\{\overline{\mathbf{I}^{\mathbf{n}}}\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
in an analytically unramified local ring. It is proved in [Reference Masuti, Sarkar and Verma11, Proposition 2.5] that if
$\{\overline{\mathbf{I}^{\mathbf{n}}}\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
in an analytically unramified local ring. It is proved in [Reference Masuti, Sarkar and Verma11, Proposition 2.5] that if
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
is an
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
is an
![]() $\mathbf{I}$
-admissible filtration of ideals in
$\mathbf{I}$
-admissible filtration of ideals in
![]() $R$
, then
$R$
, then
![]() ${\mathcal{R}}({\mathcal{F}})$
is a finitely generated
${\mathcal{R}}({\mathcal{F}})$
is a finitely generated
![]() ${\mathcal{R}}(\mathbf{I})$
-module.
${\mathcal{R}}(\mathbf{I})$
-module.
Recall that an ideal
![]() $J$
contained in an ideal
$J$
contained in an ideal
![]() $I$
is called a reduction of
$I$
is called a reduction of
![]() $I$
if
$I$
if
![]() $JI^{n}=I^{n+1}$
for all large
$JI^{n}=I^{n+1}$
for all large
![]() $n$
. The role that reductions of ideals play in the study of Hilbert–Samuel functions of
$n$
. The role that reductions of ideals play in the study of Hilbert–Samuel functions of
![]() $\mathfrak{m}$
-primary ideals is played by joint reductions, introduced by Rees in [Reference Rees12], of a sequence of
$\mathfrak{m}$
-primary ideals is played by joint reductions, introduced by Rees in [Reference Rees12], of a sequence of
![]() $\mathfrak{m}$
-primary ideals
$\mathfrak{m}$
-primary ideals
![]() $I_{1},\ldots ,I_{s}$
to study the multigraded Hilbert–Samuel function
$I_{1},\ldots ,I_{s}$
to study the multigraded Hilbert–Samuel function
![]() $H(\mathbf{I},\mathbf{n})=\unicode[STIX]{x1D706}(R/\mathbf{I}^{\mathbf{n}})$
. Let
$H(\mathbf{I},\mathbf{n})=\unicode[STIX]{x1D706}(R/\mathbf{I}^{\mathbf{n}})$
. Let
![]() $\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
, and let
$\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
, and let
![]() $|\mathbf{q}|=d\geqslant 1$
. A set of elements
$|\mathbf{q}|=d\geqslant 1$
. A set of elements
![]() $\{a_{ij}\in I_{i}\mid i=1,\ldots ,s;j=1,\ldots ,q_{i}\}$
is called a joint reduction of the set of ideals
$\{a_{ij}\in I_{i}\mid i=1,\ldots ,s;j=1,\ldots ,q_{i}\}$
is called a joint reduction of the set of ideals
![]() $(I_{1},\ldots ,I_{s})$
of type
$(I_{1},\ldots ,I_{s})$
of type
![]() $\mathbf{q}$
if there exists an
$\mathbf{q}$
if there exists an
![]() $\mathbf{m}\in \mathbb{N}^{s}$
so that, for all
$\mathbf{m}\in \mathbb{N}^{s}$
so that, for all
![]() $\mathbf{n}\geqslant \mathbf{m}$
,
$\mathbf{n}\geqslant \mathbf{m}$
,
The vector
![]() $\mathbf{m}$
is called a joint reduction vector. We estimate joint reduction vectors using local cohomology modules of multi-Rees rings. In order to achieve this, we need to work with joint reductions in a more general setting. Kirby and Rees [Reference Kirby and Rees9] generalized it further in the setting of multigraded rings and modules, which we recall next.
$\mathbf{m}$
is called a joint reduction vector. We estimate joint reduction vectors using local cohomology modules of multi-Rees rings. In order to achieve this, we need to work with joint reductions in a more general setting. Kirby and Rees [Reference Kirby and Rees9] generalized it further in the setting of multigraded rings and modules, which we recall next.
Definition 1.5. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
![]() $\mathbb{N}^{s}$
-graded ring defined over a local ring
$\mathbb{N}^{s}$
-graded ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
, and let
$(R_{\mathbf{0}},\mathfrak{m})$
, and let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finite
$M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finite
![]() $\mathbb{Z}^{s}$
-graded
$\mathbb{Z}^{s}$
-graded
![]() $R$
-module. A joint reduction of type
$R$
-module. A joint reduction of type
![]() $\mathbf{q}$
of
$\mathbf{q}$
of
![]() $R$
with respect to
$R$
with respect to
![]() $M$
is a set of elements
$M$
is a set of elements
generating an ideal
![]() $J$
of
$J$
of
![]() $R$
irrelevant with respect to
$R$
irrelevant with respect to
![]() $M$
; that is,
$M$
; that is,
![]() $(JM)_{\mathbf{n}}=M_{\mathbf{n}}$
for all large
$(JM)_{\mathbf{n}}=M_{\mathbf{n}}$
for all large
![]() $\mathbf{n}$
.
$\mathbf{n}$
.
Kirby and Rees [Reference Kirby and Rees9] proved the existence of joint reduction of type
![]() $\mathbf{q}$
of
$\mathbf{q}$
of
![]() $R$
with respect to
$R$
with respect to
![]() $M$
if
$M$
if
![]() $|\mathbf{q}|\geqslant \text{dim}\left(\frac{M}{\mathfrak{m}M}\right)+1$
and if the residue field
$|\mathbf{q}|\geqslant \text{dim}\left(\frac{M}{\mathfrak{m}M}\right)+1$
and if the residue field
![]() $R_{\mathbf{0}}/\mathfrak{m}$
is infinite. Here,
$R_{\mathbf{0}}/\mathfrak{m}$
is infinite. Here,
![]() $\text{dim}\,R$
is defined to be
$\text{dim}\,R$
is defined to be
![]() $\max (\text{ht}\,P)$
, where
$\max (\text{ht}\,P)$
, where
![]() $P$
ranges over the relevant prime ideals of
$P$
ranges over the relevant prime ideals of
![]() $R$
if
$R$
if
![]() $R$
is not trivial and
$R$
is not trivial and
![]() $-1$
if
$-1$
if
![]() $R$
is trivial. For
$R$
is trivial. For
![]() $M$
,
$M$
,
![]() $\text{dim}\,M$
is defined to be
$\text{dim}\,M$
is defined to be
![]() $\text{dim}\left(\frac{R}{\text{Ann}_{R}\,M}\right)$
.
$\text{dim}\left(\frac{R}{\text{Ann}_{R}\,M}\right)$
.
Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of dimension
$(R,\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d\geqslant 1$
, let
$d\geqslant 1$
, let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals of
$\mathfrak{m}$
-primary ideals of
![]() $R$
, and let
$R$
, and let
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be a
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be a
![]() $\mathbb{Z}^{s}$
-graded
$\mathbb{Z}^{s}$
-graded
![]() $\mathbf{I}$
-admissible filtration of ideals in
$\mathbf{I}$
-admissible filtration of ideals in
![]() $R$
. Let
$R$
. Let
![]() $\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
, such that
$\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
, such that
![]() $|\mathbf{q}|=d$
.
$|\mathbf{q}|=d$
.
Definition 1.6. A set of elements
![]() ${\mathcal{A}}_{\mathbf{q}}({\mathcal{F}})=\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
is called a joint reduction of
${\mathcal{A}}_{\mathbf{q}}({\mathcal{F}})=\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
is called a joint reduction of
![]() ${\mathcal{F}}$
of type
${\mathcal{F}}$
of type
![]() $\mathbf{q}$
if the set
$\mathbf{q}$
if the set
![]() $\{a_{ij}t_{i}\in {\mathcal{R}}(\mathbf{I})_{\mathbf{e_{i}}}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
is a joint reduction of type
$\{a_{ij}t_{i}\in {\mathcal{R}}(\mathbf{I})_{\mathbf{e_{i}}}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
is a joint reduction of type
![]() $\mathbf{q}$
of
$\mathbf{q}$
of
![]() ${\mathcal{R}}(\mathbf{I})$
with respect to
${\mathcal{R}}(\mathbf{I})$
with respect to
![]() ${\mathcal{R}}({\mathcal{F}})$
; that is, the following equality holds for all
${\mathcal{R}}({\mathcal{F}})$
; that is, the following equality holds for all
![]() $\mathbf{n}\geqslant \mathbf{m}$
for some
$\mathbf{n}\geqslant \mathbf{m}$
for some
![]() $\mathbf{m}\in \mathbb{N}^{s}$
:
$\mathbf{m}\in \mathbb{N}^{s}$
:
The vector
![]() $\mathbf{m}$
is called a joint reduction vector of
$\mathbf{m}$
is called a joint reduction vector of
![]() ${\mathcal{F}}$
with respect to the joint reduction
${\mathcal{F}}$
with respect to the joint reduction
![]() ${\mathcal{A}}_{\mathbf{q}}({\mathcal{F}})$
.
${\mathcal{A}}_{\mathbf{q}}({\mathcal{F}})$
.
Let
![]() $I,J$
be
$I,J$
be
![]() $\mathfrak{m}$
-primary ideals in a Noetherian local ring
$\mathfrak{m}$
-primary ideals in a Noetherian local ring
![]() $(R,\mathfrak{m})$
of dimension
$(R,\mathfrak{m})$
of dimension
![]() $d\geqslant 2$
,
$d\geqslant 2$
,
![]() $\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\geqslant 1$
and
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}\geqslant 1$
and
![]() $\unicode[STIX]{x1D707}+\unicode[STIX]{x1D706}=d$
. For the bigraded filtration
$\unicode[STIX]{x1D707}+\unicode[STIX]{x1D706}=d$
. For the bigraded filtration
![]() ${\mathcal{F}}=\{I^{r}J^{s}\}_{r,s\in \mathbb{Z}}$
and a joint reduction
${\mathcal{F}}=\{I^{r}J^{s}\}_{r,s\in \mathbb{Z}}$
and a joint reduction
Hyry [Reference Hyry7] defined the joint reduction number of
![]() ${\mathcal{F}}$
with respect to
${\mathcal{F}}$
with respect to
![]() ${\mathcal{A}}(\unicode[STIX]{x1D707},\unicode[STIX]{x1D706})$
to be the smallest integer
${\mathcal{A}}(\unicode[STIX]{x1D707},\unicode[STIX]{x1D706})$
to be the smallest integer
![]() $n$
satisfying
$n$
satisfying
We adapt this definition to define the joint reduction number for multigraded filtrations.
Definition 1.7. Let
![]() $\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
, such that
$\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
, such that
![]() $|\mathbf{q}|=d\geqslant 1$
. The joint reduction number of
$|\mathbf{q}|=d\geqslant 1$
. The joint reduction number of
![]() ${\mathcal{F}}$
with respect to a joint reduction
${\mathcal{F}}$
with respect to a joint reduction
is the smallest integer
![]() $n\in \mathbb{N}$
, denoted by
$n\in \mathbb{N}$
, denoted by
![]() $\text{jr}_{{\mathcal{A}}_{\mathbf{q}}}({\mathcal{F}})$
, such that for all
$\text{jr}_{{\mathcal{A}}_{\mathbf{q}}}({\mathcal{F}})$
, such that for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
and
$\mathbf{n}\in \mathbb{N}^{s}$
and
![]() $A=\{i|q_{i}\neq 0\}$
,
$A=\{i|q_{i}\neq 0\}$
,
We define the joint reduction number of
![]() ${\mathcal{F}}$
of type
${\mathcal{F}}$
of type
![]() $\mathbf{q}$
to be
$\mathbf{q}$
to be
A crucial step in our investigations is to establish a connection between joint reduction vectors and vanishing of multigraded components of local cohomology modules of multi-Rees algebras. The following result of Hyry plays a crucial role.
Lemma 1.8. [Reference Hyry7, Lemma 2.3]
Let
![]() $S$
be a Noetherian
$S$
be a Noetherian
![]() $\mathbb{Z}$
-graded ring defined over a local ring
$\mathbb{Z}$
-graded ring defined over a local ring
![]() $(R,\mathfrak{m})$
. Let
$(R,\mathfrak{m})$
. Let
![]() ${\mathcal{M}}$
be the homogeneous maximal ideal of
${\mathcal{M}}$
be the homogeneous maximal ideal of
![]() $S$
. Let
$S$
. Let
![]() $\mathfrak{a}\subset \mathfrak{m}$
be an ideal. Let
$\mathfrak{a}\subset \mathfrak{m}$
be an ideal. Let
![]() $M$
be a finitely generated
$M$
be a finitely generated
![]() $\mathbb{Z}$
-graded
$\mathbb{Z}$
-graded
![]() $S$
-module, and let
$S$
-module, and let
![]() $n_{0}\in \mathbb{Z}$
. Then,
$n_{0}\in \mathbb{Z}$
. Then,
![]() $[H_{{\mathcal{M}}}^{i}(M)]_{n}=0$
for all
$[H_{{\mathcal{M}}}^{i}(M)]_{n}=0$
for all
![]() $n\geqslant n_{0}$
and
$n\geqslant n_{0}$
and
![]() $i\geqslant 0$
if and only if
$i\geqslant 0$
if and only if
![]() $[H_{(\mathfrak{a},S_{+})}^{i}(M)]_{n}=0$
for all
$[H_{(\mathfrak{a},S_{+})}^{i}(M)]_{n}=0$
for all
![]() $n\geqslant n_{0}$
and
$n\geqslant n_{0}$
and
![]() $i\geqslant 0$
.
$i\geqslant 0$
.
For convenience, inspired by the above result, we introduce an invariant of local cohomology modules of multigraded modules over multigraded rings. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
![]() $\mathbb{N}^{s}$
-graded ring defined over a local ring
$\mathbb{N}^{s}$
-graded ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
. Let
$(R_{\mathbf{0}},\mathfrak{m})$
. Let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{Z}^{s}$
-graded
$\mathbb{Z}^{s}$
-graded
![]() $R$
-module.
$R$
-module.
Definition 1.9. Let
![]() $\mathbf{m}\in \mathbb{Z}^{s}$
. We say that the module
$\mathbf{m}\in \mathbb{Z}^{s}$
. We say that the module
![]() $M$
satisfies Hyry’s condition
$M$
satisfies Hyry’s condition
![]() $\text{H}_{R}(M,\mathbf{m})$
if
$\text{H}_{R}(M,\mathbf{m})$
if
Suppose that
![]() $R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
$R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
![]() $i=1,\ldots ,s$
. Let
$i=1,\ldots ,s$
. Let
![]() ${\mathcal{M}}$
be the maximal homogeneous ideal of
${\mathcal{M}}$
be the maximal homogeneous ideal of
![]() $R$
, for each
$R$
, for each
![]() $i=1,\ldots ,s$
, let
$i=1,\ldots ,s$
, let
![]() ${\mathcal{M}}_{i}$
be the ideal of
${\mathcal{M}}_{i}$
be the ideal of
![]() $R$
generated by
$R$
generated by
![]() $R_{\mathbf{e}_{\mathbf{i}}}$
, and let
$R_{\mathbf{e}_{\mathbf{i}}}$
, and let
![]() $R_{++}=\bigcap _{i}{\mathcal{M}}_{i}$
.
$R_{++}=\bigcap _{i}{\mathcal{M}}_{i}$
.
Let
![]() $I$
be any subset of
$I$
be any subset of
![]() $\{1,\ldots ,s\}$
, and let
$\{1,\ldots ,s\}$
, and let
![]() $J$
be a nonempty subset of
$J$
be a nonempty subset of
![]() $\{1,\ldots ,s\}$
. Then, for disjoint
$\{1,\ldots ,s\}$
. Then, for disjoint
![]() $I$
and
$I$
and
![]() $J$
, we define
$J$
, we define
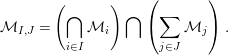 $$\begin{eqnarray}{\mathcal{M}}_{I,J}=\left(\mathop{\bigcap }_{i\in I}{\mathcal{M}}_{i}\right)\bigcap \left(\mathop{\sum }_{j\in J}{\mathcal{M}}_{j}\right).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}_{I,J}=\left(\mathop{\bigcap }_{i\in I}{\mathcal{M}}_{i}\right)\bigcap \left(\mathop{\sum }_{j\in J}{\mathcal{M}}_{j}\right).\end{eqnarray}$$
We prove a multigraded version of the above result due to Hyry.
Proposition 1.10. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
![]() $\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
$\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
,
$(R_{\mathbf{0}},\mathfrak{m})$
,
![]() $R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
$R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
![]() $i=1,\ldots ,s$
, and let
$i=1,\ldots ,s$
, and let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{N}^{s}$
-graded
$\mathbb{N}^{s}$
-graded
![]() $R$
-module. Let
$R$
-module. Let
![]() $I$
be any subset of
$I$
be any subset of
![]() $\{1,\ldots ,s\}$
, and let
$\{1,\ldots ,s\}$
, and let
![]() $J$
be a nonempty subset of
$J$
be a nonempty subset of
![]() $\{1,\ldots ,s\}$
, such that
$\{1,\ldots ,s\}$
, such that
![]() $I$
and
$I$
and
![]() $J$
are disjoint. Suppose that
$J$
are disjoint. Suppose that
![]() $\mathbf{a}=(a_{1},\ldots ,a_{s})\in \mathbb{Z}^{s}$
and
$\mathbf{a}=(a_{1},\ldots ,a_{s})\in \mathbb{Z}^{s}$
and
![]() $[H_{{\mathcal{M}}}^{i}(M)]_{\mathbf{n}}=0$
for all
$[H_{{\mathcal{M}}}^{i}(M)]_{\mathbf{n}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
, such that
$\mathbf{n}\in \mathbb{Z}^{s}$
, such that
![]() $n_{k}>a_{k}$
for at least one
$n_{k}>a_{k}$
for at least one
![]() $k\in \{1,\ldots ,s\}$
. Then,
$k\in \{1,\ldots ,s\}$
. Then,
![]() $[H_{{\mathcal{M}}_{I,J}}^{i}(M)]_{\mathbf{n}}=0$
for all
$[H_{{\mathcal{M}}_{I,J}}^{i}(M)]_{\mathbf{n}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\geqslant \mathbf{a}+\mathbf{e}$
. In particular,
$\mathbf{n}\geqslant \mathbf{a}+\mathbf{e}$
. In particular,
![]() $M$
satisfies Hyry’s condition
$M$
satisfies Hyry’s condition
![]() $\text{H}_{R}(M,\mathbf{a}+\mathbf{e})$
.
$\text{H}_{R}(M,\mathbf{a}+\mathbf{e})$
.
In order to detect joint reduction vectors of multigraded admissible filtrations, we use the theory of filter-regular sequences for multigraded modules.
Definition 1.11. A homogeneous element
![]() $a\in R$
is called an
$a\in R$
is called an
![]() $M$
-filter-regular if
$M$
-filter-regular if
![]() $(0:_{M}a)_{\mathbf{n}}=0$
for all large
$(0:_{M}a)_{\mathbf{n}}=0$
for all large
![]() $\mathbf{n}$
. Let
$\mathbf{n}$
. Let
![]() $a_{1},\ldots ,a_{r}\in R$
be homogeneous elements. Then,
$a_{1},\ldots ,a_{r}\in R$
be homogeneous elements. Then,
![]() $a_{1},\ldots ,a_{r}$
is called an
$a_{1},\ldots ,a_{r}$
is called an
![]() $M$
-filter-regular sequence if
$M$
-filter-regular sequence if
![]() $a_{i}$
is
$a_{i}$
is
![]() $M/(a_{1},\ldots ,a_{i-1})M$
-filter-regular for all
$M/(a_{1},\ldots ,a_{i-1})M$
-filter-regular for all
![]() $i=1,\ldots ,r$
.
$i=1,\ldots ,r$
.
Theorem 1.12. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of dimension
$(R,\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d\geqslant 1$
, and let
$d\geqslant 1$
, and let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals in
$\mathfrak{m}$
-primary ideals in
![]() $R$
. Let
$R$
. Let
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
![]() $\mathbf{I}$
-admissible filtration of ideals in
$\mathbf{I}$
-admissible filtration of ideals in
![]() $R$
. Suppose that
$R$
. Suppose that
![]() $G({\mathcal{F}})$
satisfies Hyry’s condition
$G({\mathcal{F}})$
satisfies Hyry’s condition
![]() $\text{H}_{G(\mathbf{I})}(G({\mathcal{F}}),\mathbf{m})$
. Let
$\text{H}_{G(\mathbf{I})}(G({\mathcal{F}}),\mathbf{m})$
. Let
![]() $\mathbf{q}\in \mathbb{N}^{s}$
such that
$\mathbf{q}\in \mathbb{N}^{s}$
such that
![]() $|\mathbf{q}|=d$
, and let
$|\mathbf{q}|=d$
, and let
![]() $\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
be a joint reduction of
$\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
be a joint reduction of
![]() ${\mathcal{F}}$
of type
${\mathcal{F}}$
of type
![]() $\mathbf{q}$
such that
$\mathbf{q}$
such that
![]() $a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast }$
is a
$a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast }$
is a
![]() $G({\mathcal{F}})$
-filter-regular sequence, where
$G({\mathcal{F}})$
-filter-regular sequence, where
![]() $a_{ij}^{\ast }$
is the image of
$a_{ij}^{\ast }$
is the image of
![]() $a_{ij}$
in
$a_{ij}$
in
![]() $G(\mathbf{I})_{\mathbf{e}_{\mathbf{i}}}$
for all
$G(\mathbf{I})_{\mathbf{e}_{\mathbf{i}}}$
for all
![]() $j=1,\ldots ,q_{i}$
and
$j=1,\ldots ,q_{i}$
and
![]() $i=1,\ldots ,s$
. Then,
$i=1,\ldots ,s$
. Then,
We can now state the main theorem of this paper, which gives a generalization of the Reid–Roberts–Vitulli theorem for zero-dimensional monomial ideals.
Theorem 1.13. Let
![]() $(R,\mathfrak{m})$
be an analytically unramified Noetherian local ring of dimension
$(R,\mathfrak{m})$
be an analytically unramified Noetherian local ring of dimension
![]() $d\geqslant 2$
, and let
$d\geqslant 2$
, and let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals in
$\mathfrak{m}$
-primary ideals in
![]() $R$
. Let
$R$
. Let
![]() $\overline{{\mathcal{R}}}(\mathbf{I})=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}\overline{\mathbf{I}^{\mathbf{n}}}$
satisfy the condition
$\overline{{\mathcal{R}}}(\mathbf{I})=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}\overline{\mathbf{I}^{\mathbf{n}}}$
satisfy the condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}(\overline{{\mathcal{R}}}(\mathbf{I}),\mathbf{0})$
. Suppose that
$\text{H}_{{\mathcal{R}}(\mathbf{I})}(\overline{{\mathcal{R}}}(\mathbf{I}),\mathbf{0})$
. Suppose that
![]() $\mathbf{I}^{\mathbf{n}}$
is complete for all
$\mathbf{I}^{\mathbf{n}}$
is complete for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
such that
$\mathbf{n}\in \mathbb{N}^{s}$
such that
![]() $1\leqslant |\mathbf{n}|\leqslant d-1$
. Then,
$1\leqslant |\mathbf{n}|\leqslant d-1$
. Then,
![]() $\mathbf{I}^{\mathbf{n}}$
is complete for all
$\mathbf{I}^{\mathbf{n}}$
is complete for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
with
$\mathbf{n}\in \mathbb{N}^{s}$
with
![]() $|\mathbf{n}|\geqslant 1$
.
$|\mathbf{n}|\geqslant 1$
.
We prove that if
![]() $\overline{{\mathcal{R}}}(\mathbf{I})$
is Cohen–Macaulay, then it satisfies Hyry’s condition
$\overline{{\mathcal{R}}}(\mathbf{I})$
is Cohen–Macaulay, then it satisfies Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}(\overline{{\mathcal{R}}}(\mathbf{I}),\mathbf{0})$
. By Hochster’s theorem [Reference Bruns and Herzog2, Theorem 6.3.5] about Cohen–Macaulayness of normal semigroup rings,
$\text{H}_{{\mathcal{R}}(\mathbf{I})}(\overline{{\mathcal{R}}}(\mathbf{I}),\mathbf{0})$
. By Hochster’s theorem [Reference Bruns and Herzog2, Theorem 6.3.5] about Cohen–Macaulayness of normal semigroup rings,
![]() $\overline{{\mathcal{R}}}(\mathbf{I})$
is Cohen–Macaulay if
$\overline{{\mathcal{R}}}(\mathbf{I})$
is Cohen–Macaulay if
![]() $\mathbf{I}$
consists of monomial ideals in a polynomial ring over a field.
$\mathbf{I}$
consists of monomial ideals in a polynomial ring over a field.
2 Existence of joint reductions consisting of filter-regular sequences
Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
![]() $\mathbb{N}^{s}$
-graded ring defined over an Artinian local ring
$\mathbb{N}^{s}$
-graded ring defined over an Artinian local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
. Let
$(R_{\mathbf{0}},\mathfrak{m})$
. Let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{N}^{s}$
-graded
$\mathbb{N}^{s}$
-graded
![]() $R$
-module. Let
$R$
-module. Let
![]() $\text{Proj}^{s}(R)$
denote the set of all homogeneous prime ideals
$\text{Proj}^{s}(R)$
denote the set of all homogeneous prime ideals
![]() $P$
in
$P$
in
![]() $R$
such that
$R$
such that
![]() $R_{++}\nsubseteq P$
and
$R_{++}\nsubseteq P$
and
![]() $M^{\unicode[STIX]{x1D6E5}}=\bigoplus _{n\geqslant 0}M_{n\mathbf{e}}$
. Let
$M^{\unicode[STIX]{x1D6E5}}=\bigoplus _{n\geqslant 0}M_{n\mathbf{e}}$
. Let
![]() $\text{dim}\,M^{\unicode[STIX]{x1D6E5}}=d$
. By [Reference Herrmann, Hyry, Ribbe and Tang3, Theorem 4.1], there exists a numerical polynomial
$\text{dim}\,M^{\unicode[STIX]{x1D6E5}}=d$
. By [Reference Herrmann, Hyry, Ribbe and Tang3, Theorem 4.1], there exists a numerical polynomial
![]() $P_{M}\in \mathbb{Q}[X_{1},\ldots ,X_{s}]$
of total degree
$P_{M}\in \mathbb{Q}[X_{1},\ldots ,X_{s}]$
of total degree
![]() $d-1$
of the form
$d-1$
of the form
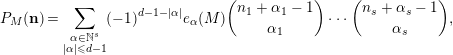 $$\begin{eqnarray}P_{M}(\mathbf{n})=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}\in \mathbb{N}^{s} \\ |\unicode[STIX]{x1D6FC}|\leqslant d-1}}(-1)^{d-1-|\unicode[STIX]{x1D6FC}|}e_{\unicode[STIX]{x1D6FC}}(M)\binom{n_{1}+\unicode[STIX]{x1D6FC}_{1}-1}{\unicode[STIX]{x1D6FC}_{1}}\cdots \binom{n_{s}+\unicode[STIX]{x1D6FC}_{s}-1}{\unicode[STIX]{x1D6FC}_{s}},\end{eqnarray}$$
$$\begin{eqnarray}P_{M}(\mathbf{n})=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}\in \mathbb{N}^{s} \\ |\unicode[STIX]{x1D6FC}|\leqslant d-1}}(-1)^{d-1-|\unicode[STIX]{x1D6FC}|}e_{\unicode[STIX]{x1D6FC}}(M)\binom{n_{1}+\unicode[STIX]{x1D6FC}_{1}-1}{\unicode[STIX]{x1D6FC}_{1}}\cdots \binom{n_{s}+\unicode[STIX]{x1D6FC}_{s}-1}{\unicode[STIX]{x1D6FC}_{s}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{s})$
, such that
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{s})$
, such that
![]() $e_{\unicode[STIX]{x1D6FC}}(M)\in \mathbb{Z}$
,
$e_{\unicode[STIX]{x1D6FC}}(M)\in \mathbb{Z}$
,
![]() $P_{M}(\mathbf{n})=\unicode[STIX]{x1D706}_{R_{\mathbf{0}}}(M_{\mathbf{n}})$
for all large
$P_{M}(\mathbf{n})=\unicode[STIX]{x1D706}_{R_{\mathbf{0}}}(M_{\mathbf{n}})$
for all large
![]() $\mathbf{n}$
and
$\mathbf{n}$
and
![]() $e_{\unicode[STIX]{x1D6FC}}(M)\geqslant 0$
for all
$e_{\unicode[STIX]{x1D6FC}}(M)\geqslant 0$
for all
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
with
$\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
with
![]() $|\unicode[STIX]{x1D6FC}|=d-1$
.
$|\unicode[STIX]{x1D6FC}|=d-1$
.
Proposition 2.1. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
![]() $\mathbb{N}^{s}$
-graded ring defined over a local ring
$\mathbb{N}^{s}$
-graded ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
with infinite residue field
$(R_{\mathbf{0}},\mathfrak{m})$
with infinite residue field
![]() $R_{\mathbf{0}}/\mathfrak{m}$
. Let
$R_{\mathbf{0}}/\mathfrak{m}$
. Let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{N}^{s}$
-graded
$\mathbb{N}^{s}$
-graded
![]() $R$
-module, and let
$R$
-module, and let
![]() $\text{dim}\,M^{\unicode[STIX]{x1D6E5}}\geqslant 1$
. Fix
$\text{dim}\,M^{\unicode[STIX]{x1D6E5}}\geqslant 1$
. Fix
![]() $i\in \{1,\ldots ,s\}$
. If
$i\in \{1,\ldots ,s\}$
. If
![]() $R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
, then there exists
$R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
, then there exists
![]() $a\in R_{\mathbf{e}_{\mathbf{i}}}$
such that
$a\in R_{\mathbf{e}_{\mathbf{i}}}$
such that
![]() $a$
is
$a$
is
![]() $M$
-filter-regular.
$M$
-filter-regular.
Proof. Denote
![]() $M/H_{R_{++}}^{0}(M)$
by
$M/H_{R_{++}}^{0}(M)$
by
![]() $M^{\prime }$
. Then,
$M^{\prime }$
. Then,
Let
![]() $\text{Ass}(M^{\prime })=\{P_{1},\ldots ,P_{k}\}$
.
$\text{Ass}(M^{\prime })=\{P_{1},\ldots ,P_{k}\}$
.
Let
![]() $\mathfrak{a}_{i}$
be the ideal of
$\mathfrak{a}_{i}$
be the ideal of
![]() $R$
generated by
$R$
generated by
![]() $R_{\mathbf{e}_{\mathbf{i}}}$
. Therefore, for all
$R_{\mathbf{e}_{\mathbf{i}}}$
. Therefore, for all
![]() $j=1,\ldots ,k$
,
$j=1,\ldots ,k$
,
![]() $P_{j}\nsupseteq \mathfrak{a}_{i}$
. Consider the
$P_{j}\nsupseteq \mathfrak{a}_{i}$
. Consider the
![]() $R_{\mathbf{0}}/\mathfrak{m}$
-vector space
$R_{\mathbf{0}}/\mathfrak{m}$
-vector space
![]() $R_{\mathbf{e}_{\mathbf{i}}}/\mathfrak{m}R_{\mathbf{e}_{\mathbf{i}}}$
. Then, for each
$R_{\mathbf{e}_{\mathbf{i}}}/\mathfrak{m}R_{\mathbf{e}_{\mathbf{i}}}$
. Then, for each
![]() $j=1,\ldots ,k$
,
$j=1,\ldots ,k$
,
Since
![]() $R_{\mathbf{0}}/\mathfrak{m}$
is infinite, there exists
$R_{\mathbf{0}}/\mathfrak{m}$
is infinite, there exists
![]() $a\in R_{\mathbf{e}_{\mathbf{i}}}\setminus \bigcup _{j=1}^{k}(P_{j}\cap R_{\mathbf{e}_{\mathbf{i}}}+\mathfrak{m}R_{\mathbf{e}_{\mathbf{i}}})$
.
$a\in R_{\mathbf{e}_{\mathbf{i}}}\setminus \bigcup _{j=1}^{k}(P_{j}\cap R_{\mathbf{e}_{\mathbf{i}}}+\mathfrak{m}R_{\mathbf{e}_{\mathbf{i}}})$
.
By [Reference Masuti, Sarkar and Verma11, Proposition 4.1], there exists
![]() $\mathbf{m}$
such that
$\mathbf{m}$
such that
![]() $[H_{R_{++}}^{0}(M)]_{\mathbf{n}}=0$
for all
$[H_{R_{++}}^{0}(M)]_{\mathbf{n}}=0$
for all
![]() $\mathbf{n}\geqslant \mathbf{m}$
. Let
$\mathbf{n}\geqslant \mathbf{m}$
. Let
![]() $\mathbf{n}\geqslant \mathbf{m}$
, and let
$\mathbf{n}\geqslant \mathbf{m}$
, and let
![]() $x\in (0:_{M}a)_{\mathbf{n}}$
. Then,
$x\in (0:_{M}a)_{\mathbf{n}}$
. Then,
![]() $ax^{\prime }=0$
in
$ax^{\prime }=0$
in
![]() $M^{\prime }$
, where
$M^{\prime }$
, where
![]() $x^{\prime }$
is the image of
$x^{\prime }$
is the image of
![]() $x$
in
$x$
in
![]() $M^{\prime }$
. Since
$M^{\prime }$
. Since
![]() $a$
is a nonzero divisor of
$a$
is a nonzero divisor of
![]() $M^{\prime }$
,
$M^{\prime }$
,
![]() $x\in [H_{R_{++}}^{0}(M)]_{\mathbf{n}}=0$
.◻
$x\in [H_{R_{++}}^{0}(M)]_{\mathbf{n}}=0$
.◻
Proposition 2.2. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
![]() $\mathbb{N}^{s}$
-graded ring defined over an Artinian local ring
$\mathbb{N}^{s}$
-graded ring defined over an Artinian local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
. Let
$(R_{\mathbf{0}},\mathfrak{m})$
. Let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{N}^{s}$
-graded
$\mathbb{N}^{s}$
-graded
![]() $R$
-module. Let
$R$
-module. Let
![]() $a_{i}\in R_{\mathbf{e}_{\mathbf{i}}}$
be an
$a_{i}\in R_{\mathbf{e}_{\mathbf{i}}}$
be an
![]() $M$
-filter-regular element. Then, for all large
$M$
-filter-regular element. Then, for all large
![]() $\mathbf{n}$
,
$\mathbf{n}$
,
and hence for all
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
,
$\mathbf{n}\in \mathbb{Z}^{s}$
,
![]() $P_{M/a_{i}M}(\mathbf{n})=P_{M}(\mathbf{n})-P_{M}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})$
.
$P_{M/a_{i}M}(\mathbf{n})=P_{M}(\mathbf{n})-P_{M}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})$
.
Proof. Consider the exact sequence of
![]() $R_{0}$
-modules
$R_{0}$
-modules
Since
![]() $a_{i}$
is
$a_{i}$
is
![]() $M$
-filter-regular, for all large
$M$
-filter-regular, for all large
![]() $\mathbf{n}$
, we get
$\mathbf{n}$
, we get
and hence for all
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
,
$\mathbf{n}\in \mathbb{Z}^{s}$
,
![]() $P_{M/a_{i}M}(\mathbf{n})=P_{M}(\mathbf{n})-P_{M}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})$
.◻
$P_{M/a_{i}M}(\mathbf{n})=P_{M}(\mathbf{n})-P_{M}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})$
.◻
Theorem 2.3. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard Noetherian
![]() $\mathbb{N}^{s}$
-graded ring defined over an Artinian local ring
$\mathbb{N}^{s}$
-graded ring defined over an Artinian local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
with infinite residue field
$(R_{\mathbf{0}},\mathfrak{m})$
with infinite residue field
![]() $R_{\mathbf{0}}/\mathfrak{m}$
and
$R_{\mathbf{0}}/\mathfrak{m}$
and
![]() $R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
$R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
![]() $i=1,\ldots ,s$
. Let
$i=1,\ldots ,s$
. Let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{N}^{s}$
-graded
$\mathbb{N}^{s}$
-graded
![]() $R$
-module, and let
$R$
-module, and let
![]() $\text{dim}\,M^{\unicode[STIX]{x1D6E5}}\geqslant 1$
. Let
$\text{dim}\,M^{\unicode[STIX]{x1D6E5}}\geqslant 1$
. Let
![]() $e_{\unicode[STIX]{x1D6FC}}(M)>0$
for all
$e_{\unicode[STIX]{x1D6FC}}(M)>0$
for all
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
, such that
$\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
, such that
![]() $|\unicode[STIX]{x1D6FC}|=\text{dim}\,M^{\unicode[STIX]{x1D6E5}}-1$
. Then, for any
$|\unicode[STIX]{x1D6FC}|=\text{dim}\,M^{\unicode[STIX]{x1D6E5}}-1$
. Then, for any
![]() $\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
such that
$\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
such that
![]() $|\mathbf{q}|=\text{dim}\,M^{\unicode[STIX]{x1D6E5}}$
, there exist
$|\mathbf{q}|=\text{dim}\,M^{\unicode[STIX]{x1D6E5}}$
, there exist
![]() $a_{i1},\ldots ,a_{iq_{i}}\in R_{\mathbf{e}_{\mathbf{i}}}$
for all
$a_{i1},\ldots ,a_{iq_{i}}\in R_{\mathbf{e}_{\mathbf{i}}}$
for all
![]() $i=1,\ldots ,s$
, such that
$i=1,\ldots ,s$
, such that
![]() $a_{11},\ldots ,a_{1q_{1}},\ldots ,a_{s1},\ldots ,a_{sq_{s}}$
is an
$a_{11},\ldots ,a_{1q_{1}},\ldots ,a_{s1},\ldots ,a_{sq_{s}}$
is an
![]() $M$
-filter-regular sequence, and for all large
$M$
-filter-regular sequence, and for all large
![]() $\mathbf{n}$
,
$\mathbf{n}$
,
![]() $M_{\mathbf{n}}=\sum _{i=1}^{s}\sum _{j=1}^{q_{i}}a_{ij}M_{\mathbf{n}-\mathbf{e}_{\mathbf{i}}}$
.
$M_{\mathbf{n}}=\sum _{i=1}^{s}\sum _{j=1}^{q_{i}}a_{ij}M_{\mathbf{n}-\mathbf{e}_{\mathbf{i}}}$
.
Proof. We use induction on
![]() $\text{dim}\,M^{\unicode[STIX]{x1D6E5}}=l$
. Let
$\text{dim}\,M^{\unicode[STIX]{x1D6E5}}=l$
. Let
![]() $l=1$
. Then, by Proposition 2.1, for each
$l=1$
. Then, by Proposition 2.1, for each
![]() $i=1,\ldots ,s$
, there exists
$i=1,\ldots ,s$
, there exists
![]() $a_{i}\in R_{\mathbf{e}_{\mathbf{i}}}$
such that
$a_{i}\in R_{\mathbf{e}_{\mathbf{i}}}$
such that
![]() $a_{i}$
is
$a_{i}$
is
![]() $M$
-filter-regular. Since
$M$
-filter-regular. Since
![]() $l=1$
,
$l=1$
,
![]() $P_{M}(\mathbf{n})$
is polynomial of total degree zero. Therefore, by Proposition 2.2,
$P_{M}(\mathbf{n})$
is polynomial of total degree zero. Therefore, by Proposition 2.2,
![]() $\unicode[STIX]{x1D706}_{R_{\mathbf{0}}}(M_{\mathbf{n}}/a_{i}M_{\mathbf{n}-\mathbf{e}_{\mathbf{i}}})=0$
for all large
$\unicode[STIX]{x1D706}_{R_{\mathbf{0}}}(M_{\mathbf{n}}/a_{i}M_{\mathbf{n}-\mathbf{e}_{\mathbf{i}}})=0$
for all large
![]() $\mathbf{n}$
, and hence we get the required result. Suppose that
$\mathbf{n}$
, and hence we get the required result. Suppose that
![]() $l\geqslant 2$
and that the result is true for all finitely generated
$l\geqslant 2$
and that the result is true for all finitely generated
![]() $\mathbb{N}^{s}$
-graded
$\mathbb{N}^{s}$
-graded
![]() $R$
-modules
$R$
-modules
![]() $T$
such that
$T$
such that
![]() $1\leqslant \text{dim}\,T^{\unicode[STIX]{x1D6E5}}\leqslant l-1$
and
$1\leqslant \text{dim}\,T^{\unicode[STIX]{x1D6E5}}\leqslant l-1$
and
![]() $e_{\unicode[STIX]{x1D6FC}}(T)>0$
for all
$e_{\unicode[STIX]{x1D6FC}}(T)>0$
for all
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
such that
$\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
such that
![]() $|\unicode[STIX]{x1D6FC}|=\text{dim}\,T^{\unicode[STIX]{x1D6E5}}-1$
. Let
$|\unicode[STIX]{x1D6FC}|=\text{dim}\,T^{\unicode[STIX]{x1D6E5}}-1$
. Let
![]() $M$
be a finitely generated
$M$
be a finitely generated
![]() $\mathbb{N}^{s}$
-graded
$\mathbb{N}^{s}$
-graded
![]() $R$
-module such that
$R$
-module such that
![]() $\text{dim}\,M^{\unicode[STIX]{x1D6E5}}=l$
and
$\text{dim}\,M^{\unicode[STIX]{x1D6E5}}=l$
and
![]() $e_{\unicode[STIX]{x1D6FC}}(M)>0$
for all
$e_{\unicode[STIX]{x1D6FC}}(M)>0$
for all
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
such that
$\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
such that
![]() $|\unicode[STIX]{x1D6FC}|=l-1$
. Fix
$|\unicode[STIX]{x1D6FC}|=l-1$
. Fix
![]() $\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
such that
$\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
such that
![]() $|\mathbf{q}|=\text{dim}\,M^{\unicode[STIX]{x1D6E5}}$
. Let
$|\mathbf{q}|=\text{dim}\,M^{\unicode[STIX]{x1D6E5}}$
. Let
![]() $i=\min \{j\mid q_{j}\neq 0\}$
. By Proposition 2.1, there exists
$i=\min \{j\mid q_{j}\neq 0\}$
. By Proposition 2.1, there exists
![]() $a_{i1}\in R_{\mathbf{e}_{\mathbf{i}}}$
such that
$a_{i1}\in R_{\mathbf{e}_{\mathbf{i}}}$
such that
![]() $a_{i1}$
is an
$a_{i1}$
is an
![]() $M$
-filter-regular element. Let
$M$
-filter-regular element. Let
![]() $N=M/a_{i1}M$
. Since
$N=M/a_{i1}M$
. Since
![]() $e_{\unicode[STIX]{x1D6FC}}(M)>0$
for all
$e_{\unicode[STIX]{x1D6FC}}(M)>0$
for all
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
such that
$\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
such that
![]() $|\unicode[STIX]{x1D6FC}|=\text{dim}\,M^{\unicode[STIX]{x1D6E5}}-1$
, by Proposition 2.2,
$|\unicode[STIX]{x1D6FC}|=\text{dim}\,M^{\unicode[STIX]{x1D6E5}}-1$
, by Proposition 2.2,
![]() $P_{N}(\mathbf{n})$
is a polynomial of degree
$P_{N}(\mathbf{n})$
is a polynomial of degree
![]() $l-2$
, and hence
$l-2$
, and hence
![]() $\text{dim}\,N^{\unicode[STIX]{x1D6E5}}=l-1$
. Let
$\text{dim}\,N^{\unicode[STIX]{x1D6E5}}=l-1$
. Let
![]() $\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{s})\in \mathbb{N}^{s}$
such that
$\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{s})\in \mathbb{N}^{s}$
such that
![]() $|\unicode[STIX]{x1D6FD}|=l-2$
and
$|\unicode[STIX]{x1D6FD}|=l-2$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}+\mathbf{e}_{\mathbf{i}}$
. Then,
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}+\mathbf{e}_{\mathbf{i}}$
. Then,
![]() $e_{\unicode[STIX]{x1D6FD}}(N)=e_{\unicode[STIX]{x1D6FC}}(M)>0$
. Let
$e_{\unicode[STIX]{x1D6FD}}(N)=e_{\unicode[STIX]{x1D6FC}}(M)>0$
. Let
![]() $\mathbf{m}=\mathbf{q}-\mathbf{e}_{\mathbf{i}}\in \mathbb{N}^{s}$
; that is,
$\mathbf{m}=\mathbf{q}-\mathbf{e}_{\mathbf{i}}\in \mathbb{N}^{s}$
; that is,
![]() $m_{i}=q_{i}-1$
and for all
$m_{i}=q_{i}-1$
and for all
![]() $j\neq i$
,
$j\neq i$
,
![]() $m_{j}=q_{j}$
. Since
$m_{j}=q_{j}$
. Since
![]() $|\mathbf{m}|=l-1$
, by induction hypothesis there exist
$|\mathbf{m}|=l-1$
, by induction hypothesis there exist
![]() $b_{j1},\ldots ,b_{jm_{j}}\in R_{\mathbf{e}_{\mathbf{j}}}$
for all
$b_{j1},\ldots ,b_{jm_{j}}\in R_{\mathbf{e}_{\mathbf{j}}}$
for all
![]() $j=1,\ldots ,s$
such that
$j=1,\ldots ,s$
such that
![]() $b_{11},\ldots ,b_{1m_{1}},\ldots ,b_{s1},\ldots ,b_{sm_{s}}$
is an
$b_{11},\ldots ,b_{1m_{1}},\ldots ,b_{s1},\ldots ,b_{sm_{s}}$
is an
![]() $N$
-filter-regular sequence and for all large
$N$
-filter-regular sequence and for all large
![]() $\mathbf{n}$
,
$\mathbf{n}$
,
![]() $N_{\mathbf{n}}=\sum _{k=1}^{s}\sum _{j=1}^{m_{k}}b_{kj}N_{\mathbf{n}-\mathbf{e_{k}}}$
. Let
$N_{\mathbf{n}}=\sum _{k=1}^{s}\sum _{j=1}^{m_{k}}b_{kj}N_{\mathbf{n}-\mathbf{e_{k}}}$
. Let
![]() $a_{ik}=b_{i(k-1)}$
for all
$a_{ik}=b_{i(k-1)}$
for all
![]() $k=2,\ldots ,q_{i}$
and for all
$k=2,\ldots ,q_{i}$
and for all
![]() $j\neq i$
,
$j\neq i$
,
![]() $a_{jk}=b_{jk}$
for all
$a_{jk}=b_{jk}$
for all
![]() $k=1,\ldots ,q_{j}$
. Then, for all large
$k=1,\ldots ,q_{j}$
. Then, for all large
![]() $\mathbf{n}$
,
$\mathbf{n}$
,
![]() $M_{\mathbf{n}}=\sum _{i=1}^{s}\sum _{j=1}^{q_{i}}a_{ij}M_{\mathbf{n}-\mathbf{e}_{\mathbf{i}}}$
. Since
$M_{\mathbf{n}}=\sum _{i=1}^{s}\sum _{j=1}^{q_{i}}a_{ij}M_{\mathbf{n}-\mathbf{e}_{\mathbf{i}}}$
. Since
![]() $a_{i1}$
is
$a_{i1}$
is
![]() $M$
-filter-regular,
$M$
-filter-regular,
![]() $a_{11},\ldots ,a_{1q_{1}},\ldots ,a_{s1},\ldots ,a_{sq_{s}}$
is an
$a_{11},\ldots ,a_{1q_{1}},\ldots ,a_{s1},\ldots ,a_{sq_{s}}$
is an
![]() $M$
-filter-regular sequence.◻
$M$
-filter-regular sequence.◻
Theorem 2.4. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of dimension
$(R,\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d\geqslant 1$
, and let
$d\geqslant 1$
, and let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals in
$\mathfrak{m}$
-primary ideals in
![]() $R$
. Let
$R$
. Let
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
![]() $\mathbf{I}$
-admissible filtration of ideals in
$\mathbf{I}$
-admissible filtration of ideals in
![]() $R$
, and let
$R$
, and let
![]() $\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
, such that
$\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
, such that
![]() $|\mathbf{q}|=d$
. Then, there exists a joint reduction
$|\mathbf{q}|=d$
. Then, there exists a joint reduction
![]() $\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
of
$\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
of
![]() ${\mathcal{F}}$
of type
${\mathcal{F}}$
of type
![]() $\mathbf{q}$
such that
$\mathbf{q}$
such that
![]() $a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast }$
is a
$a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast }$
is a
![]() $G({\mathcal{F}})$
-filter-regular sequence, where
$G({\mathcal{F}})$
-filter-regular sequence, where
![]() $a_{ij}^{\ast }$
is the image of
$a_{ij}^{\ast }$
is the image of
![]() $a_{ij}$
in
$a_{ij}$
in
![]() $G(\mathbf{I})_{\mathbf{e}_{\mathbf{i}}}$
for all
$G(\mathbf{I})_{\mathbf{e}_{\mathbf{i}}}$
for all
![]() $j=1,\ldots ,q_{i}$
and
$j=1,\ldots ,q_{i}$
and
![]() $i=1,\ldots ,s$
.
$i=1,\ldots ,s$
.
Proof. Since
![]() ${\mathcal{F}}$
is an
${\mathcal{F}}$
is an
![]() $\mathbf{I}$
-admissible filtration,
$\mathbf{I}$
-admissible filtration,
![]() $G({\mathcal{F}})$
is a finitely generated
$G({\mathcal{F}})$
is a finitely generated
![]() $G(\mathbf{I})$
-module. By [Reference Rees12, Theorem 2.4], there exists a polynomial
$G(\mathbf{I})$
-module. By [Reference Rees12, Theorem 2.4], there exists a polynomial
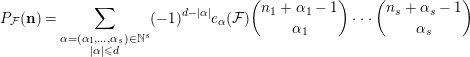 $$\begin{eqnarray}P_{{\mathcal{F}}}(\mathbf{n})=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{s})\in \mathbb{N}^{s} \\ |\unicode[STIX]{x1D6FC}|\leqslant d}}(-1)^{d-|\unicode[STIX]{x1D6FC}|}e_{\unicode[STIX]{x1D6FC}}({\mathcal{F}})\binom{n_{1}+\unicode[STIX]{x1D6FC}_{1}-1}{\unicode[STIX]{x1D6FC}_{1}}\cdots \binom{n_{s}+\unicode[STIX]{x1D6FC}_{s}-1}{\unicode[STIX]{x1D6FC}_{s}}\end{eqnarray}$$
$$\begin{eqnarray}P_{{\mathcal{F}}}(\mathbf{n})=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{s})\in \mathbb{N}^{s} \\ |\unicode[STIX]{x1D6FC}|\leqslant d}}(-1)^{d-|\unicode[STIX]{x1D6FC}|}e_{\unicode[STIX]{x1D6FC}}({\mathcal{F}})\binom{n_{1}+\unicode[STIX]{x1D6FC}_{1}-1}{\unicode[STIX]{x1D6FC}_{1}}\cdots \binom{n_{s}+\unicode[STIX]{x1D6FC}_{s}-1}{\unicode[STIX]{x1D6FC}_{s}}\end{eqnarray}$$
such that for all large
![]() $\mathbf{n}$
,
$\mathbf{n}$
,
![]() $P_{{\mathcal{F}}}(\mathbf{n})=\unicode[STIX]{x1D706}_{R}(R/{\mathcal{F}}(\mathbf{n}))$
,
$P_{{\mathcal{F}}}(\mathbf{n})=\unicode[STIX]{x1D706}_{R}(R/{\mathcal{F}}(\mathbf{n}))$
,
![]() $e_{\unicode[STIX]{x1D6FC}}({\mathcal{F}})\in \mathbb{Z}$
and
$e_{\unicode[STIX]{x1D6FC}}({\mathcal{F}})\in \mathbb{Z}$
and
![]() $e_{\unicode[STIX]{x1D6FC}}({\mathcal{F}})>0$
for all
$e_{\unicode[STIX]{x1D6FC}}({\mathcal{F}})>0$
for all
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
, where
$\unicode[STIX]{x1D6FC}\in \mathbb{N}^{s}$
, where
![]() $|\unicode[STIX]{x1D6FC}|=d$
. Hence,
$|\unicode[STIX]{x1D6FC}|=d$
. Hence,
is a numerical polynomial in
![]() $\mathbb{Q}[X_{1},\ldots ,X_{s}]$
of total degree
$\mathbb{Q}[X_{1},\ldots ,X_{s}]$
of total degree
![]() $d-1$
for all large
$d-1$
for all large
![]() $\mathbf{n}$
and
$\mathbf{n}$
and
![]() $e_{\unicode[STIX]{x1D6FD}}(G({\mathcal{F}}))>0$
for all
$e_{\unicode[STIX]{x1D6FD}}(G({\mathcal{F}}))>0$
for all
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{N}^{s}$
, where
$\unicode[STIX]{x1D6FD}\in \mathbb{N}^{s}$
, where
![]() $|\unicode[STIX]{x1D6FD}|=d-1$
. Therefore, by Theorem 2.3, there exist
$|\unicode[STIX]{x1D6FD}|=d-1$
. Therefore, by Theorem 2.3, there exist
![]() $a_{i1},\ldots ,a_{iq_{i}}\in I_{i}$
for all
$a_{i1},\ldots ,a_{iq_{i}}\in I_{i}$
for all
![]() $i=1,\ldots ,s$
, such that
$i=1,\ldots ,s$
, such that
![]() $a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast }$
is a
$a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast }$
is a
![]() $G({\mathcal{F}})$
-filter-regular sequence, where
$G({\mathcal{F}})$
-filter-regular sequence, where
![]() $a_{ij}^{\ast }=a_{ij}+\mathbf{I}^{\mathbf{e}+\mathbf{e}_{\mathbf{i}}}\in G(\mathbf{I})_{\mathbf{e}_{\mathbf{i}}}$
for all
$a_{ij}^{\ast }=a_{ij}+\mathbf{I}^{\mathbf{e}+\mathbf{e}_{\mathbf{i}}}\in G(\mathbf{I})_{\mathbf{e}_{\mathbf{i}}}$
for all
![]() $j=1,\ldots ,q_{i}$
,
$j=1,\ldots ,q_{i}$
,
![]() $i=1,\ldots ,s$
and
$i=1,\ldots ,s$
and
for all large
![]() $\mathbf{n}$
. Hence,
$\mathbf{n}$
. Hence,
Since
![]() ${\mathcal{F}}$
is an
${\mathcal{F}}$
is an
![]() $\mathbf{I}$
-admissible filtration, by [Reference Rees12], for each
$\mathbf{I}$
-admissible filtration, by [Reference Rees12], for each
![]() $i=1,\ldots ,s$
, there exists an integer
$i=1,\ldots ,s$
, there exists an integer
![]() $r_{i}$
such that for all
$r_{i}$
such that for all
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
, where
$\mathbf{n}\in \mathbb{Z}^{s}$
, where
![]() $n_{i}\geqslant r_{i}$
,
$n_{i}\geqslant r_{i}$
,
![]() ${\mathcal{F}}(\mathbf{n}+\mathbf{e}_{\mathbf{i}})=I_{i}{\mathcal{F}}(\mathbf{n})$
. Hence, for all large
${\mathcal{F}}(\mathbf{n}+\mathbf{e}_{\mathbf{i}})=I_{i}{\mathcal{F}}(\mathbf{n})$
. Hence, for all large
![]() $\mathbf{n}$
, we get
$\mathbf{n}$
, we get
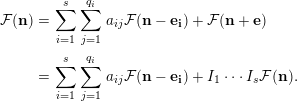 $$\begin{eqnarray}\displaystyle {\mathcal{F}}(\mathbf{n}) & = & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+\mathbf{e})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+I_{1}\cdots I_{s}{\mathcal{F}}(\mathbf{n}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}(\mathbf{n}) & = & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+\mathbf{e})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+I_{1}\cdots I_{s}{\mathcal{F}}(\mathbf{n}).\nonumber\end{eqnarray}$$
Thus, by Nakayama’s lemma, for all large
![]() $\mathbf{n}$
,
$\mathbf{n}$
,
3 Vanishing of local cohomology modules of Rees algebra of multigraded filtrations
Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
![]() $\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
$\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
, and let
$(R_{\mathbf{0}},\mathfrak{m})$
, and let
![]() $R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
$R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
![]() $i=1,\ldots ,s$
. For a nonempty subset
$i=1,\ldots ,s$
. For a nonempty subset
![]() $J$
of
$J$
of
![]() $\{1,\ldots ,s\}$
, we define
$\{1,\ldots ,s\}$
, we define
![]() ${\mathcal{M}}_{J}=\sum _{j\in J}{\mathcal{M}}_{j}$
.
${\mathcal{M}}_{J}=\sum _{j\in J}{\mathcal{M}}_{j}$
.
Lemma 3.1. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
![]() $\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
$\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
,
$(R_{\mathbf{0}},\mathfrak{m})$
,
![]() $R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
$R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
![]() $i=1,\ldots ,s$
, and let
$i=1,\ldots ,s$
, and let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{N}^{s}$
-graded
$\mathbb{N}^{s}$
-graded
![]() $R$
-module. Let
$R$
-module. Let
![]() $\mathbf{a}=(a_{1},\ldots ,a_{s})\in \mathbb{Z}^{s}$
, and let
$\mathbf{a}=(a_{1},\ldots ,a_{s})\in \mathbb{Z}^{s}$
, and let
![]() $J$
be any nonempty subset of
$J$
be any nonempty subset of
![]() $\{1,\ldots ,s\}$
. Suppose that
$\{1,\ldots ,s\}$
. Suppose that
![]() $[H_{{\mathcal{M}}}^{i}(M)]_{\mathbf{n}}=0$
for all
$[H_{{\mathcal{M}}}^{i}(M)]_{\mathbf{n}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
such that
$\mathbf{n}\in \mathbb{Z}^{s}$
such that
![]() $n_{k}>a_{k}$
for at least one
$n_{k}>a_{k}$
for at least one
![]() $k\in J$
. Then,
$k\in J$
. Then,
![]() $[H_{{\mathcal{M}}_{J}}^{i}(M)]_{\mathbf{n}}=0$
for all
$[H_{{\mathcal{M}}_{J}}^{i}(M)]_{\mathbf{n}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
such that
$\mathbf{n}\in \mathbb{Z}^{s}$
such that
![]() $\sum _{j\in J}n_{j}>\sum _{j\in J}a_{j}$
.
$\sum _{j\in J}n_{j}>\sum _{j\in J}a_{j}$
.
Proof. Consider a group homomorphism
![]() $\unicode[STIX]{x1D719}:\mathbb{Z}^{s}\rightarrow \mathbb{Z}$
defined by
$\unicode[STIX]{x1D719}:\mathbb{Z}^{s}\rightarrow \mathbb{Z}$
defined by
![]() $\unicode[STIX]{x1D719}(\mathbf{n})=\sum _{j\in J}n_{j}$
. Then,
$\unicode[STIX]{x1D719}(\mathbf{n})=\sum _{j\in J}n_{j}$
. Then,
![]() $R^{\unicode[STIX]{x1D719}}=\bigoplus _{n\geqslant 0} (\bigoplus _{\unicode[STIX]{x1D719}(\mathbf{n})=n}R_{\mathbf{n}} )$
. Let
$R^{\unicode[STIX]{x1D719}}=\bigoplus _{n\geqslant 0} (\bigoplus _{\unicode[STIX]{x1D719}(\mathbf{n})=n}R_{\mathbf{n}} )$
. Let
![]() $S=(R^{\unicode[STIX]{x1D719}})_{0}$
, and let
$S=(R^{\unicode[STIX]{x1D719}})_{0}$
, and let
![]() ${\mathcal{N}}$
be the maximal homogeneous ideal of
${\mathcal{N}}$
be the maximal homogeneous ideal of
![]() $S$
. Therefore,
$S$
. Therefore,
![]() $(R^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}$
is an
$(R^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}$
is an
![]() $\mathbb{N}$
-graded ring defined over the local ring
$\mathbb{N}$
-graded ring defined over the local ring
![]() $S_{{\mathcal{N}}}$
and
$S_{{\mathcal{N}}}$
and
![]() $(({\mathcal{M}}_{J})^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}$
is the irrelevant ideal of
$(({\mathcal{M}}_{J})^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}$
is the irrelevant ideal of
![]() $(R^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}$
. Then, for all
$(R^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}$
. Then, for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $m>\sum _{j\in J}a_{j}$
,
$m>\sum _{j\in J}a_{j}$
,
Since
![]() $m>\sum _{j\in J}a_{j}$
,
$m>\sum _{j\in J}a_{j}$
,
![]() $\unicode[STIX]{x1D719}(\mathbf{n})=m$
implies
$\unicode[STIX]{x1D719}(\mathbf{n})=m$
implies
![]() $n_{k}>a_{k}$
for at least one
$n_{k}>a_{k}$
for at least one
![]() $k\in J$
. Hence,
$k\in J$
. Hence,
![]() $[H_{({\mathcal{M}}^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}}^{i}(M_{{\mathcal{N}}}^{\unicode[STIX]{x1D719}})]_{m}=0$
for all
$[H_{({\mathcal{M}}^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}}^{i}(M_{{\mathcal{N}}}^{\unicode[STIX]{x1D719}})]_{m}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $m>\sum _{j\in J}a_{j}$
. Then, by Lemma 1.8, taking
$m>\sum _{j\in J}a_{j}$
. Then, by Lemma 1.8, taking
![]() $\mathfrak{a}=0$
we get
$\mathfrak{a}=0$
we get
![]() $[H_{(({\mathcal{M}}_{J})^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}}^{i}(M^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}]_{m}=0$
for all
$[H_{(({\mathcal{M}}_{J})^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}}^{i}(M^{\unicode[STIX]{x1D719}})_{{\mathcal{N}}}]_{m}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $m>\sum _{j\in J}a_{j}$
. Thus,
$m>\sum _{j\in J}a_{j}$
. Thus,
![]() $(\bigoplus _{\unicode[STIX]{x1D719}(\mathbf{n})=m}[H_{{\mathcal{M}}_{J}}^{i}(M)]_{\mathbf{n}} )\otimes _{S}S_{{\mathcal{N}}}=0$
for all
$(\bigoplus _{\unicode[STIX]{x1D719}(\mathbf{n})=m}[H_{{\mathcal{M}}_{J}}^{i}(M)]_{\mathbf{n}} )\otimes _{S}S_{{\mathcal{N}}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $m>\sum _{j\in J}a_{j}$
. Therefore,
$m>\sum _{j\in J}a_{j}$
. Therefore,
![]() $[H_{{\mathcal{M}}_{J}}^{i}(M)]_{\mathbf{n}}=0$
for all
$[H_{{\mathcal{M}}_{J}}^{i}(M)]_{\mathbf{n}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
such that
$\mathbf{n}\in \mathbb{Z}^{s}$
such that
![]() $\sum _{j\in J}n_{j}>\sum _{j\in J}a_{j}$
.◻
$\sum _{j\in J}n_{j}>\sum _{j\in J}a_{j}$
.◻
Proposition 3.2. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
![]() $\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
$\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
,
$(R_{\mathbf{0}},\mathfrak{m})$
,
![]() $R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
$R_{\mathbf{e}_{\mathbf{i}}}\neq 0$
for all
![]() $i=1,\ldots ,s$
, and let
$i=1,\ldots ,s$
, and let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{N}^{s}$
-graded
$\mathbb{N}^{s}$
-graded
![]() $R$
-module. Let
$R$
-module. Let
![]() $I$
be any subset of
$I$
be any subset of
![]() $\{1,\ldots ,s\}$
, and let
$\{1,\ldots ,s\}$
, and let
![]() $J$
be a nonempty subset of
$J$
be a nonempty subset of
![]() $\{1,\ldots ,s\}$
, such that
$\{1,\ldots ,s\}$
, such that
![]() $I$
and
$I$
and
![]() $J$
are disjoint. Suppose that
$J$
are disjoint. Suppose that
![]() $\mathbf{a}=(a_{1},\ldots ,a_{s})\in \mathbb{Z}^{s}$
and
$\mathbf{a}=(a_{1},\ldots ,a_{s})\in \mathbb{Z}^{s}$
and
![]() $[H_{{\mathcal{M}}}^{i}(M)]_{\mathbf{n}}=0$
for all
$[H_{{\mathcal{M}}}^{i}(M)]_{\mathbf{n}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
such that
$\mathbf{n}\in \mathbb{Z}^{s}$
such that
![]() $n_{k}>a_{k}$
for at least one
$n_{k}>a_{k}$
for at least one
![]() $k\in \{1,\ldots ,s\}$
. Then,
$k\in \{1,\ldots ,s\}$
. Then,
![]() $[H_{{\mathcal{M}}_{I,J}}^{i}(M)]_{\mathbf{n}}=0$
for all
$[H_{{\mathcal{M}}_{I,J}}^{i}(M)]_{\mathbf{n}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\geqslant \mathbf{a}+\mathbf{e}$
. In particular,
$\mathbf{n}\geqslant \mathbf{a}+\mathbf{e}$
. In particular,
![]() $M$
satisfies Hyry’s condition
$M$
satisfies Hyry’s condition
![]() $\text{H}_{R}(M,\mathbf{a}+\mathbf{e})$
.
$\text{H}_{R}(M,\mathbf{a}+\mathbf{e})$
.
Proof. We follow the argument given in [Reference Tài Hà6, Theorem 3.2.6] and use induction on
![]() $r=|I\cup J|$
. Suppose that
$r=|I\cup J|$
. Suppose that
![]() $r=1$
. Since
$r=1$
. Since
![]() $I,J$
are disjoint and
$I,J$
are disjoint and
![]() $|J|\geqslant 1$
, we have
$|J|\geqslant 1$
, we have
![]() $I=\emptyset$
, and the result follows from Lemma 3.1. Suppose that
$I=\emptyset$
, and the result follows from Lemma 3.1. Suppose that
![]() $r\geqslant 2$
and the result is true up to
$r\geqslant 2$
and the result is true up to
![]() $r-1$
. Let
$r-1$
. Let
![]() $I=\{i_{1},\ldots ,i_{k}\}$
, and let
$I=\{i_{1},\ldots ,i_{k}\}$
, and let
![]() $J=\{i_{k+1},\ldots ,i_{r}\}$
. We use induction on
$J=\{i_{k+1},\ldots ,i_{r}\}$
. We use induction on
![]() $k$
. If
$k$
. If
![]() $k=0$
, then, again by Lemma 3.1, we get the result. Suppose that
$k=0$
, then, again by Lemma 3.1, we get the result. Suppose that
![]() $k\geqslant 1$
and the result is true up to
$k\geqslant 1$
and the result is true up to
![]() $k-1$
. Let
$k-1$
. Let
![]() ${\mathcal{I}}=I\setminus \{i_{k}\}$
, and let
${\mathcal{I}}=I\setminus \{i_{k}\}$
, and let
![]() ${\mathcal{J}}=J\cup \{i_{k}\}$
. Then,
${\mathcal{J}}=J\cup \{i_{k}\}$
. Then,
![]() ${\mathcal{M}}_{{\mathcal{I}},J}+{\mathcal{M}}_{{\mathcal{I}},\{i_{k}\}}={\mathcal{M}}_{{\mathcal{I}},{\mathcal{J}}}$
and
${\mathcal{M}}_{{\mathcal{I}},J}+{\mathcal{M}}_{{\mathcal{I}},\{i_{k}\}}={\mathcal{M}}_{{\mathcal{I}},{\mathcal{J}}}$
and
![]() ${\mathcal{M}}_{{\mathcal{I}},J}\cap {\mathcal{M}}_{{\mathcal{I}},\{i_{k}\}}={\mathcal{M}}_{I,J}$
. Consider the following Mayer–Vietoris sequence of local cohomology modules:
${\mathcal{M}}_{{\mathcal{I}},J}\cap {\mathcal{M}}_{{\mathcal{I}},\{i_{k}\}}={\mathcal{M}}_{I,J}$
. Consider the following Mayer–Vietoris sequence of local cohomology modules:
Using induction on
![]() $k$
, we get
$k$
, we get
![]() $[H_{{\mathcal{M}}_{{\mathcal{I}},{\mathcal{J}}}}^{i+1}(M)]_{\mathbf{n}}=0$
for all
$[H_{{\mathcal{M}}_{{\mathcal{I}},{\mathcal{J}}}}^{i+1}(M)]_{\mathbf{n}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\geqslant \mathbf{a}+\mathbf{e}$
, and using induction on
$\mathbf{n}\geqslant \mathbf{a}+\mathbf{e}$
, and using induction on
![]() $r$
, we get
$r$
, we get
![]() $[H_{{\mathcal{M}}_{{\mathcal{I}},J}}^{i}(M)]_{\mathbf{n}}=0=[H_{{\mathcal{M}}_{{\mathcal{I}},\{i_{k}\}}}^{i}(M)]_{\boldsymbol{ n}}$
for all
$[H_{{\mathcal{M}}_{{\mathcal{I}},J}}^{i}(M)]_{\mathbf{n}}=0=[H_{{\mathcal{M}}_{{\mathcal{I}},\{i_{k}\}}}^{i}(M)]_{\boldsymbol{ n}}$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\geqslant \mathbf{a}+\mathbf{e}$
. For
$\mathbf{n}\geqslant \mathbf{a}+\mathbf{e}$
. For
![]() $R_{++}$
, we take
$R_{++}$
, we take
![]() $I=\{1,\ldots ,s-1\}$
and
$I=\{1,\ldots ,s-1\}$
and
![]() $J=\{s\}$
.◻
$J=\{s\}$
.◻
Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
![]() $\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
$\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
, and let
$(R_{\mathbf{0}},\mathfrak{m})$
, and let
![]() ${\mathcal{M}}$
be the maximal homogeneous ideal of
${\mathcal{M}}$
be the maximal homogeneous ideal of
![]() $R$
. Let
$R$
. Let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{Z}^{s}$
-graded
$\mathbb{Z}^{s}$
-graded
![]() $R$
-module. For all
$R$
-module. For all
![]() $i=1,\ldots ,s$
, define the
$i=1,\ldots ,s$
, define the
![]() $a$
-invariants of
$a$
-invariants of
![]() $M$
as
$M$
as
(see [Reference Hyry7]). Put
![]() $a(M)=(a^{1}(M),\ldots ,a^{s}(M))$
. We recall the following result.
$a(M)=(a^{1}(M),\ldots ,a^{s}(M))$
. We recall the following result.
Proposition 3.3. [Reference Masuti, Puthenpurakal and Verma10, Lemma 3.7]
Let
![]() $(R,\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
$(R,\mathfrak{m})$
be a Cohen–Macaulay local ring of dimension
![]() $d$
, let
$d$
, let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals of
$\mathfrak{m}$
-primary ideals of
![]() $R$
, and let
$R$
, and let
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
![]() $\mathbf{I}$
-admissible filtration of ideals in
$\mathbf{I}$
-admissible filtration of ideals in
![]() $R$
. Then,
$R$
. Then,
![]() $a({\mathcal{R}}({\mathcal{F}}))=-\mathbf{e}$
.
$a({\mathcal{R}}({\mathcal{F}}))=-\mathbf{e}$
.
Remark 3.4. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of dimension
$(R,\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d$
, and let
$d$
, and let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals in
$\mathfrak{m}$
-primary ideals in
![]() $R$
. Let
$R$
. Let
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
![]() $\mathbf{I}$
-admissible filtration of ideals in
$\mathbf{I}$
-admissible filtration of ideals in
![]() $R$
, and let
$R$
, and let
![]() ${\mathcal{R}}({\mathcal{F}})$
be Cohen–Macaulay. Then, by Propositions 3.3 and 3.2,
${\mathcal{R}}({\mathcal{F}})$
be Cohen–Macaulay. Then, by Propositions 3.3 and 3.2,
![]() ${\mathcal{R}}({\mathcal{F}})$
satisfies Hyry’s condition
${\mathcal{R}}({\mathcal{F}})$
satisfies Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
.
$\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
.
The next theorem is a generalization of a result due to Hyry [Reference Hyry8, Theorem 6.1] for
![]() $\mathbb{Z}^{s}$
-graded admissible filtration of ideals.
$\mathbb{Z}^{s}$
-graded admissible filtration of ideals.
Theorem 3.5. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of dimension
$(R,\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d$
, and let
$d$
, and let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals in
$\mathfrak{m}$
-primary ideals in
![]() $R$
. Let
$R$
. Let
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
![]() $\mathbf{I}$
-admissible filtration of ideals in
$\mathbf{I}$
-admissible filtration of ideals in
![]() $R$
, and let
$R$
, and let
![]() ${\mathcal{R}}({\mathcal{F}})$
satisfy Hyry’s condition
${\mathcal{R}}({\mathcal{F}})$
satisfy Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
. Then,
$\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
. Then,
-
(1)
 $P_{{\mathcal{F}}}(\mathbf{n})=H_{{\mathcal{F}}}(\mathbf{n})$
for all
$P_{{\mathcal{F}}}(\mathbf{n})=H_{{\mathcal{F}}}(\mathbf{n})$
for all
 $\mathbf{n}\in \mathbb{N}^{s}$
,
$\mathbf{n}\in \mathbb{N}^{s}$
, -
(2) for all
 $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{s})\in \mathbb{N}^{s}$
such that
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{s})\in \mathbb{N}^{s}$
such that
 $|\unicode[STIX]{x1D6FC}|=d$
, where
$|\unicode[STIX]{x1D6FC}|=d$
, where $$\begin{eqnarray}e_{\unicode[STIX]{x1D6FC}}({\mathcal{F}})=\mathop{\sum }_{n_{1}=0}^{\unicode[STIX]{x1D6FC}_{1}}\cdots \mathop{\sum }_{n_{s}=0}^{\unicode[STIX]{x1D6FC}_{s}}\binom{\unicode[STIX]{x1D6FC}_{1}}{n_{1}}\cdots \binom{\unicode[STIX]{x1D6FC}_{s}}{n_{s}}(-1)^{d-n_{1}-\cdots -n_{s}}\unicode[STIX]{x1D706}\left(\frac{R}{{\mathcal{F}}(\mathbf{n})}\right),\end{eqnarray}$$
$$\begin{eqnarray}e_{\unicode[STIX]{x1D6FC}}({\mathcal{F}})=\mathop{\sum }_{n_{1}=0}^{\unicode[STIX]{x1D6FC}_{1}}\cdots \mathop{\sum }_{n_{s}=0}^{\unicode[STIX]{x1D6FC}_{s}}\binom{\unicode[STIX]{x1D6FC}_{1}}{n_{1}}\cdots \binom{\unicode[STIX]{x1D6FC}_{s}}{n_{s}}(-1)^{d-n_{1}-\cdots -n_{s}}\unicode[STIX]{x1D706}\left(\frac{R}{{\mathcal{F}}(\mathbf{n})}\right),\end{eqnarray}$$
 $\mathbf{n}=(n_{1},\ldots ,n_{s})$
.
$\mathbf{n}=(n_{1},\ldots ,n_{s})$
.
Proof.
![]() $(1)$
Since
$(1)$
Since
![]() ${\mathcal{R}}({\mathcal{F}})$
satisfies Hyry’s condition
${\mathcal{R}}({\mathcal{F}})$
satisfies Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
, by [Reference Masuti, Sarkar and Verma11, Theorem 4.3], we get
$\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
, by [Reference Masuti, Sarkar and Verma11, Theorem 4.3], we get
![]() $P_{{\mathcal{F}}}(\mathbf{n})=H_{{\mathcal{F}}}(\mathbf{n})$
for all
$P_{{\mathcal{F}}}(\mathbf{n})=H_{{\mathcal{F}}}(\mathbf{n})$
for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
.
$\mathbf{n}\in \mathbb{N}^{s}$
.
![]() $(2)$
Consider the operators
$(2)$
Consider the operators
![]() $(\unicode[STIX]{x1D6E5}_{i}^{1}P_{{\mathcal{F}}})(\mathbf{n})=P_{{\mathcal{F}}}(\mathbf{n}+\mathbf{e}_{\mathbf{i}})-P_{{\mathcal{F}}}(\mathbf{n})$
for all
$(\unicode[STIX]{x1D6E5}_{i}^{1}P_{{\mathcal{F}}})(\mathbf{n})=P_{{\mathcal{F}}}(\mathbf{n}+\mathbf{e}_{\mathbf{i}})-P_{{\mathcal{F}}}(\mathbf{n})$
for all
![]() $i=1,\ldots ,s$
. Then,
$i=1,\ldots ,s$
. Then,
![]() $(\unicode[STIX]{x1D6E5}_{s}^{\unicode[STIX]{x1D6FC}_{s}}\cdots \unicode[STIX]{x1D6E5}_{1}^{\unicode[STIX]{x1D6FC}_{1}}P_{{\mathcal{F}}})(\mathbf{0})=e_{\unicode[STIX]{x1D6FC}}({\mathcal{F}})$
for
$(\unicode[STIX]{x1D6E5}_{s}^{\unicode[STIX]{x1D6FC}_{s}}\cdots \unicode[STIX]{x1D6E5}_{1}^{\unicode[STIX]{x1D6FC}_{1}}P_{{\mathcal{F}}})(\mathbf{0})=e_{\unicode[STIX]{x1D6FC}}({\mathcal{F}})$
for
![]() $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{s})\in \mathbb{N}^{s}$
,
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{s})\in \mathbb{N}^{s}$
,
![]() $|\unicode[STIX]{x1D6FC}|=d$
. By [Reference Snapper14, Proposition 1.2],
$|\unicode[STIX]{x1D6FC}|=d$
. By [Reference Snapper14, Proposition 1.2],
where
![]() $\mathbf{n}=(n_{1},\ldots ,n_{s})$
. Thus, from part
$\mathbf{n}=(n_{1},\ldots ,n_{s})$
. Thus, from part
![]() $(1)$
we get the required result.◻
$(1)$
we get the required result.◻
Lemma 3.6. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
![]() $\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
$\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
, and let
$(R_{\mathbf{0}},\mathfrak{m})$
, and let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{Z}^{s}$
-graded
$\mathbb{Z}^{s}$
-graded
![]() $R$
-module. Let
$R$
-module. Let
![]() $a\in R_{\mathbf{m}}$
be an
$a\in R_{\mathbf{m}}$
be an
![]() $M$
-filter-regular, where
$M$
-filter-regular, where
![]() $\mathbf{m}\neq \mathbf{0}$
. Then, for all
$\mathbf{m}\neq \mathbf{0}$
. Then, for all
![]() $\mathbf{n}\in \mathbb{Z}^{s}$
and
$\mathbf{n}\in \mathbb{Z}^{s}$
and
![]() $i\geqslant 0$
, the following sequence is exact:
$i\geqslant 0$
, the following sequence is exact:
Proof. Consider the following short exact sequence of
![]() $R$
-modules:
$R$
-modules:
Since
![]() $a$
is
$a$
is
![]() $M$
-filter-regular,
$M$
-filter-regular,
![]() $(0:_{M}a)$
is
$(0:_{M}a)$
is
![]() $R_{++}$
-torsion. Hence,
$R_{++}$
-torsion. Hence,
Therefore, the short exact sequence of
![]() $R$
-modules
$R$
-modules
gives the desired exact sequence. ◻
Lemma 3.7. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
![]() $\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
$\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
, and let
$(R_{\mathbf{0}},\mathfrak{m})$
, and let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{Z}^{s}$
-graded
$\mathbb{Z}^{s}$
-graded
![]() $R$
-module. Suppose that
$R$
-module. Suppose that
![]() $M$
satisfies Hyry’s condition
$M$
satisfies Hyry’s condition
![]() $\text{H}_{R}(M,\mathbf{m})$
. Let
$\text{H}_{R}(M,\mathbf{m})$
. Let
![]() $a_{1},\ldots ,a_{l}\in R_{\mathbf{e}_{\mathbf{j}}}$
be an
$a_{1},\ldots ,a_{l}\in R_{\mathbf{e}_{\mathbf{j}}}$
be an
![]() $M$
-filter-regular sequence. Then,
$M$
-filter-regular sequence. Then,
![]() $M/(a_{1},\ldots ,a_{l})M$
satisfies Hyry’s condition
$M/(a_{1},\ldots ,a_{l})M$
satisfies Hyry’s condition
![]() $\text{H}_{R}(M/(a_{1},\ldots ,a_{l})M,\mathbf{m}+l\mathbf{e}_{\mathbf{j}})$
.
$\text{H}_{R}(M/(a_{1},\ldots ,a_{l})M,\mathbf{m}+l\mathbf{e}_{\mathbf{j}})$
.
Proof. We use induction on
![]() $l$
. Let
$l$
. Let
![]() $l=1$
. By Lemma 3.6, for all
$l=1$
. By Lemma 3.6, for all
![]() $i\geqslant 0$
, we get the exact sequence
$i\geqslant 0$
, we get the exact sequence
Since for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\geqslant \mathbf{m}$
,
$\mathbf{n}\geqslant \mathbf{m}$
,
![]() $[H_{R_{++}}^{i}(M)]_{\mathbf{n}}=0$
, we get
$[H_{R_{++}}^{i}(M)]_{\mathbf{n}}=0$
, we get
![]() $\left[H_{R_{++}}^{i}\left(\frac{M}{a_{1}M}\right)\right]_{\mathbf{n}}=0$
for all
$\left[H_{R_{++}}^{i}\left(\frac{M}{a_{1}M}\right)\right]_{\mathbf{n}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\geqslant \mathbf{m}+\mathbf{e}_{\mathbf{j}}$
. Hence, the result is true for
$\mathbf{n}\geqslant \mathbf{m}+\mathbf{e}_{\mathbf{j}}$
. Hence, the result is true for
![]() $l=1$
.
$l=1$
.
Suppose that
![]() $l\geqslant 2$
and the result is true up to
$l\geqslant 2$
and the result is true up to
![]() $l-1$
. Let
$l-1$
. Let
![]() $N=M/(a_{1},\ldots ,a_{l-1})M$
. Then,
$N=M/(a_{1},\ldots ,a_{l-1})M$
. Then,
Since
![]() $a_{l}$
is
$a_{l}$
is
![]() $N$
-filter-regular, using the
$N$
-filter-regular, using the
![]() $l=1$
case, we get
$l=1$
case, we get
![]() $\left[H_{R_{++}}^{i}\left(\frac{N}{a_{l}N}\right)\right]_{\mathbf{n}}=0$
for all
$\left[H_{R_{++}}^{i}\left(\frac{N}{a_{l}N}\right)\right]_{\mathbf{n}}=0$
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\geqslant \mathbf{m}+l\mathbf{e}_{\mathbf{j}}$
.◻
$\mathbf{n}\geqslant \mathbf{m}+l\mathbf{e}_{\mathbf{j}}$
.◻
Proposition 3.8. Let
![]() $R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
$R=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}R_{\mathbf{n}}$
be a standard
![]() $\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
$\mathbb{N}^{s}$
-graded Noetherian ring defined over a local ring
![]() $(R_{\mathbf{0}},\mathfrak{m})$
, let
$(R_{\mathbf{0}},\mathfrak{m})$
, let
![]() $M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finitely generated
$M=\bigoplus _{\mathbf{n}\in \mathbb{Z}^{s}}M_{\mathbf{n}}$
be a finitely generated
![]() $\mathbb{Z}^{s}$
-graded
$\mathbb{Z}^{s}$
-graded
![]() $R$
-module, and let
$R$
-module, and let
![]() $M$
satisfy Hyry’s condition
$M$
satisfy Hyry’s condition
![]() $\text{H}_{R}(M,\mathbf{m})$
. Let
$\text{H}_{R}(M,\mathbf{m})$
. Let
![]() $\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
, let
$\mathbf{q}=(q_{1},\ldots ,q_{s})\in \mathbb{N}^{s}$
, let
![]() $a_{j1},\ldots ,a_{jq_{j}}\in R_{\mathbf{e}_{\mathbf{j}}}$
for all
$a_{j1},\ldots ,a_{jq_{j}}\in R_{\mathbf{e}_{\mathbf{j}}}$
for all
![]() $j=1,\ldots ,s$
such that
$j=1,\ldots ,s$
such that
![]() $a_{11},\ldots ,a_{1q_{1}},\ldots ,a_{s1},\ldots ,a_{sq_{s}}$
is an
$a_{11},\ldots ,a_{1q_{1}},\ldots ,a_{s1},\ldots ,a_{sq_{s}}$
is an
![]() $M$
-filter-regular sequence, and let
$M$
-filter-regular sequence, and let
![]() $N=M/(a_{11},\ldots ,a_{1q_{1}},\ldots ,a_{s1},\ldots ,a_{sq_{s}})M$
. Then,
$N=M/(a_{11},\ldots ,a_{1q_{1}},\ldots ,a_{s1},\ldots ,a_{sq_{s}})M$
. Then,
![]() $N$
satisfies Hyry’s condition
$N$
satisfies Hyry’s condition
![]() $\text{H}_{R}(N,\mathbf{m}+\mathbf{q})$
.
$\text{H}_{R}(N,\mathbf{m}+\mathbf{q})$
.
Proof. Define
![]() $N_{0}=M$
and
$N_{0}=M$
and
![]() $N_{j}=N_{j-1}/(a_{j1},\ldots ,a_{jq_{j}})N_{j-1}$
for all
$N_{j}=N_{j-1}/(a_{j1},\ldots ,a_{jq_{j}})N_{j-1}$
for all
![]() $j=1,\ldots ,s$
. Since
$j=1,\ldots ,s$
. Since
![]() $a_{j1},\ldots ,a_{jq_{j}}\in R_{\mathbf{e}_{\mathbf{j}}}$
is an
$a_{j1},\ldots ,a_{jq_{j}}\in R_{\mathbf{e}_{\mathbf{j}}}$
is an
![]() $N_{j-1}$
-filter-regular sequence for all
$N_{j-1}$
-filter-regular sequence for all
![]() $j=1,\ldots ,s$
, by Lemma 3.7, we get the required result.◻
$j=1,\ldots ,s$
, by Lemma 3.7, we get the required result.◻
Theorem 3.9. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of dimension
$(R,\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d\geqslant 1$
, and let
$d\geqslant 1$
, and let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals in
$\mathfrak{m}$
-primary ideals in
![]() $R$
. Let
$R$
. Let
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
![]() $\mathbf{I}$
-admissible filtration of ideals in
$\mathbf{I}$
-admissible filtration of ideals in
![]() $R$
. Suppose that
$R$
. Suppose that
![]() $G({\mathcal{F}})$
satisfies Hyry’s condition
$G({\mathcal{F}})$
satisfies Hyry’s condition
![]() $\text{H}_{G(\mathbf{I})}(G({\mathcal{F}}),\mathbf{m})$
. Let
$\text{H}_{G(\mathbf{I})}(G({\mathcal{F}}),\mathbf{m})$
. Let
![]() $\mathbf{q}\in \mathbb{N}^{s}$
such that
$\mathbf{q}\in \mathbb{N}^{s}$
such that
![]() $|\mathbf{q}|=d$
, and let
$|\mathbf{q}|=d$
, and let
![]() $\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
be a joint reduction of
$\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
be a joint reduction of
![]() ${\mathcal{F}}$
of type
${\mathcal{F}}$
of type
![]() $\mathbf{q}$
such that
$\mathbf{q}$
such that
![]() $a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast }$
is a
$a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast }$
is a
![]() $G({\mathcal{F}})$
-filter-regular sequence, where
$G({\mathcal{F}})$
-filter-regular sequence, where
![]() $a_{ij}^{\ast }$
is the image of
$a_{ij}^{\ast }$
is the image of
![]() $a_{ij}$
in
$a_{ij}$
in
![]() $G(\mathbf{I})_{\mathbf{e}_{\mathbf{i}}}$
for all
$G(\mathbf{I})_{\mathbf{e}_{\mathbf{i}}}$
for all
![]() $j=1,\ldots ,q_{i}$
and
$j=1,\ldots ,q_{i}$
and
![]() $i=1,\ldots ,s$
. Then,
$i=1,\ldots ,s$
. Then,
Proof. By Proposition 3.8, we get
for all
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $\mathbf{n}\geqslant \mathbf{m}+\mathbf{q}$
. Since
$\mathbf{n}\geqslant \mathbf{m}+\mathbf{q}$
. Since
![]() $\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
is a joint reduction of
$\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
is a joint reduction of
![]() ${\mathcal{F}}$
,
${\mathcal{F}}$
,
![]() $G({\mathcal{F}})/(a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast })G({\mathcal{F}})$
is
$G({\mathcal{F}})/(a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast })G({\mathcal{F}})$
is
![]() $G(\mathbf{I})_{++}$
-torsion. Thus,
$G(\mathbf{I})_{++}$
-torsion. Thus,
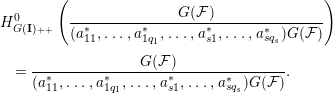 $$\begin{eqnarray}\displaystyle & & \displaystyle H_{G(\mathbf{I})_{++}}^{0}\left(\frac{G({\mathcal{F}})}{(a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast })G({\mathcal{F}})}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{G({\mathcal{F}})}{(a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast })G({\mathcal{F}})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle H_{G(\mathbf{I})_{++}}^{0}\left(\frac{G({\mathcal{F}})}{(a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast })G({\mathcal{F}})}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{G({\mathcal{F}})}{(a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast })G({\mathcal{F}})}.\nonumber\end{eqnarray}$$
Hence, for all
![]() $\mathbf{n}\geqslant \mathbf{m}+\mathbf{q}$
, we have
$\mathbf{n}\geqslant \mathbf{m}+\mathbf{q}$
, we have
Now, for all
![]() $k\geqslant 0$
and
$k\geqslant 0$
and
![]() $\mathbf{n}\geqslant \mathbf{m}+\mathbf{q}$
,
$\mathbf{n}\geqslant \mathbf{m}+\mathbf{q}$
,
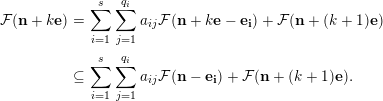 $$\begin{eqnarray}\displaystyle {\mathcal{F}}(\mathbf{n}+k\mathbf{e}) & = & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}+k\mathbf{e}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+(k+1)\mathbf{e})\nonumber\\ \displaystyle & \subseteq & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+(k+1)\mathbf{e}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}(\mathbf{n}+k\mathbf{e}) & = & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}+k\mathbf{e}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+(k+1)\mathbf{e})\nonumber\\ \displaystyle & \subseteq & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+(k+1)\mathbf{e}).\nonumber\end{eqnarray}$$
Since
![]() ${\mathcal{F}}$
is an
${\mathcal{F}}$
is an
![]() $\mathbf{I}$
-admissible filtration, by [Reference Rees12], for each
$\mathbf{I}$
-admissible filtration, by [Reference Rees12], for each
![]() $i=1,\ldots ,s$
, there exists integer
$i=1,\ldots ,s$
, there exists integer
![]() $r_{i}\in \mathbb{N}$
such that for all
$r_{i}\in \mathbb{N}$
such that for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
, where
$\mathbf{n}\in \mathbb{N}^{s}$
, where
![]() $n_{i}\geqslant r_{i}$
, we have
$n_{i}\geqslant r_{i}$
, we have
![]() ${\mathcal{F}}(\mathbf{n}+\mathbf{e}_{\mathbf{i}})=I_{i}{\mathcal{F}}(\mathbf{n})$
. Let
${\mathcal{F}}(\mathbf{n}+\mathbf{e}_{\mathbf{i}})=I_{i}{\mathcal{F}}(\mathbf{n})$
. Let
![]() $r=\max \{r_{i}:i=1,\ldots ,s\}$
. Therefore,
$r=\max \{r_{i}:i=1,\ldots ,s\}$
. Therefore,
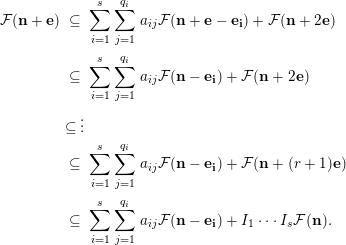 $$\begin{eqnarray}\displaystyle {\mathcal{F}}(\mathbf{n}+\mathbf{e}) & \subseteq & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}+\mathbf{e}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+2\mathbf{e})\nonumber\\ \displaystyle & \subseteq & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+2\mathbf{e})\nonumber\\ \displaystyle & \subseteq \vdots & \displaystyle \nonumber\\ \displaystyle & \subseteq & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+(r+1)\mathbf{e})\nonumber\\ \displaystyle & \subseteq & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+I_{1}\cdots I_{s}{\mathcal{F}}(\mathbf{n}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}(\mathbf{n}+\mathbf{e}) & \subseteq & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}+\mathbf{e}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+2\mathbf{e})\nonumber\\ \displaystyle & \subseteq & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+2\mathbf{e})\nonumber\\ \displaystyle & \subseteq \vdots & \displaystyle \nonumber\\ \displaystyle & \subseteq & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+{\mathcal{F}}(\mathbf{n}+(r+1)\mathbf{e})\nonumber\\ \displaystyle & \subseteq & \displaystyle \mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})+I_{1}\cdots I_{s}{\mathcal{F}}(\mathbf{n}).\nonumber\end{eqnarray}$$
Hence, by using Nakayama’s lemma, from the equality (3.9.1) we get the required result.◻
Lemma 3.10. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of dimension
$(R,\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d\geqslant 1$
, and let
$d\geqslant 1$
, and let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals in
$\mathfrak{m}$
-primary ideals in
![]() $R$
. Let
$R$
. Let
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
![]() $\mathbf{I}$
-admissible filtration of ideals in
$\mathbf{I}$
-admissible filtration of ideals in
![]() $R$
. Suppose that
$R$
. Suppose that
![]() ${\mathcal{R}}({\mathcal{F}})$
satisfies Hyry’s condition
${\mathcal{R}}({\mathcal{F}})$
satisfies Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{m})$
, where
$\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{m})$
, where
![]() $\mathbf{m}\in \mathbb{N}^{s}$
. Then,
$\mathbf{m}\in \mathbb{N}^{s}$
. Then,
![]() $G({\mathcal{F}})$
satisfies Hyry’s condition
$G({\mathcal{F}})$
satisfies Hyry’s condition
![]() $\text{H}_{G(\mathbf{I})}(G({\mathcal{F}}),\mathbf{m})$
.
$\text{H}_{G(\mathbf{I})}(G({\mathcal{F}}),\mathbf{m})$
.
Proof. Denote
![]() ${\mathcal{R}}^{\prime }({\mathcal{F}})/{\mathcal{R}}^{\prime }({\mathcal{F}})(\mathbf{e})$
by
${\mathcal{R}}^{\prime }({\mathcal{F}})/{\mathcal{R}}^{\prime }({\mathcal{F}})(\mathbf{e})$
by
![]() $G^{\prime }({\mathcal{F}})$
. Consider the short exact sequence of
$G^{\prime }({\mathcal{F}})$
. Consider the short exact sequence of
![]() ${\mathcal{R}}(\mathbf{I})$
-modules
${\mathcal{R}}(\mathbf{I})$
-modules
This induces the long exact sequence of
![]() $R$
-modules
$R$
-modules
 $$\begin{eqnarray}\displaystyle & & \displaystyle \cdots \longrightarrow [H_{{\mathcal{R}}_{++}}^{i}({\mathcal{R}}^{\prime }({\mathcal{F}}))]_{\mathbf{n}+\mathbf{e}}\longrightarrow [H_{{\mathcal{R}}_{++}}^{i}({\mathcal{R}}^{\prime }({\mathcal{F}}))]_{\mathbf{n}}\longrightarrow [H_{{\mathcal{R}}_{++}}^{i}(G^{\prime }({\mathcal{F}}))]_{\mathbf{n}}\nonumber\\ \displaystyle & & \displaystyle \quad \longrightarrow [H_{{\mathcal{R}}_{++}}^{i+1}({\mathcal{R}}^{\prime }({\mathcal{F}}))]_{\mathbf{n}+\mathbf{e}}\longrightarrow \cdots .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \cdots \longrightarrow [H_{{\mathcal{R}}_{++}}^{i}({\mathcal{R}}^{\prime }({\mathcal{F}}))]_{\mathbf{n}+\mathbf{e}}\longrightarrow [H_{{\mathcal{R}}_{++}}^{i}({\mathcal{R}}^{\prime }({\mathcal{F}}))]_{\mathbf{n}}\longrightarrow [H_{{\mathcal{R}}_{++}}^{i}(G^{\prime }({\mathcal{F}}))]_{\mathbf{n}}\nonumber\\ \displaystyle & & \displaystyle \quad \longrightarrow [H_{{\mathcal{R}}_{++}}^{i+1}({\mathcal{R}}^{\prime }({\mathcal{F}}))]_{\mathbf{n}+\mathbf{e}}\longrightarrow \cdots .\nonumber\end{eqnarray}$$
Hence, by [Reference Masuti, Sarkar and Verma11, Proposition 4.2] and the change of ring principle, we get the required result. ◻
Theorem 3.11. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring of dimension
$(R,\mathfrak{m})$
be a Noetherian local ring of dimension
![]() $d\geqslant 1$
, and let
$d\geqslant 1$
, and let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals in
$\mathfrak{m}$
-primary ideals in
![]() $R$
. Let
$R$
. Let
![]() ${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
${\mathcal{F}}=\{{\mathcal{F}}(\mathbf{n})\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
be an
![]() $\mathbf{I}$
-admissible filtration of ideals in
$\mathbf{I}$
-admissible filtration of ideals in
![]() $R$
, and let
$R$
, and let
![]() ${\mathcal{R}}({\mathcal{F}})$
satisfy Hyry’s condition
${\mathcal{R}}({\mathcal{F}})$
satisfy Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
. Let
$\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
. Let
![]() $\mathbf{q}\in \mathbb{N}^{s}$
such that
$\mathbf{q}\in \mathbb{N}^{s}$
such that
![]() $|\mathbf{q}|=d$
. Then, there exists a joint reduction
$|\mathbf{q}|=d$
. Then, there exists a joint reduction
![]() $\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
of
$\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
of
![]() ${\mathcal{F}}$
of type
${\mathcal{F}}$
of type
![]() $\mathbf{q}$
such that
$\mathbf{q}$
such that
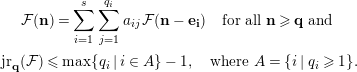 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}(\mathbf{n})=\mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})\quad \text{for all }\mathbf{n}\geqslant \mathbf{q}\text{ and } & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{jr}_{\mathbf{q}}({\mathcal{F}})\leqslant \max \{q_{i}\mid i\in A\}-1,\quad \text{where }A=\{i\mid q_{i}\geqslant 1\}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}(\mathbf{n})=\mathop{\sum }_{i=1}^{s}\mathop{\sum }_{j=1}^{q_{i}}a_{ij}{\mathcal{F}}(\mathbf{n}-\mathbf{e}_{\mathbf{i}})\quad \text{for all }\mathbf{n}\geqslant \mathbf{q}\text{ and } & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{jr}_{\mathbf{q}}({\mathcal{F}})\leqslant \max \{q_{i}\mid i\in A\}-1,\quad \text{where }A=\{i\mid q_{i}\geqslant 1\}. & \displaystyle \nonumber\end{eqnarray}$$
Proof. Since
![]() ${\mathcal{R}}({\mathcal{F}})$
satisfies Hyry’s condition
${\mathcal{R}}({\mathcal{F}})$
satisfies Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
, by Lemma 3.10,
$\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
, by Lemma 3.10,
![]() $G({\mathcal{F}})$
satisfies Hyry’s condition
$G({\mathcal{F}})$
satisfies Hyry’s condition
![]() $\text{H}_{G(\mathbf{I})}(G({\mathcal{F}}),\mathbf{0})$
. By Theorem 2.4, there exists a joint reduction
$\text{H}_{G(\mathbf{I})}(G({\mathcal{F}}),\mathbf{0})$
. By Theorem 2.4, there exists a joint reduction
![]() $\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
of
$\{a_{ij}\in I_{i}:j=1,\ldots ,q_{i};i=1,\ldots ,s\}$
of
![]() ${\mathcal{F}}$
of type
${\mathcal{F}}$
of type
![]() $\mathbf{q}$
such that
$\mathbf{q}$
such that
![]() $a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast }$
is a
$a_{11}^{\ast },\ldots ,a_{1q_{1}}^{\ast },\ldots ,a_{s1}^{\ast },\ldots ,a_{sq_{s}}^{\ast }$
is a
![]() $G({\mathcal{F}})$
-filter-regular sequence, where
$G({\mathcal{F}})$
-filter-regular sequence, where
![]() $a_{ij}^{\ast }$
is the image of
$a_{ij}^{\ast }$
is the image of
![]() $a_{ij}$
in
$a_{ij}$
in
![]() $G(\mathbf{I})_{\mathbf{e}_{\mathbf{i}}}$
for all
$G(\mathbf{I})_{\mathbf{e}_{\mathbf{i}}}$
for all
![]() $j=1,\ldots ,q_{i}$
,
$j=1,\ldots ,q_{i}$
,
![]() $i=1,\ldots ,s$
. Hence, by Theorem 3.9, for all
$i=1,\ldots ,s$
. Hence, by Theorem 3.9, for all
![]() $\mathbf{n}\geqslant \mathbf{q}$
,
$\mathbf{n}\geqslant \mathbf{q}$
,
Example 3.12. Let
![]() $R=k[|X,Y|]$
. Then,
$R=k[|X,Y|]$
. Then,
![]() $R$
is a regular local ring of dimension 2. Let
$R$
is a regular local ring of dimension 2. Let
![]() $I=(X,Y^{2})$
, and let
$I=(X,Y^{2})$
, and let
![]() $J=(X^{2},Y)$
. Then,
$J=(X^{2},Y)$
. Then,
![]() $I,J$
are complete parameter ideals in
$I,J$
are complete parameter ideals in
![]() $R$
. Consider the filtration
$R$
. Consider the filtration
![]() ${\mathcal{F}}=\{I^{r}J^{s}\}_{r,s\in \mathbb{Z}}$
. Since
${\mathcal{F}}=\{I^{r}J^{s}\}_{r,s\in \mathbb{Z}}$
. Since
![]() $I,J$
are complete ideals, by [Reference Zariski and Samuel16, Theorem 2
$I,J$
are complete ideals, by [Reference Zariski and Samuel16, Theorem 2
![]() $^{\prime }$
, Appendix 5],
$^{\prime }$
, Appendix 5],
![]() $I^{r}$
,
$I^{r}$
,
![]() $J^{s}$
and
$J^{s}$
and
![]() $I^{r}J^{s}$
are complete ideals for all
$I^{r}J^{s}$
are complete ideals for all
![]() $r,s\geqslant 1$
. By [Reference Masuti, Sarkar and Verma11, Proposition 3.2] and [Reference Masuti, Sarkar and Verma11, Proposition 3.5], for all
$r,s\geqslant 1$
. By [Reference Masuti, Sarkar and Verma11, Proposition 3.2] and [Reference Masuti, Sarkar and Verma11, Proposition 3.5], for all
![]() $r,s\in \mathbb{N}$
,
$r,s\in \mathbb{N}$
,
![]() $H_{{\mathcal{R}}_{++}}^{1}({\mathcal{R}}(I,J))_{(r,s)}=0$
. Note that
$H_{{\mathcal{R}}_{++}}^{1}({\mathcal{R}}(I,J))_{(r,s)}=0$
. Note that
![]() $(X^{3}+Y^{3},XY)$
is a minimal reduction of
$(X^{3}+Y^{3},XY)$
is a minimal reduction of
![]() $IJ$
and
$IJ$
and
Thus,
![]() $r(IJ)\leqslant 1$
and hence
$r(IJ)\leqslant 1$
and hence
![]() $e_{2}(IJ)=0$
. Therefore, using [Reference Masuti, Sarkar and Verma11, Theorem 4.3] and [Reference Masuti, Sarkar and Verma11, Lemma 2.11], we get
$e_{2}(IJ)=0$
. Therefore, using [Reference Masuti, Sarkar and Verma11, Theorem 4.3] and [Reference Masuti, Sarkar and Verma11, Lemma 2.11], we get
![]() $[H_{{\mathcal{R}}_{++}}^{2}({\mathcal{R}}(I,J))]_{(r,s)}=0$
for all
$[H_{{\mathcal{R}}_{++}}^{2}({\mathcal{R}}(I,J))]_{(r,s)}=0$
for all
![]() $r,s\in \mathbb{N}$
. Hence,
$r,s\in \mathbb{N}$
. Hence,
![]() ${\mathcal{R}}({\mathcal{F}})$
satisfies Hyry’s condition
${\mathcal{R}}({\mathcal{F}})$
satisfies Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
.
$\text{H}_{{\mathcal{R}}(\mathbf{I})}({\mathcal{R}}({\mathcal{F}}),\mathbf{0})$
.
Note that
![]() ${\mathcal{A}}_{\mathbf{e}}=\{X,Y\}$
is a joint reduction of
${\mathcal{A}}_{\mathbf{e}}=\{X,Y\}$
is a joint reduction of
![]() $(I,J)$
of type
$(I,J)$
of type
![]() $\mathbf{e}$
and
$\mathbf{e}$
and
Thus,
![]() $\text{jr}_{\mathbf{e}}({\mathcal{F}})=\text{jr}_{{\mathcal{A}}_{\mathbf{e}}}({\mathcal{F}})=0$
.
$\text{jr}_{\mathbf{e}}({\mathcal{F}})=\text{jr}_{{\mathcal{A}}_{\mathbf{e}}}({\mathcal{F}})=0$
.
Theorem 3.13. Let
![]() $(R,\mathfrak{m})$
be an analytically unramified Noetherian local ring of dimension
$(R,\mathfrak{m})$
be an analytically unramified Noetherian local ring of dimension
![]() $d\geqslant 2$
, and let
$d\geqslant 2$
, and let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary ideals in
$\mathfrak{m}$
-primary ideals in
![]() $R$
. Let
$R$
. Let
![]() $\overline{{\mathcal{R}}}(\mathbf{I})=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}\overline{\mathbf{I}^{\mathbf{n}}}$
satisfy Hyry’s condition
$\overline{{\mathcal{R}}}(\mathbf{I})=\bigoplus _{\mathbf{n}\in \mathbb{N}^{s}}\overline{\mathbf{I}^{\mathbf{n}}}$
satisfy Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}(\overline{{\mathcal{R}}}(\mathbf{I}),\mathbf{0})$
. Suppose that
$\text{H}_{{\mathcal{R}}(\mathbf{I})}(\overline{{\mathcal{R}}}(\mathbf{I}),\mathbf{0})$
. Suppose that
![]() $\mathbf{I}^{\mathbf{n}}$
is complete for all
$\mathbf{I}^{\mathbf{n}}$
is complete for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
such that
$\mathbf{n}\in \mathbb{N}^{s}$
such that
![]() $1\leqslant |\mathbf{n}|\leqslant d-1$
. Then,
$1\leqslant |\mathbf{n}|\leqslant d-1$
. Then,
![]() $\mathbf{I}^{\mathbf{n}}$
is complete for all
$\mathbf{I}^{\mathbf{n}}$
is complete for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
with
$\mathbf{n}\in \mathbb{N}^{s}$
with
![]() $|\mathbf{n}|\geqslant 1$
.
$|\mathbf{n}|\geqslant 1$
.
Proof. We use induction on
![]() $|\mathbf{n}|$
. By the given hypothesis, the result is true up to
$|\mathbf{n}|$
. By the given hypothesis, the result is true up to
![]() $1\leqslant |\mathbf{n}|\leqslant d-1$
. Suppose that
$1\leqslant |\mathbf{n}|\leqslant d-1$
. Suppose that
![]() $\mathbf{n}\in \mathbb{N}^{s}$
with
$\mathbf{n}\in \mathbb{N}^{s}$
with
![]() $|\mathbf{n}|\geqslant d$
, and the result is true for all
$|\mathbf{n}|\geqslant d$
, and the result is true for all
![]() $\mathbf{k}\in \mathbb{N}^{s}$
such that
$\mathbf{k}\in \mathbb{N}^{s}$
such that
![]() $1\leqslant |\mathbf{k}|<|\mathbf{n}|$
. Let
$1\leqslant |\mathbf{k}|<|\mathbf{n}|$
. Let
![]() $\mathbf{m}=(m_{1},\ldots ,m_{s})\in \mathbb{N}^{s}$
such that
$\mathbf{m}=(m_{1},\ldots ,m_{s})\in \mathbb{N}^{s}$
such that
![]() $\mathbf{m}\leqslant \mathbf{n}$
and
$\mathbf{m}\leqslant \mathbf{n}$
and
![]() $|\mathbf{m}|=d$
. Consider the filtration
$|\mathbf{m}|=d$
. Consider the filtration
![]() ${\mathcal{F}}=\{\overline{\mathbf{I}^{\mathbf{n}}}\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
. By [Reference Rees12],
${\mathcal{F}}=\{\overline{\mathbf{I}^{\mathbf{n}}}\}_{\mathbf{n}\in \mathbb{Z}^{s}}$
. By [Reference Rees12],
![]() ${\mathcal{F}}$
is an
${\mathcal{F}}$
is an
![]() $\mathbf{I}$
-admissible filtration. Then, by Theorems 2.4 and 3.9, there exists a joint reduction
$\mathbf{I}$
-admissible filtration. Then, by Theorems 2.4 and 3.9, there exists a joint reduction
![]() $\{a_{ij}\in I_{i}:j=1,\ldots ,m_{i};i=1,\ldots ,s\}$
of
$\{a_{ij}\in I_{i}:j=1,\ldots ,m_{i};i=1,\ldots ,s\}$
of
![]() ${\mathcal{F}}$
of type
${\mathcal{F}}$
of type
![]() $\mathbf{m}$
such that
$\mathbf{m}$
such that
Thus,
![]() $\overline{\mathbf{I}^{\mathbf{n}}}=\sum _{i=1}^{s}\sum _{j=1}^{m_{i}}a_{ij}\overline{\mathbf{I}^{\mathbf{n}-\mathbf{e}_{\mathbf{i}}}}$
. By induction hypothesis,
$\overline{\mathbf{I}^{\mathbf{n}}}=\sum _{i=1}^{s}\sum _{j=1}^{m_{i}}a_{ij}\overline{\mathbf{I}^{\mathbf{n}-\mathbf{e}_{\mathbf{i}}}}$
. By induction hypothesis,
![]() $\mathbf{I}^{\mathbf{n}-\mathbf{e}_{\mathbf{i}}}$
is complete for all
$\mathbf{I}^{\mathbf{n}-\mathbf{e}_{\mathbf{i}}}$
is complete for all
![]() $i\in A:=\{i|n_{i}\geqslant 1\}$
. Hence,
$i\in A:=\{i|n_{i}\geqslant 1\}$
. Hence,
As a consequence of the above theorem, we obtain a generalization of a theorem of Reid, Roberts and Vitulli [Reference Reid, Roberts and Vitulli13, Proposition 3.1] about complete monomial ideals.
Theorem 3.14. Let
![]() $R=k[X_{1},\ldots ,X_{d}]$
be a polynomial ring over a field
$R=k[X_{1},\ldots ,X_{d}]$
be a polynomial ring over a field
![]() $k$
, let
$k$
, let
![]() $d\geqslant 1$
, and let
$d\geqslant 1$
, and let
![]() $\mathfrak{m}$
be the maximal homogeneous ideal of
$\mathfrak{m}$
be the maximal homogeneous ideal of
![]() $R$
. Let
$R$
. Let
![]() $I_{1},\ldots ,I_{s}$
be
$I_{1},\ldots ,I_{s}$
be
![]() $\mathfrak{m}$
-primary monomial ideals of
$\mathfrak{m}$
-primary monomial ideals of
![]() $R$
. Suppose that
$R$
. Suppose that
![]() $\mathbf{I}^{\mathbf{n}}$
is complete for all
$\mathbf{I}^{\mathbf{n}}$
is complete for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
such that
$\mathbf{n}\in \mathbb{N}^{s}$
such that
![]() $1\leqslant |\mathbf{n}|\leqslant d-1$
. Then,
$1\leqslant |\mathbf{n}|\leqslant d-1$
. Then,
![]() $\mathbf{I}^{\mathbf{n}}$
is complete for all
$\mathbf{I}^{\mathbf{n}}$
is complete for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
with
$\mathbf{n}\in \mathbb{N}^{s}$
with
![]() $|\mathbf{n}|\geqslant 1$
.
$|\mathbf{n}|\geqslant 1$
.
Proof. If
![]() $d=1$
, then
$d=1$
, then
![]() $R$
is a principal ideal domain (PID), and hence normal. Therefore, every ideal is complete since principal ideals in normal domains are complete. Let
$R$
is a principal ideal domain (PID), and hence normal. Therefore, every ideal is complete since principal ideals in normal domains are complete. Let
![]() $d\geqslant 2$
. Since
$d\geqslant 2$
. Since
![]() $I_{1},\ldots ,I_{s}$
are monomial ideals,
$I_{1},\ldots ,I_{s}$
are monomial ideals,
![]() $\overline{{\mathcal{R}}}(\mathbf{I})$
is Cohen–Macaulay by [Reference Bruns and Herzog2, Theorem 6.3.5]. Let
$\overline{{\mathcal{R}}}(\mathbf{I})$
is Cohen–Macaulay by [Reference Bruns and Herzog2, Theorem 6.3.5]. Let
![]() $W=R\setminus \mathfrak{m}$
. Then,
$W=R\setminus \mathfrak{m}$
. Then,
![]() $S=W^{-1}\overline{{\mathcal{R}}}(\mathbf{I})$
is Cohen–Macaulay. Since for any ideal
$S=W^{-1}\overline{{\mathcal{R}}}(\mathbf{I})$
is Cohen–Macaulay. Since for any ideal
![]() $I$
,
$I$
,
![]() $W^{-1}\overline{I}=\overline{W^{-1}I}$
, we have
$W^{-1}\overline{I}=\overline{W^{-1}I}$
, we have
Therefore,
![]() $S$
satisfies Hyry’s condition
$S$
satisfies Hyry’s condition
![]() $\text{H}_{Q}(S,\mathbf{0})$
, where
$\text{H}_{Q}(S,\mathbf{0})$
, where
![]() $Q=W^{-1}{\mathcal{R}}(\mathbf{I})$
. Replace
$Q=W^{-1}{\mathcal{R}}(\mathbf{I})$
. Replace
![]() $R$
by
$R$
by
![]() $W^{-1}R$
. Therefore, by Theorem 3.13,
$W^{-1}R$
. Therefore, by Theorem 3.13,
![]() $W^{-1}(\mathbf{I}^{\mathbf{n}})$
is complete for all
$W^{-1}(\mathbf{I}^{\mathbf{n}})$
is complete for all
![]() $\mathbf{n}\in \mathbb{N}^{s}$
such that
$\mathbf{n}\in \mathbb{N}^{s}$
such that
![]() $|\mathbf{n}|\geqslant 1$
. Since
$|\mathbf{n}|\geqslant 1$
. Since
![]() $\mathfrak{m}$
is the maximal homogeneous ideal of
$\mathfrak{m}$
is the maximal homogeneous ideal of
![]() $R$
and
$R$
and
![]() $W^{-1}(\overline{\mathbf{I}^{\mathbf{n}}}/\mathbf{I}^{\mathbf{n}})=0$
, we get the required result.◻
$W^{-1}(\overline{\mathbf{I}^{\mathbf{n}}}/\mathbf{I}^{\mathbf{n}})=0$
, we get the required result.◻
We end the paper with three examples illustrating some of the results proved above.
Example 3.15. Let
![]() $S=\mathbb{Q}[[X,Y,Z]]$
, and let
$S=\mathbb{Q}[[X,Y,Z]]$
, and let
![]() $f=X^{2}+Y^{2}+Z^{2}$
. Then,
$f=X^{2}+Y^{2}+Z^{2}$
. Then,
![]() $R=S/(f)$
is an analytically unramified Cohen–Macaulay reduced local ring of dimension
$R=S/(f)$
is an analytically unramified Cohen–Macaulay reduced local ring of dimension
![]() $2$
. Set
$2$
. Set
![]() $\mathfrak{m}=(X,Y,Z)/(f)$
. Since
$\mathfrak{m}=(X,Y,Z)/(f)$
. Since
![]() $G_{\mathfrak{m}}(R)\simeq \mathbb{Q}[X,Y,Z]/(f)$
is reduced,
$G_{\mathfrak{m}}(R)\simeq \mathbb{Q}[X,Y,Z]/(f)$
is reduced,
![]() $\mathfrak{m}^{n}$
is complete for all
$\mathfrak{m}^{n}$
is complete for all
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
Consider the
![]() $\mathfrak{m}$
-admissible filtration
$\mathfrak{m}$
-admissible filtration
![]() ${\mathcal{F}}=\{\overline{\mathfrak{m}^{n}}\}_{n\in \mathbb{Z}}$
. The Hilbert polynomial of the filtration
${\mathcal{F}}=\{\overline{\mathfrak{m}^{n}}\}_{n\in \mathbb{Z}}$
. The Hilbert polynomial of the filtration
![]() ${\mathcal{F}}$
is
${\mathcal{F}}$
is
![]() $P_{{\mathcal{F}}}(n)=2\binom{n+1}{2}-n$
. Set
$P_{{\mathcal{F}}}(n)=2\binom{n+1}{2}-n$
. Set
![]() ${\mathcal{R}}={\mathcal{R}}(\mathfrak{m})$
. Since
${\mathcal{R}}={\mathcal{R}}(\mathfrak{m})$
. Since
![]() $R$
is Cohen–Macaulay,
$R$
is Cohen–Macaulay,
![]() $H_{{\mathcal{R}}_{++}}^{0}({\mathcal{R}}(\mathfrak{m}))=0$
. By [Reference Blancafort1, Theorem 3.5],
$H_{{\mathcal{R}}_{++}}^{0}({\mathcal{R}}(\mathfrak{m}))=0$
. By [Reference Blancafort1, Theorem 3.5],
![]() $[H_{{\mathcal{R}}_{++}}^{1}({\mathcal{R}}(\mathfrak{m}))]_{n}=\widetilde{\overline{\mathfrak{m}^{n}}}/\overline{\mathfrak{m}^{n}}$
for all
$[H_{{\mathcal{R}}_{++}}^{1}({\mathcal{R}}(\mathfrak{m}))]_{n}=\widetilde{\overline{\mathfrak{m}^{n}}}/\overline{\mathfrak{m}^{n}}$
for all
![]() $n\geqslant 0$
, where
$n\geqslant 0$
, where
![]() $\{\widetilde{\overline{\mathfrak{m}^{n}}}\}_{n\in \mathbb{Z}}$
is the Ratliff–Rush closure filtration of
$\{\widetilde{\overline{\mathfrak{m}^{n}}}\}_{n\in \mathbb{Z}}$
is the Ratliff–Rush closure filtration of
![]() ${\mathcal{F}}$
. Therefore, by [Reference Masuti, Sarkar and Verma11, Proposition 3.2],
${\mathcal{F}}$
. Therefore, by [Reference Masuti, Sarkar and Verma11, Proposition 3.2],
![]() $[H_{{\mathcal{R}}_{++}}^{1}({\mathcal{R}}(\mathfrak{m}))]_{n}=0$
for all
$[H_{{\mathcal{R}}_{++}}^{1}({\mathcal{R}}(\mathfrak{m}))]_{n}=0$
for all
![]() $n\geqslant 0$
. By [Reference Blancafort1, Theorem 4.1], we get
$n\geqslant 0$
. By [Reference Blancafort1, Theorem 4.1], we get
![]() $[H_{{\mathcal{R}}_{++}}^{2}({\mathcal{R}}(\mathfrak{m}))]_{0}=0$
. Hence, by [Reference Blancafort1, Lemma 4.7],
$[H_{{\mathcal{R}}_{++}}^{2}({\mathcal{R}}(\mathfrak{m}))]_{0}=0$
. Hence, by [Reference Blancafort1, Lemma 4.7],
![]() $[H_{{\mathcal{R}}_{++}}^{2}({\mathcal{R}}(\mathfrak{m}))]_{n}=0$
for all
$[H_{{\mathcal{R}}_{++}}^{2}({\mathcal{R}}(\mathfrak{m}))]_{n}=0$
for all
![]() $n\geqslant 0$
. Hence,
$n\geqslant 0$
. Hence,
![]() ${\mathcal{R}}(\mathfrak{m})$
satisfies the condition
${\mathcal{R}}(\mathfrak{m})$
satisfies the condition
![]() $\text{H}_{{\mathcal{R}}(\mathfrak{m})}({\mathcal{R}}(\mathfrak{m}),0)$
.
$\text{H}_{{\mathcal{R}}(\mathfrak{m})}({\mathcal{R}}(\mathfrak{m}),0)$
.
The following examples show that Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathbf{I})}(\overline{{\mathcal{R}}}(\mathbf{I}),\mathbf{0})$
is sufficient but not necessary in Theorem 3.13.
$\text{H}_{{\mathcal{R}}(\mathbf{I})}(\overline{{\mathcal{R}}}(\mathbf{I}),\mathbf{0})$
is sufficient but not necessary in Theorem 3.13.
Example 3.16. Let
![]() $S=\mathbb{Q}[[X,Y,Z]]$
, and let
$S=\mathbb{Q}[[X,Y,Z]]$
, and let
![]() $g=X^{3}+Y^{3}+Z^{3}$
. Then,
$g=X^{3}+Y^{3}+Z^{3}$
. Then,
![]() $R=S/(g)$
is an analytically unramified Cohen–Macaulay reduced local ring of dimension
$R=S/(g)$
is an analytically unramified Cohen–Macaulay reduced local ring of dimension
![]() $2$
. Set
$2$
. Set
![]() $\mathfrak{m}=(X,Y,Z)/(g)$
. Since
$\mathfrak{m}=(X,Y,Z)/(g)$
. Since
![]() $G_{\mathfrak{m}}(R)\simeq \mathbb{Q}[X,Y,Z]/(g)$
is reduced,
$G_{\mathfrak{m}}(R)\simeq \mathbb{Q}[X,Y,Z]/(g)$
is reduced,
![]() $\mathfrak{m}^{n}$
is complete for all
$\mathfrak{m}^{n}$
is complete for all
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
Consider the
![]() $\mathfrak{m}$
-admissible filtration
$\mathfrak{m}$
-admissible filtration
![]() ${\mathcal{F}}=\{\overline{\mathfrak{m}^{n}}\}_{n\in \mathbb{Z}}$
. The Hilbert polynomial of the filtration
${\mathcal{F}}=\{\overline{\mathfrak{m}^{n}}\}_{n\in \mathbb{Z}}$
. The Hilbert polynomial of the filtration
![]() ${\mathcal{F}}$
is
${\mathcal{F}}$
is
![]() $P_{{\mathcal{F}}}(n)=3\binom{n+1}{2}-3n+1$
. Set
$P_{{\mathcal{F}}}(n)=3\binom{n+1}{2}-3n+1$
. Set
![]() ${\mathcal{R}}={\mathcal{R}}(\mathfrak{m})$
. Since
${\mathcal{R}}={\mathcal{R}}(\mathfrak{m})$
. Since
![]() $R$
is Cohen–Macaulay,
$R$
is Cohen–Macaulay,
![]() $H_{{\mathcal{R}}_{++}}^{0}({\mathcal{R}}(\mathfrak{m}))=0$
. By [Reference Blancafort1, Theorem 3.5],
$H_{{\mathcal{R}}_{++}}^{0}({\mathcal{R}}(\mathfrak{m}))=0$
. By [Reference Blancafort1, Theorem 3.5],
![]() $[H_{{\mathcal{R}}_{++}}^{1}({\mathcal{R}}(\mathfrak{m}))]_{n}=\widetilde{\overline{\mathfrak{m}^{n}}}/\overline{\mathfrak{m}^{n}}$
for all
$[H_{{\mathcal{R}}_{++}}^{1}({\mathcal{R}}(\mathfrak{m}))]_{n}=\widetilde{\overline{\mathfrak{m}^{n}}}/\overline{\mathfrak{m}^{n}}$
for all
![]() $n\geqslant 0$
. (Here,
$n\geqslant 0$
. (Here,
![]() $\{\widetilde{\overline{\mathfrak{m}^{n}}}\}_{n\in \mathbb{Z}}$
is the Ratliff–Rush closure filtration of
$\{\widetilde{\overline{\mathfrak{m}^{n}}}\}_{n\in \mathbb{Z}}$
is the Ratliff–Rush closure filtration of
![]() ${\mathcal{F}}$
.) Therefore,
${\mathcal{F}}$
.) Therefore,
![]() $[H_{{\mathcal{R}}_{++}}^{1}({\mathcal{R}}(\mathfrak{m}))]_{n}=0$
for all
$[H_{{\mathcal{R}}_{++}}^{1}({\mathcal{R}}(\mathfrak{m}))]_{n}=0$
for all
![]() $n\geqslant 0$
. By [Reference Blancafort1, Theorem 4.1], we get
$n\geqslant 0$
. By [Reference Blancafort1, Theorem 4.1], we get
![]() $\unicode[STIX]{x1D706}(H_{{\mathcal{R}}_{++}}^{2}({\mathcal{R}}(\mathfrak{m})))_{0}=1$
. Hence,
$\unicode[STIX]{x1D706}(H_{{\mathcal{R}}_{++}}^{2}({\mathcal{R}}(\mathfrak{m})))_{0}=1$
. Hence,
![]() ${\mathcal{R}}(\mathfrak{m})$
does not satisfy Hyry’s condition
${\mathcal{R}}(\mathfrak{m})$
does not satisfy Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(\mathfrak{m})}({\mathcal{R}}(\mathfrak{m}),0)$
.
$\text{H}_{{\mathcal{R}}(\mathfrak{m})}({\mathcal{R}}(\mathfrak{m}),0)$
.
Example 3.17. Let
![]() $R=k[x,y,z]$
, where
$R=k[x,y,z]$
, where
![]() $k$
is a field of characteristic not equal to
$k$
is a field of characteristic not equal to
![]() $3$
, and let
$3$
, and let
![]() $I=(x^{4},x(y^{3}+z^{3}),y(y^{3}+z^{3}),z(y^{3}+z^{3}))+(x,y,z)^{5}$
. In [Reference Huckaba and Huneke4, Theorem 3.12], Huckaba and Huneke showed that
$I=(x^{4},x(y^{3}+z^{3}),y(y^{3}+z^{3}),z(y^{3}+z^{3}))+(x,y,z)^{5}$
. In [Reference Huckaba and Huneke4, Theorem 3.12], Huckaba and Huneke showed that
![]() $\text{ht}(I)=3$
,
$\text{ht}(I)=3$
,
![]() $I$
is normal ideal; that is,
$I$
is normal ideal; that is,
![]() $\overline{I^{n}}=I^{n}$
for all
$\overline{I^{n}}=I^{n}$
for all
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $H^{2}(X,\mathscr{O}_{X})\neq 0$
, where
$H^{2}(X,\mathscr{O}_{X})\neq 0$
, where
![]() $X=\text{Proj}\,{\mathcal{R}}(I)$
. Hence,
$X=\text{Proj}\,{\mathcal{R}}(I)$
. Hence,
![]() $H_{{\mathcal{R}}_{++}}^{3}({\mathcal{R}}(I))_{0}\neq 0$
. Thus,
$H_{{\mathcal{R}}_{++}}^{3}({\mathcal{R}}(I))_{0}\neq 0$
. Thus,
![]() ${\mathcal{R}}(I)$
does not satisfy Hyry’s condition
${\mathcal{R}}(I)$
does not satisfy Hyry’s condition
![]() $\text{H}_{{\mathcal{R}}(I)}({\mathcal{R}}(I),0)$
.
$\text{H}_{{\mathcal{R}}(I)}({\mathcal{R}}(I),0)$
.


