Article contents
Liouvillian solutions of second order differential equation without Fuchsian singularities
Published online by Cambridge University Press: 22 January 2016
Extract
Consider a homogeneous linear differential equation of the second order whose coefficients are rational functions of the independent variable x over the field C of complex numbers. We assume that the coefficient of the first order derivative vanishes:
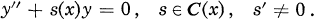
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1986
References
- 2
- Cited by


