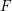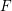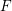1 Introduction
Let
![]() $R$
denote a polynomial ring over a field of characteristic
$R$
denote a polynomial ring over a field of characteristic
![]() $p>0$
with homogeneous maximal ideal
$p>0$
with homogeneous maximal ideal
![]() $\mathfrak{m}$
. Given an ideal
$\mathfrak{m}$
. Given an ideal
![]() $\mathfrak{a}$
of
$\mathfrak{a}$
of
![]() $R$
contained in
$R$
contained in
![]() $\mathfrak{m}$
, the
$\mathfrak{m}$
, the
![]() $F$
-pure threshold of
$F$
-pure threshold of
![]() $\mathfrak{a}$
(at the origin) is a numerical invariant measuring the singularities of
$\mathfrak{a}$
(at the origin) is a numerical invariant measuring the singularities of
![]() $\mathfrak{a}$
near the origin, and is closely related to the theory of
$\mathfrak{a}$
near the origin, and is closely related to the theory of
![]() $F$
-purity and tight closure (see [Reference Hochster and RobertsHR76, Reference Hochster and HunekeHH90, Reference Hara and YoshidaHY03]).
$F$
-purity and tight closure (see [Reference Hochster and RobertsHR76, Reference Hochster and HunekeHH90, Reference Hara and YoshidaHY03]).
In this article, we are particularly interested in the connection between the
![]() $F$
-pure threshold of a polynomial
$F$
-pure threshold of a polynomial
![]() $f\in \mathfrak{m}$
, and the
$f\in \mathfrak{m}$
, and the
![]() $F$
-pure threshold of
$F$
-pure threshold of
![]() $\mathfrak{a}_{f}$
, the monomial ideal generated by the terms of
$\mathfrak{a}_{f}$
, the monomial ideal generated by the terms of
![]() $f$
. The basic relationship between these two invariants, which essentially follows from the containment
$f$
. The basic relationship between these two invariants, which essentially follows from the containment
![]() $f\in \mathfrak{a}_{f}$
, is the following upper bound for
$f\in \mathfrak{a}_{f}$
, is the following upper bound for
![]() $\mathbf{fpt}(f)$
:
$\mathbf{fpt}(f)$
:
This inequality may be strict: if
![]() $f=x^{p}+y^{p}$
, then
$f=x^{p}+y^{p}$
, then
![]() $\mathbf{fpt}(f)=\frac{1}{p}$
, while
$\mathbf{fpt}(f)=\frac{1}{p}$
, while
![]() $\mathbf{fpt}(\mathfrak{a}_{f})=\frac{2}{p}$
.
$\mathbf{fpt}(\mathfrak{a}_{f})=\frac{2}{p}$
.
In the first part of this article, we aim to understand when equality holds in (1.1). In Definition 17, we associate to a polynomial
![]() $f$
(over a field of arbitrary characteristic) a rational polytope
$f$
(over a field of arbitrary characteristic) a rational polytope
![]() $\mathbf{P}$
, called the splitting polytope of
$\mathbf{P}$
, called the splitting polytope of
![]() $f$
. The splitting polytope
$f$
. The splitting polytope
![]() $\mathbf{P}$
is closely related to the familiar Newton polyhedron
$\mathbf{P}$
is closely related to the familiar Newton polyhedron
![]() $\mathbf{N}$
associated to
$\mathbf{N}$
associated to
![]() $\mathfrak{a}_{f}$
. However,
$\mathfrak{a}_{f}$
. However,
![]() $\mathbf{P}$
and
$\mathbf{P}$
and
![]() $\mathbf{N}$
differ in the following crucial way: the Newton polyhedron depends only on the ideal
$\mathbf{N}$
differ in the following crucial way: the Newton polyhedron depends only on the ideal
![]() $\mathfrak{a}_{f}$
generated by the terms of
$\mathfrak{a}_{f}$
generated by the terms of
![]() $f$
, while the splitting polytope depends strongly on the terms themselves. For example,
$f$
, while the splitting polytope depends strongly on the terms themselves. For example,
![]() $\mathbf{P}$
is always contained in the
$\mathbf{P}$
is always contained in the
![]() $n$
-fold product of the unit interval (here,
$n$
-fold product of the unit interval (here,
![]() $n$
denotes the number of terms of
$n$
denotes the number of terms of
![]() $f$
), while
$f$
), while
![]() $\mathbf{N}$
is always a full-dimensional polyhedron in
$\mathbf{N}$
is always a full-dimensional polyhedron in
![]() $\mathbb{R}^{m}$
(here,
$\mathbb{R}^{m}$
(here,
![]() $m$
denotes the number of variables in the ambient polynomial ring). In Section 4, we identify conditions on the Newton polyhedron
$m$
denotes the number of variables in the ambient polynomial ring). In Section 4, we identify conditions on the Newton polyhedron
![]() $\mathbf{N}$
, the splitting polytope
$\mathbf{N}$
, the splitting polytope
![]() $\mathbf{P}$
, and the characteristic
$\mathbf{P}$
, and the characteristic
![]() $p$
under which equality holds in (1.1). As these conditions are rather technical, we omit them here, and instead refer the reader to Theorem 42 and Proposition 40.
$p$
under which equality holds in (1.1). As these conditions are rather technical, we omit them here, and instead refer the reader to Theorem 42 and Proposition 40.
1.1 Log canonicity versus
 $F$
-purity
$F$
-purity
We now switch gears and consider an invariant of singularities defined over
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $S$
be a polynomial ring over
$S$
be a polynomial ring over
![]() $\mathbb{C}$
, and let
$\mathbb{C}$
, and let
![]() $\mathfrak{a}$
be an ideal contained in the homogeneous maximal ideal of
$\mathfrak{a}$
be an ideal contained in the homogeneous maximal ideal of
![]() $S$
. The log canonical threshold of
$S$
. The log canonical threshold of
![]() $\mathfrak{a}$
(at the origin), denoted
$\mathfrak{a}$
(at the origin), denoted
![]() $\mathbf{lct}(\mathfrak{a})$
, is a numerical invariant measuring the singularities of
$\mathbf{lct}(\mathfrak{a})$
, is a numerical invariant measuring the singularities of
![]() $\mathfrak{a}$
at the origin, and plays an important role in higher-dimensional birational geometry (see [Reference Blickle and LazarsfeldBL04, Reference LazarsfeldLaz04]). Remarkably,
$\mathfrak{a}$
at the origin, and plays an important role in higher-dimensional birational geometry (see [Reference Blickle and LazarsfeldBL04, Reference LazarsfeldLaz04]). Remarkably,
![]() $F$
-pure thresholds can be thought of as the positive characteristic analog of log canonical thresholds (see [Reference SmithSmi00, Reference Hara and WatanabeHW02, Reference Hara and YoshidaHY03, Reference TakagiTak04]). We now sketch the relationship between these two invariants. If
$F$
-pure thresholds can be thought of as the positive characteristic analog of log canonical thresholds (see [Reference SmithSmi00, Reference Hara and WatanabeHW02, Reference Hara and YoshidaHY03, Reference TakagiTak04]). We now sketch the relationship between these two invariants. If
![]() $f$
has rational coefficients, one may reduce them modulo
$f$
has rational coefficients, one may reduce them modulo
![]() $p\gg 0$
to obtain polynomials
$p\gg 0$
to obtain polynomials
![]() $f_{p}$
over the finite fields
$f_{p}$
over the finite fields
![]() $\mathbb{F}_{p}$
. If
$\mathbb{F}_{p}$
. If
![]() $f$
has complex (but not necessarily rational) coefficients, a generalization of this method, called the process of reduction to positive characteristic, allows one to produce a family of positive characteristic models
$f$
has complex (but not necessarily rational) coefficients, a generalization of this method, called the process of reduction to positive characteristic, allows one to produce a family of positive characteristic models
![]() $f_{p}$
over finite fields of characteristic
$f_{p}$
over finite fields of characteristic
![]() $p$
. Using the results of [Reference Hara and YoshidaHY03], it is observed in [Reference Mustaţǎ, Takagi and WatanabeMTW05] that
$p$
. Using the results of [Reference Hara and YoshidaHY03], it is observed in [Reference Mustaţǎ, Takagi and WatanabeMTW05] that
We say that log canonicity equals dense (respectively, open)
![]() $F$
-pure type for
$F$
-pure type for
![]() $f$
whenever
$f$
whenever
![]() $\mathbf{fpt}(f_{p})=\mathbf{lct}(f)$
for infinitely many
$\mathbf{fpt}(f_{p})=\mathbf{lct}(f)$
for infinitely many
![]() $p$
(respectively, for all
$p$
(respectively, for all
![]() $p\gg 0$
) (see Remark 55 for a justification of this terminology). It is conjectured that log canonicity always equals dense
$p\gg 0$
) (see Remark 55 for a justification of this terminology). It is conjectured that log canonicity always equals dense
![]() $F$
-pure type, and verification of this correspondence is a long-standing open problem (see [Reference FedderFed83, Reference SmithSmi97, Reference Ein and Mustaţă EM06]). We now summarize the related results in this article.
$F$
-pure type, and verification of this correspondence is a long-standing open problem (see [Reference FedderFed83, Reference SmithSmi97, Reference Ein and Mustaţă EM06]). We now summarize the related results in this article.
Theorem A. (Cf. Theorem 56)
Let
![]() $f$
denote a polynomial over
$f$
denote a polynomial over
![]() $\mathbb{C}$
vanishing at the origin. If the supporting monomials of
$\mathbb{C}$
vanishing at the origin. If the supporting monomials of
![]() $f$
satisfy a certain nondegeneracy condition, then there exists a simple characterization of the set of all primes
$f$
satisfy a certain nondegeneracy condition, then there exists a simple characterization of the set of all primes
![]() $p$
for which
$p$
for which
![]() $\mathbf{fpt}(f_{p})=\mathbf{lct}(f)$
. Moreover, this characterization shows that log canonicity equals dense
$\mathbf{fpt}(f_{p})=\mathbf{lct}(f)$
. Moreover, this characterization shows that log canonicity equals dense
![]() $F$
-pure type for
$F$
-pure type for
![]() $f$
.
$f$
.
For the precise statement (including the description of the nondegeneracy condition, which may be stated in terms of the associated splitting polytope
![]() $\mathbf{P}$
and Newton polyhedra
$\mathbf{P}$
and Newton polyhedra
![]() $\mathbf{N}$
), we refer the reader to Theorem 56. We note that the techniques used in proving Theorem 56 are related to those used by Shibuta and Takagi in their calculation of log canonical thresholds of binomial ideals appearing in [Reference Shibuta and TakagiST09].
$\mathbf{N}$
), we refer the reader to Theorem 56. We note that the techniques used in proving Theorem 56 are related to those used by Shibuta and Takagi in their calculation of log canonical thresholds of binomial ideals appearing in [Reference Shibuta and TakagiST09].
Theorem B. (Cf. Theorem 58)
Let
![]() $f$
be a polynomial over
$f$
be a polynomial over
![]() $\mathbb{C}$
vanishing at the origin. If the coefficients appearing in the terms of
$\mathbb{C}$
vanishing at the origin. If the coefficients appearing in the terms of
![]() $f$
form an algebraically independent sequence over
$f$
form an algebraically independent sequence over
![]() $\mathbb{Q}$
, then log canonicity equals dense
$\mathbb{Q}$
, then log canonicity equals dense
![]() $F$
-pure type for
$F$
-pure type for
![]() $f$
.
$f$
.
These theorems differ in an important way: the first requires some nondegeneracy of the supporting monomials of
![]() $f$
, but assumes nothing about the coefficients of
$f$
, but assumes nothing about the coefficients of
![]() $f$
, while the second requires some generality of the coefficients of
$f$
, while the second requires some generality of the coefficients of
![]() $f$
, but assumes nothing about the supporting monomials. Moreover, under certain conditions, the first theorem characterizes the set of primes for which the
$f$
, but assumes nothing about the supporting monomials. Moreover, under certain conditions, the first theorem characterizes the set of primes for which the
![]() $F$
-pure and log canonical thresholds agree, while the second provides no such characterization.
$F$
-pure and log canonical thresholds agree, while the second provides no such characterization.
We now outline our method for establishing these results. Let
![]() $f$
denote a polynomial over
$f$
denote a polynomial over
![]() $\mathbb{C}$
, and let
$\mathbb{C}$
, and let
![]() $\mathfrak{a}_{f}$
denote its term ideal. An important component of our argument relies on the fact that the characteristic zero analog of (1.1) holds, that is, on the fact that
$\mathfrak{a}_{f}$
denote its term ideal. An important component of our argument relies on the fact that the characteristic zero analog of (1.1) holds, that is, on the fact that
Let
![]() $f_{p}$
denote the reduction of
$f_{p}$
denote the reduction of
![]() $f$
to characteristic
$f$
to characteristic
![]() $p\gg 0$
. For such
$p\gg 0$
. For such
![]() $p$
, the monomials appearing in
$p$
, the monomials appearing in
![]() $f$
and
$f$
and
![]() $f_{p}$
agree, so that
$f_{p}$
agree, so that
![]() $\mathfrak{a}_{f}$
and
$\mathfrak{a}_{f}$
and
![]() $\mathfrak{a}_{f_{p}}$
(the term ideals of
$\mathfrak{a}_{f_{p}}$
(the term ideals of
![]() $f$
and
$f$
and
![]() $f_{p}$
) are generated by the same monomials. Moreover, it follows from [Reference Hara and YoshidaHY03] that
$f_{p}$
) are generated by the same monomials. Moreover, it follows from [Reference Hara and YoshidaHY03] that
![]() $\mathbf{fpt}(\mathfrak{a}_{f_{p}})=\mathbf{lct}(\mathfrak{a}_{f})\text{ for }p\gg 0$
. Using results referenced earlier in this introduction (i.e., Theorem 42 and Proposition 40), we are able to show that
$\mathbf{fpt}(\mathfrak{a}_{f_{p}})=\mathbf{lct}(\mathfrak{a}_{f})\text{ for }p\gg 0$
. Using results referenced earlier in this introduction (i.e., Theorem 42 and Proposition 40), we are able to show that
![]() $\mathbf{fpt}(f_{p})=\min \{1,\mathbf{fpt}(\mathfrak{a}_{f_{p}})\}$
for infinitely (or all but finitely) many
$\mathbf{fpt}(f_{p})=\min \{1,\mathbf{fpt}(\mathfrak{a}_{f_{p}})\}$
for infinitely (or all but finitely) many
![]() $p$
, and an application of the relations in (1.2) shows that for such
$p$
, and an application of the relations in (1.2) shows that for such
![]() $p$
,
$p$
,
forcing equality throughout.
2 Base
 $p$
expansions
$p$
expansions
Definition 1. Let
![]() $\unicode[STIX]{x1D706}$
be a nonzero real number in the unit interval. The nonterminating base
$\unicode[STIX]{x1D706}$
be a nonzero real number in the unit interval. The nonterminating base
![]() $p$
expansion of
$p$
expansion of
![]() $\unicode[STIX]{x1D706}$
is the unique expression
$\unicode[STIX]{x1D706}$
is the unique expression
![]() $\unicode[STIX]{x1D706}=\sum _{e\geqslant 1}\unicode[STIX]{x1D706}^{(e)}\cdot p^{-e}$
with the property that the integers
$\unicode[STIX]{x1D706}=\sum _{e\geqslant 1}\unicode[STIX]{x1D706}^{(e)}\cdot p^{-e}$
with the property that the integers
![]() $0\leqslant \unicode[STIX]{x1D706}^{(e)}\leqslant p-1$
are all not eventually zero. The number
$0\leqslant \unicode[STIX]{x1D706}^{(e)}\leqslant p-1$
are all not eventually zero. The number
![]() $\unicode[STIX]{x1D706}^{(e)}$
is called the
$\unicode[STIX]{x1D706}^{(e)}$
is called the
![]() $e$
th digit of
$e$
th digit of
![]() $\unicode[STIX]{x1D706}$
in base
$\unicode[STIX]{x1D706}$
in base
![]() $p$
. By convention, we set
$p$
. By convention, we set
![]() $\unicode[STIX]{x1D706}^{(0)}=0^{(e)}=0$
.
$\unicode[STIX]{x1D706}^{(0)}=0^{(e)}=0$
.
Definition 2. Let
![]() $\unicode[STIX]{x1D706}$
be a nonzero real number in the unit interval, and fix a prime
$\unicode[STIX]{x1D706}$
be a nonzero real number in the unit interval, and fix a prime
![]() $p$
. Given an integer
$p$
. Given an integer
![]() $e\geqslant 1$
, we call
$e\geqslant 1$
, we call
![]() $\langle \unicode[STIX]{x1D706}\rangle _{e}:=\sum _{s=1}^{e}\unicode[STIX]{x1D706}^{(s)}\cdot p^{-s}$
the eth
truncation of
$\langle \unicode[STIX]{x1D706}\rangle _{e}:=\sum _{s=1}^{e}\unicode[STIX]{x1D706}^{(s)}\cdot p^{-s}$
the eth
truncation of
![]() $\unicode[STIX]{x1D706}$
in base
$\unicode[STIX]{x1D706}$
in base
![]() $p$
. By convention, we set
$p$
. By convention, we set
![]() $\left\langle \unicode[STIX]{x1D706}\right\rangle _{0}=\left\langle 0\right\rangle _{e}=0$
. Given a vector
$\left\langle \unicode[STIX]{x1D706}\right\rangle _{0}=\left\langle 0\right\rangle _{e}=0$
. Given a vector
![]() $\boldsymbol{\unicode[STIX]{x1D706}}\in [0,1]^{n}$
, we use
$\boldsymbol{\unicode[STIX]{x1D706}}\in [0,1]^{n}$
, we use
![]() $\left\langle \boldsymbol{\unicode[STIX]{x1D706}}\right\rangle _{e}$
to denote the vector whose entries are the
$\left\langle \boldsymbol{\unicode[STIX]{x1D706}}\right\rangle _{e}$
to denote the vector whose entries are the
![]() $e$
th truncations of the entries of
$e$
th truncations of the entries of
![]() $\boldsymbol{\unicode[STIX]{x1D706}}$
.
$\boldsymbol{\unicode[STIX]{x1D706}}$
.
When
![]() $p$
is obvious from the context (e.g., the characteristic of an ambient field), we omit any reference to the base when discussing digits and truncations.
$p$
is obvious from the context (e.g., the characteristic of an ambient field), we omit any reference to the base when discussing digits and truncations.
Lemma 3. If
![]() $(p^{e}-1)\cdot \unicode[STIX]{x1D706}\in \mathbb{N}$
for some
$(p^{e}-1)\cdot \unicode[STIX]{x1D706}\in \mathbb{N}$
for some
![]() $e$
, then
$e$
, then
![]() $(p^{e}-1)\cdot \unicode[STIX]{x1D706}=p^{e}\cdot \left\langle \unicode[STIX]{x1D706}\right\rangle _{e}$
.
$(p^{e}-1)\cdot \unicode[STIX]{x1D706}=p^{e}\cdot \left\langle \unicode[STIX]{x1D706}\right\rangle _{e}$
.
Proof. This follows from the observation (whose verification is left to the reader) that if
![]() $(p^{e}-1)\cdot \unicode[STIX]{x1D706}\in \mathbb{N}$
, then the digits of
$(p^{e}-1)\cdot \unicode[STIX]{x1D706}\in \mathbb{N}$
, then the digits of
![]() $\unicode[STIX]{x1D706}$
(in base
$\unicode[STIX]{x1D706}$
(in base
![]() $p$
) are periodic and repeat after
$p$
) are periodic and repeat after
![]() $e$
terms.◻
$e$
terms.◻
Lemma 4. If
![]() $\unicode[STIX]{x1D706}\in (0,1]$
, then
$\unicode[STIX]{x1D706}\in (0,1]$
, then
![]() $p^{e}\cdot \left\langle \unicode[STIX]{x1D706}\right\rangle _{e}\in \mathbb{N}$
, and
$p^{e}\cdot \left\langle \unicode[STIX]{x1D706}\right\rangle _{e}\in \mathbb{N}$
, and
![]() $\left\langle \unicode[STIX]{x1D706}\right\rangle _{e}<\unicode[STIX]{x1D706}\leqslant \left\langle \unicode[STIX]{x1D706}\right\rangle _{e}+\frac{1}{p^{e}}$
. Furthermore, if
$\left\langle \unicode[STIX]{x1D706}\right\rangle _{e}<\unicode[STIX]{x1D706}\leqslant \left\langle \unicode[STIX]{x1D706}\right\rangle _{e}+\frac{1}{p^{e}}$
. Furthermore, if
![]() $(p-1)\cdot \unicode[STIX]{x1D706}\in \mathbb{N}$
, then
$(p-1)\cdot \unicode[STIX]{x1D706}\in \mathbb{N}$
, then
![]() $\unicode[STIX]{x1D706}^{(e)}=(p-1)\cdot \unicode[STIX]{x1D706}$
for every
$\unicode[STIX]{x1D706}^{(e)}=(p-1)\cdot \unicode[STIX]{x1D706}$
for every
![]() $e\geqslant 1$
.
$e\geqslant 1$
.
Proof. The first two assertions follow from the definitions. For the third, note that the nonterminating expansion for
![]() $\unicode[STIX]{x1D706}$
can be obtained by multiplying each term in the expansion
$\unicode[STIX]{x1D706}$
can be obtained by multiplying each term in the expansion
![]() $1=\sum _{e\geqslant 1}(p-1)\cdot p^{-e}$
by
$1=\sum _{e\geqslant 1}(p-1)\cdot p^{-e}$
by
![]() $\unicode[STIX]{x1D706}$
.◻
$\unicode[STIX]{x1D706}$
.◻
Definition 5. Let
![]() $(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})\in [0,1]^{n}$
. We say that
$(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})\in [0,1]^{n}$
. We say that
![]() $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n}$
add without carrying (base
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n}$
add without carrying (base
![]() $p$
) if
$p$
) if
![]() ${\unicode[STIX]{x1D706}_{1}}^{(e)}+\cdots +{\unicode[STIX]{x1D706}_{n}}^{(e)}\leqslant p-1$
for every
${\unicode[STIX]{x1D706}_{1}}^{(e)}+\cdots +{\unicode[STIX]{x1D706}_{n}}^{(e)}\leqslant p-1$
for every
![]() $e\geqslant 1$
.
$e\geqslant 1$
.
The notion of adding without carrying is relevant in light of the following classical result.
Lemma 6. [Reference DicksonDic02, Reference LucasLuc78]
Fix
![]() $\mathbf{k}=\left(k_{1},\ldots ,k_{n}\right)\in \mathbb{N}^{n}$
, and set
$\mathbf{k}=\left(k_{1},\ldots ,k_{n}\right)\in \mathbb{N}^{n}$
, and set
![]() $N=k_{1}+\cdots +k_{n}$
. For every
$N=k_{1}+\cdots +k_{n}$
. For every
![]() $i$
, let
$i$
, let
![]() $k_{i}=\sum _{e\geqslant 0}k_{i,e}\cdot p^{e}$
denote the (unique) base
$k_{i}=\sum _{e\geqslant 0}k_{i,e}\cdot p^{e}$
denote the (unique) base
![]() $p$
expansion of the integer
$p$
expansion of the integer
![]() $k_{i}$
(so that
$k_{i}$
(so that
![]() $k_{i,e}=0$
for
$k_{i,e}=0$
for
![]() $e\gg 0$
), and, similarly, let
$e\gg 0$
), and, similarly, let
![]() $N=\sum _{e\geqslant 0}N_{e}\cdot p^{e}$
denote the (unique) base
$N=\sum _{e\geqslant 0}N_{e}\cdot p^{e}$
denote the (unique) base
![]() $p$
expansion of
$p$
expansion of
![]() $N$
. Then, the multinomial coefficient
$N$
. Then, the multinomial coefficient
![]() $\binom{N}{\mathbf{k}}:=\frac{N!}{k_{1}!\cdots k_{n}!}\not \equiv 0~\text{mod}~p$
if and only if
$\binom{N}{\mathbf{k}}:=\frac{N!}{k_{1}!\cdots k_{n}!}\not \equiv 0~\text{mod}~p$
if and only if
![]() $k_{1,e}+\cdots +k_{n,e}=N_{e}$
for every
$k_{1,e}+\cdots +k_{n,e}=N_{e}$
for every
![]() $e\geqslant 0$
.
$e\geqslant 0$
.
Corollary 7. The entries of a vector
![]() $(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})\in [0,1]^{n}$
add without carrying if and only if
$(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})\in [0,1]^{n}$
add without carrying if and only if
![]() $\binom{p^{e}\left\langle \unicode[STIX]{x1D706}_{1}\right\rangle _{e}+\cdots +p^{e}\left\langle \unicode[STIX]{x1D706}_{n}\right\rangle _{e}}{p^{e}\left\langle \unicode[STIX]{x1D706}_{1}\right\rangle _{e},\ldots ,p^{e}\left\langle \unicode[STIX]{x1D706}_{n}\right\rangle _{e}}\not \equiv 0~\text{mod}~p$
for every
$\binom{p^{e}\left\langle \unicode[STIX]{x1D706}_{1}\right\rangle _{e}+\cdots +p^{e}\left\langle \unicode[STIX]{x1D706}_{n}\right\rangle _{e}}{p^{e}\left\langle \unicode[STIX]{x1D706}_{1}\right\rangle _{e},\ldots ,p^{e}\left\langle \unicode[STIX]{x1D706}_{n}\right\rangle _{e}}\not \equiv 0~\text{mod}~p$
for every
![]() $e\geqslant 1$
(or, equivalently, for infinitely many
$e\geqslant 1$
(or, equivalently, for infinitely many
![]() $e\geqslant 1$
).
$e\geqslant 1$
).
Proof. Lemma 6 implies that
![]() $\binom{p^{e}\left\langle \unicode[STIX]{x1D706}_{1}\right\rangle _{e}+\cdots +p^{e}\left\langle \unicode[STIX]{x1D706}_{n}\right\rangle _{e}}{p^{e}\left\langle \unicode[STIX]{x1D706}_{1}\right\rangle _{e},\ldots ,p^{e}\left\langle \unicode[STIX]{x1D706}_{n}\right\rangle _{e}}\not \equiv 0~\text{mod}~p\;\Longleftrightarrow \;{\unicode[STIX]{x1D706}_{1}}^{(s)}+\cdots +{\unicode[STIX]{x1D706}_{n}}^{(s)}\leqslant p-1$
for every
$\binom{p^{e}\left\langle \unicode[STIX]{x1D706}_{1}\right\rangle _{e}+\cdots +p^{e}\left\langle \unicode[STIX]{x1D706}_{n}\right\rangle _{e}}{p^{e}\left\langle \unicode[STIX]{x1D706}_{1}\right\rangle _{e},\ldots ,p^{e}\left\langle \unicode[STIX]{x1D706}_{n}\right\rangle _{e}}\not \equiv 0~\text{mod}~p\;\Longleftrightarrow \;{\unicode[STIX]{x1D706}_{1}}^{(s)}+\cdots +{\unicode[STIX]{x1D706}_{n}}^{(s)}\leqslant p-1$
for every
![]() $1\leqslant s\leqslant e$
, and the claim follows.◻
$1\leqslant s\leqslant e$
, and the claim follows.◻
Lemma 8. Let
![]() $(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})\in \mathbb{Q}^{n}\cap [0,1]^{n}$
.
$(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})\in \mathbb{Q}^{n}\cap [0,1]^{n}$
.
-
(1) If
 $\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{n}\leqslant 1$
, then
$\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{n}\leqslant 1$
, then
 $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n}$
add without carrying for infinitely many
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n}$
add without carrying for infinitely many
 $p$
.
$p$
. -
(2) If
 $\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{n}>1$
, then
$\unicode[STIX]{x1D706}_{1}+\cdots +\unicode[STIX]{x1D706}_{n}>1$
, then
 ${\unicode[STIX]{x1D706}_{1}}^{(1)}+\cdots +{\unicode[STIX]{x1D706}_{n}}^{(1)}\geqslant p$
whenever
${\unicode[STIX]{x1D706}_{1}}^{(1)}+\cdots +{\unicode[STIX]{x1D706}_{n}}^{(1)}\geqslant p$
whenever
 $p\gg 0$
.
$p\gg 0$
.
Proof. By Dirichlet’s theorem,
![]() $(p-1)\cdot (\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})\in \mathbb{N}^{n}$
for infinitely many
$(p-1)\cdot (\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})\in \mathbb{N}^{n}$
for infinitely many
![]() $p$
. For such
$p$
. For such
![]() $p$
, Lemma 4 shows that
$p$
, Lemma 4 shows that
![]() ${\unicode[STIX]{x1D706}_{i}}^{(e)}=(p-1)\cdot \unicode[STIX]{x1D706}_{i}$
for each
${\unicode[STIX]{x1D706}_{i}}^{(e)}=(p-1)\cdot \unicode[STIX]{x1D706}_{i}$
for each
![]() $i$
and
$i$
and
![]() $e$
, and therefore
$e$
, and therefore
![]() $\sum {\unicode[STIX]{x1D706}_{i}}^{(e)}=(p-1)\cdot \sum \unicode[STIX]{x1D706}_{i}$
, which establishes the first point. For the second point, note that
$\sum {\unicode[STIX]{x1D706}_{i}}^{(e)}=(p-1)\cdot \sum \unicode[STIX]{x1D706}_{i}$
, which establishes the first point. For the second point, note that
where the last inequality follows from Lemma 4. Consequently,
and, hence,
![]() $\sum {\unicode[STIX]{x1D706}_{i}}^{(1)}\geqslant p$
whenever
$\sum {\unicode[STIX]{x1D706}_{i}}^{(1)}\geqslant p$
whenever
![]() $p\cdot \left(\sum \unicode[STIX]{x1D706}_{i}-1\right)\geqslant n$
.◻
$p\cdot \left(\sum \unicode[STIX]{x1D706}_{i}-1\right)\geqslant n$
.◻
3
 $F$
-pure thresholds
$F$
-pure thresholds
Let
![]() $R$
denote a polynomial ring over a field of characteristic
$R$
denote a polynomial ring over a field of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $\mathfrak{m}=(x_{1},\ldots ,x_{m})$
denote the homogeneous maximal ideal of
$\mathfrak{m}=(x_{1},\ldots ,x_{m})$
denote the homogeneous maximal ideal of
![]() $R$
. For every ideal
$R$
. For every ideal
![]() $I$
of
$I$
of
![]() $R$
, let
$R$
, let
![]() $I^{[p^{e}]}$
denote the ideal generated by the set
$I^{[p^{e}]}$
denote the ideal generated by the set
![]() $\{f^{p^{e}}:f\in I\}$
. We call
$\{f^{p^{e}}:f\in I\}$
. We call
![]() $I^{[p^{e}]}$
the
$I^{[p^{e}]}$
the
![]() $e$
th Frobenius power of
$e$
th Frobenius power of
![]() $I$
.
$I$
.
Definition 9. [Reference Takagi and WatanabeTW04, Reference Mustaţǎ, Takagi and WatanabeMTW05] Fix a nonzero ideal
![]() $\mathfrak{a}\subseteq \mathfrak{m}$
generated by
$\mathfrak{a}\subseteq \mathfrak{m}$
generated by
![]() $t$
elements. By the pigeon-hole principle, we have that
$t$
elements. By the pigeon-hole principle, we have that
![]() $\mathfrak{a}^{t(p^{e}-1)+1}\subseteq \mathfrak{m}^{[p^{e}]}$
, and hence
$\mathfrak{a}^{t(p^{e}-1)+1}\subseteq \mathfrak{m}^{[p^{e}]}$
, and hence
is a well-defined integer, bounded above by
![]() $t(p^{e}-1)+1$
. Thus, the sequence
$t(p^{e}-1)+1$
. Thus, the sequence
![]() $\{p^{-e}\cdot \unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)\}$
is bounded above by
$\{p^{-e}\cdot \unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)\}$
is bounded above by
![]() $t$
, and the flatness of the Frobenius morphism can be used to show that this sequence is nondecreasing, so that the limit
$t$
, and the flatness of the Frobenius morphism can be used to show that this sequence is nondecreasing, so that the limit
exists. We call this limit the
![]() $F$
-pure threshold of
$F$
-pure threshold of
![]() $\mathfrak{a}$
at the origin. In the case that
$\mathfrak{a}$
at the origin. In the case that
![]() $\mathfrak{a}$
is a principal ideal generated by a polynomial
$\mathfrak{a}$
is a principal ideal generated by a polynomial
![]() $f\in \mathfrak{m}$
, we write
$f\in \mathfrak{m}$
, we write
![]() $\mathbf{fpt}(f)$
instead of
$\mathbf{fpt}(f)$
instead of
![]() $\mathbf{fpt}(\mathfrak{a})$
.
$\mathbf{fpt}(\mathfrak{a})$
.
Remark 10. Although it is not obvious from the definition, the
![]() $F$
-pure threshold is a rational number (see [Reference Blickle, Mustaţǎ and SmithBMS08, Theorem 3.1]).
$F$
-pure threshold is a rational number (see [Reference Blickle, Mustaţǎ and SmithBMS08, Theorem 3.1]).
Remark 11. As
![]() $\mathfrak{a}\neq 0$
, we have that
$\mathfrak{a}\neq 0$
, we have that
![]() $\mathfrak{a}\not \subseteq \mathfrak{m}^{[p^{e}]}$
for large values of
$\mathfrak{a}\not \subseteq \mathfrak{m}^{[p^{e}]}$
for large values of
![]() $e$
, so that
$e$
, so that
![]() $\unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)\neq 0$
for
$\unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)\neq 0$
for
![]() $e\gg 0$
, and hence
$e\gg 0$
, and hence
![]() $\mathbf{fpt}(\mathfrak{a})\neq 0$
. Moreover, the bound
$\mathbf{fpt}(\mathfrak{a})\neq 0$
. Moreover, the bound
![]() $\unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)\leqslant t(p^{e}-1)+1$
shows that
$\unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)\leqslant t(p^{e}-1)+1$
shows that
![]() $\mathbf{fpt}(\mathfrak{a})\leqslant t$
. In particular, when
$\mathbf{fpt}(\mathfrak{a})\leqslant t$
. In particular, when
![]() $\mathfrak{a}=(f)$
is principal, we have that
$\mathfrak{a}=(f)$
is principal, we have that
![]() $\mathbf{fpt}(f)\in (0,1]$
.
$\mathbf{fpt}(f)\in (0,1]$
.
Remark 12. If
![]() $\mathfrak{a}\subseteq \mathfrak{b}$
are ideals contained in
$\mathfrak{a}\subseteq \mathfrak{b}$
are ideals contained in
![]() $\mathfrak{m}$
, then
$\mathfrak{m}$
, then
![]() $\unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)\leqslant \unicode[STIX]{x1D708}_{\mathfrak{b}}\left(p^{e}\right)$
, and hence
$\unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)\leqslant \unicode[STIX]{x1D708}_{\mathfrak{b}}\left(p^{e}\right)$
, and hence
![]() $\mathbf{fpt}(\mathfrak{a})\leqslant \mathbf{fpt}(\mathfrak{b})$
. In particular, if
$\mathbf{fpt}(\mathfrak{a})\leqslant \mathbf{fpt}(\mathfrak{b})$
. In particular, if
![]() $f\in \mathfrak{m}$
is a polynomial and
$f\in \mathfrak{m}$
is a polynomial and
![]() $\mathfrak{a}_{f}$
is its term ideal, then
$\mathfrak{a}_{f}$
is its term ideal, then
The following lemma, which is well known to experts, plays a key role in this article.
Lemma 13. Let
![]() $\unicode[STIX]{x1D706}\in (0,1]$
be a rational number such that
$\unicode[STIX]{x1D706}\in (0,1]$
be a rational number such that
![]() $(p^{e}-1)\cdot \unicode[STIX]{x1D706}\in \mathbb{N}$
for some
$(p^{e}-1)\cdot \unicode[STIX]{x1D706}\in \mathbb{N}$
for some
![]() $e\geqslant 1$
. Then,
$e\geqslant 1$
. Then,
![]() $\mathbf{fpt}(f)\geqslant \unicode[STIX]{x1D706}$
if and only if
$\mathbf{fpt}(f)\geqslant \unicode[STIX]{x1D706}$
if and only if
![]() $f^{(p^{e}-1)\cdot \unicode[STIX]{x1D706}}\notin \mathfrak{m}^{[p^{e}]}$
.
$f^{(p^{e}-1)\cdot \unicode[STIX]{x1D706}}\notin \mathfrak{m}^{[p^{e}]}$
.
Proof. This may be deduced, for example, from either [Reference SchwedeSch08, Proposition 3.3] and [Reference SchwedeSch08, Lemma 5.2], [Reference HernándezHer12, Key Lemma 3.1] and [Reference HernándezHer12, Proposition 4.2], or [Reference Mustaţǎ, Takagi and WatanabeMTW05, Proposition 1.9] and [Reference Blickle, Mustaţă and SmithBMS09, Proposition 4.3(ii)]. For the convenience of the reader, we present a proof based on the last of these options (as it only involves concepts introduced herein), and we begin by recalling the relevant facts. In what follows, we fix an integer
![]() $e\geqslant 1$
.
$e\geqslant 1$
.
-
(1)
 $\unicode[STIX]{x1D708}_{f}\left(p^{e}\right)=\left\lceil p^{e}\cdot \mathbf{fpt}(f)\right\rceil -1$
(see [Reference Mustaţǎ, Takagi and WatanabeMTW05, Proposition 1.9]).
$\unicode[STIX]{x1D708}_{f}\left(p^{e}\right)=\left\lceil p^{e}\cdot \mathbf{fpt}(f)\right\rceil -1$
(see [Reference Mustaţǎ, Takagi and WatanabeMTW05, Proposition 1.9]). -
(2) If
 $a\in \mathbb{N}$
, and if
$a\in \mathbb{N}$
, and if
 $\mathbf{fpt}(f)>\frac{a}{p^{e}}$
, then
$\mathbf{fpt}(f)>\frac{a}{p^{e}}$
, then
 $\mathbf{fpt}(f)\geqslant \frac{a}{p^{e}-1}$
(see [Reference Blickle, Mustaţă and SmithBMS09, Proposition 4.3(ii)]).
$\mathbf{fpt}(f)\geqslant \frac{a}{p^{e}-1}$
(see [Reference Blickle, Mustaţă and SmithBMS09, Proposition 4.3(ii)]).
Note that, as
![]() $\left\lceil \unicode[STIX]{x1D6FC}\right\rceil <\unicode[STIX]{x1D6FC}+1$
for every real number
$\left\lceil \unicode[STIX]{x1D6FC}\right\rceil <\unicode[STIX]{x1D6FC}+1$
for every real number
![]() $\unicode[STIX]{x1D6FC}$
, (1) above implies that
$\unicode[STIX]{x1D6FC}$
, (1) above implies that
-
(3)
 $\unicode[STIX]{x1D708}_{f}\left(p^{e}\right)<p^{e}\cdot \mathbf{fpt}(f)$
.
$\unicode[STIX]{x1D708}_{f}\left(p^{e}\right)<p^{e}\cdot \mathbf{fpt}(f)$
.
We now begin our proof. First, note that the assumption that
![]() $(p^{e}-1)\unicode[STIX]{x1D706}\in \mathbb{N}$
implies that
$(p^{e}-1)\unicode[STIX]{x1D706}\in \mathbb{N}$
implies that
If
![]() $\mathbf{fpt}(f)\geqslant \unicode[STIX]{x1D706}$
, then combining (3.1) and (1) above shows that
$\mathbf{fpt}(f)\geqslant \unicode[STIX]{x1D706}$
, then combining (3.1) and (1) above shows that
On the other hand, if
![]() $(p^{e}-1)\cdot \unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D708}_{f}\left(p^{e}\right)$
, then combing this with (3) above implies that
$(p^{e}-1)\cdot \unicode[STIX]{x1D706}\leqslant \unicode[STIX]{x1D708}_{f}\left(p^{e}\right)$
, then combing this with (3) above implies that
and (2) above then shows that
![]() $\mathbf{fpt}(f)\geqslant \frac{(p^{e}-1)\cdot \unicode[STIX]{x1D706}}{p^{e}-1}=\unicode[STIX]{x1D706}$
.
$\mathbf{fpt}(f)\geqslant \frac{(p^{e}-1)\cdot \unicode[STIX]{x1D706}}{p^{e}-1}=\unicode[STIX]{x1D706}$
.
In summary, we have just shown that
![]() $\mathbf{fpt}(f)\geqslant \unicode[STIX]{x1D706}$
if and only if
$\mathbf{fpt}(f)\geqslant \unicode[STIX]{x1D706}$
if and only if
![]() $\unicode[STIX]{x1D708}_{f}\left(p^{e}\right)\geqslant (p^{e}-1)\cdot \unicode[STIX]{x1D706}$
, and the claim then follows.◻
$\unicode[STIX]{x1D708}_{f}\left(p^{e}\right)\geqslant (p^{e}-1)\cdot \unicode[STIX]{x1D706}$
, and the claim then follows.◻
4 Polyhedral constructions
In this section, we consider two key polyhedra associated to polynomials, and we begin by recalling some basic notions from convex geometry. Throughout this discussion, our main reference is [Reference WebsterWeb94].
4.1 Polyhedral sets
Given a linear form
![]() $L\in \mathbb{R}[z_{1},\ldots ,z_{m}]$
and a real number
$L\in \mathbb{R}[z_{1},\ldots ,z_{m}]$
and a real number
![]() $\unicode[STIX]{x1D6FD}$
, we use
$\unicode[STIX]{x1D6FD}$
, we use
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}^{L}$
to denote the hyperplane
$\text{H}_{\unicode[STIX]{x1D6FD}}^{L}$
to denote the hyperplane
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}^{L}=\{\mathbf{\text{v}}\in \mathbb{R}^{m}:L(\mathbf{\text{v}})=\unicode[STIX]{x1D6FD}\}$
, and we use
$\text{H}_{\unicode[STIX]{x1D6FD}}^{L}=\{\mathbf{\text{v}}\in \mathbb{R}^{m}:L(\mathbf{\text{v}})=\unicode[STIX]{x1D6FD}\}$
, and we use
![]() $\overline{\text{HS}}_{\unicode[STIX]{x1D6FD}}^{L}$
to denote the closed upper halfspace
$\overline{\text{HS}}_{\unicode[STIX]{x1D6FD}}^{L}$
to denote the closed upper halfspace
![]() $\overline{\text{HS}}_{\unicode[STIX]{x1D6FD}}^{L}=\{\mathbf{\text{v}}\in \mathbb{R}^{m}:L(\mathbf{\text{v}})\geqslant \unicode[STIX]{x1D6FD}\}$
. Given
$\overline{\text{HS}}_{\unicode[STIX]{x1D6FD}}^{L}=\{\mathbf{\text{v}}\in \mathbb{R}^{m}:L(\mathbf{\text{v}})\geqslant \unicode[STIX]{x1D6FD}\}$
. Given
![]() $\mathscr{P}\subseteq \mathbb{R}^{m}$
,
$\mathscr{P}\subseteq \mathbb{R}^{m}$
,
![]() $\overline{\text{HS}}_{\unicode[STIX]{x1D6FD}}^{L}$
is called a supporting halfspace of
$\overline{\text{HS}}_{\unicode[STIX]{x1D6FD}}^{L}$
is called a supporting halfspace of
![]() $\mathscr{P}$
if
$\mathscr{P}$
if
![]() $\mathscr{P}\subseteq \overline{\text{HS}}_{\unicode[STIX]{x1D6FD}}^{L}$
and
$\mathscr{P}\subseteq \overline{\text{HS}}_{\unicode[STIX]{x1D6FD}}^{L}$
and
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathscr{P}\neq \emptyset$
. In this case,
$\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathscr{P}\neq \emptyset$
. In this case,
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathscr{P}$
is called an (exposed) face of
$\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathscr{P}$
is called an (exposed) face of
![]() $\mathscr{P}$
. Recall that a subset
$\mathscr{P}$
. Recall that a subset
![]() $\mathscr{P}\subseteq \mathbb{R}^{m}$
is called a polyhedral set if there exist finitely many linear forms
$\mathscr{P}\subseteq \mathbb{R}^{m}$
is called a polyhedral set if there exist finitely many linear forms
![]() $L_{1},\ldots L_{d}$
in
$L_{1},\ldots L_{d}$
in
![]() $\mathbb{R}[z_{1},\ldots ,z_{m}]$
and elements
$\mathbb{R}[z_{1},\ldots ,z_{m}]$
and elements
![]() $\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{d}\in \mathbb{R}$
such that
$\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{d}\in \mathbb{R}$
such that
If we may choose the linear forms
![]() $L_{1},\ldots ,L_{d}$
to have rational coefficients, and the numbers
$L_{1},\ldots ,L_{d}$
to have rational coefficients, and the numbers
![]() $\unicode[STIX]{x1D6FD}_{1},\ldots \unicode[STIX]{x1D6FD}_{d}$
to be rational, then we call the polyhedral set
$\unicode[STIX]{x1D6FD}_{1},\ldots \unicode[STIX]{x1D6FD}_{d}$
to be rational, then we call the polyhedral set
![]() $\mathscr{P}$
rational. In the case that a polyhedral set is rational, all of its faces may described by rational data. A compact polyhedral set is called a polytope.
$\mathscr{P}$
rational. In the case that a polyhedral set is rational, all of its faces may described by rational data. A compact polyhedral set is called a polytope.
Given any subset
![]() $\mathscr{C}\subseteq \mathbb{R}^{m}$
, we use
$\mathscr{C}\subseteq \mathbb{R}^{m}$
, we use
![]() $\text{cone}(\mathscr{C})$
to denote the collection of all finite sums
$\text{cone}(\mathscr{C})$
to denote the collection of all finite sums
![]() $\sum _{\mathbf{v}}\unicode[STIX]{x1D706}_{\mathbf{v}}\cdot \mathbf{v}$
with
$\sum _{\mathbf{v}}\unicode[STIX]{x1D706}_{\mathbf{v}}\cdot \mathbf{v}$
with
![]() $\mathbf{\text{v}}\in \mathscr{C}$
such that
$\mathbf{\text{v}}\in \mathscr{C}$
such that
![]() $\unicode[STIX]{x1D706}_{\mathbf{v}}\geqslant 0$
; we call
$\unicode[STIX]{x1D706}_{\mathbf{v}}\geqslant 0$
; we call
![]() $\text{cone}(\mathscr{C})$
the cone generated by
$\text{cone}(\mathscr{C})$
the cone generated by
![]() $\mathscr{C}$
. Given
$\mathscr{C}$
. Given
![]() $\mathbf{v}\in \mathbb{R}^{m}$
, we call
$\mathbf{v}\in \mathbb{R}^{m}$
, we call
![]() $\text{cone}(\{\mathbf{v}\})$
the ray generated by
$\text{cone}(\{\mathbf{v}\})$
the ray generated by
![]() $\mathbf{v}$
. We also use
$\mathbf{v}$
. We also use
![]() $\text{convex}(\mathscr{C})$
to denote the collection of all finite sums
$\text{convex}(\mathscr{C})$
to denote the collection of all finite sums
![]() $\sum _{\mathbf{v}}\unicode[STIX]{x1D706}_{\mathbf{v}}\cdot \mathbf{v}$
with
$\sum _{\mathbf{v}}\unicode[STIX]{x1D706}_{\mathbf{v}}\cdot \mathbf{v}$
with
![]() $\mathbf{\text{v}}\in \mathscr{C}$
such that
$\mathbf{\text{v}}\in \mathscr{C}$
such that
![]() $\unicode[STIX]{x1D706}_{\mathbf{v}}\geqslant 0$
and
$\unicode[STIX]{x1D706}_{\mathbf{v}}\geqslant 0$
and
![]() $\sum _{\mathbf{v}}\unicode[STIX]{x1D706}_{\mathbf{v}}=1$
; we call
$\sum _{\mathbf{v}}\unicode[STIX]{x1D706}_{\mathbf{v}}=1$
; we call
![]() $\text{convex}(\mathscr{C})$
the convex hull of
$\text{convex}(\mathscr{C})$
the convex hull of
![]() $\mathscr{C}$
. Although it is not obvious from these definitions, both
$\mathscr{C}$
. Although it is not obvious from these definitions, both
![]() $\text{cone}(\mathscr{C})$
and
$\text{cone}(\mathscr{C})$
and
![]() $\text{convex}(\mathscr{C})$
are rational polyhedral sets whenever
$\text{convex}(\mathscr{C})$
are rational polyhedral sets whenever
![]() $\mathscr{C}\subseteq \mathbb{Q}^{m}$
(see [Reference WebsterWeb94, Theorems 4.1.1 and 3.2.5]). Given two subsets
$\mathscr{C}\subseteq \mathbb{Q}^{m}$
(see [Reference WebsterWeb94, Theorems 4.1.1 and 3.2.5]). Given two subsets
![]() $V$
and
$V$
and
![]() $W$
of
$W$
of
![]() $\mathbb{R}^{m}$
, we use
$\mathbb{R}^{m}$
, we use
![]() $V+W$
to denote
$V+W$
to denote
![]() $\{\mathbf{v}+\mathbf{w}:\mathbf{v}\in V,\mathbf{w}\in W\}$
, the Minkowski sum of
$\{\mathbf{v}+\mathbf{w}:\mathbf{v}\in V,\mathbf{w}\in W\}$
, the Minkowski sum of
![]() $V$
and
$V$
and
![]() $W$
. We conclude by recalling the following structural result (often called the finite-basis theorem for polyhedra): a set in
$W$
. We conclude by recalling the following structural result (often called the finite-basis theorem for polyhedra): a set in
![]() $\mathbb{R}^{m}$
is polyhedral if and only if it is of the form
$\mathbb{R}^{m}$
is polyhedral if and only if it is of the form
![]() $\text{convex}(\mathscr{C})+\text{cone}(\mathscr{D})$
, where
$\text{convex}(\mathscr{C})+\text{cone}(\mathscr{D})$
, where
![]() $\mathscr{C}$
and
$\mathscr{C}$
and
![]() $\mathscr{D}$
are two finite (and possibly empty) subsets of
$\mathscr{D}$
are two finite (and possibly empty) subsets of
![]() $\mathbb{R}^{m}$
, and is rational if and only if
$\mathbb{R}^{m}$
, and is rational if and only if
![]() $\mathscr{C}$
and
$\mathscr{C}$
and
![]() $\mathscr{D}$
are contained in
$\mathscr{D}$
are contained in
![]() $\mathbb{Q}^{m}$
(see [Reference WebsterWeb94, Theorem 4.1.2]).
$\mathbb{Q}^{m}$
(see [Reference WebsterWeb94, Theorem 4.1.2]).
Remark 14. By the finite-basis theorem for polyhedra, every polyhedron
![]() $\mathscr{P}\subseteq \mathbb{R}^{m}$
is of the form
$\mathscr{P}\subseteq \mathbb{R}^{m}$
is of the form
![]() $\text{convex}(\mathscr{C})+\text{cone}(\mathscr{D})$
for some finite subsets
$\text{convex}(\mathscr{C})+\text{cone}(\mathscr{D})$
for some finite subsets
![]() $\mathscr{C},\mathscr{D}\subseteq \mathbb{R}_{{\geqslant}0}^{m}$
. It then follows from the finiteness of
$\mathscr{C},\mathscr{D}\subseteq \mathbb{R}_{{\geqslant}0}^{m}$
. It then follows from the finiteness of
![]() $\mathscr{C}$
(and, hence, the boundedness of
$\mathscr{C}$
(and, hence, the boundedness of
![]() $\text{convex}(\mathscr{C})$
) that the polyhedron
$\text{convex}(\mathscr{C})$
) that the polyhedron
![]() $\mathscr{P}$
is unbounded if and only if it contains a ray of the form
$\mathscr{P}$
is unbounded if and only if it contains a ray of the form
![]() $\mathbf{v}+\unicode[STIX]{x1D706}\cdot \mathbf{w}$
, with
$\mathbf{v}+\unicode[STIX]{x1D706}\cdot \mathbf{w}$
, with
![]() $\mathbf{v}\in \mathscr{P}$
, and
$\mathbf{v}\in \mathscr{P}$
, and
![]() $\mathbf{0}\neq \mathbf{w}\in \mathbb{R}^{m}$
.
$\mathbf{0}\neq \mathbf{w}\in \mathbb{R}^{m}$
.
4.2 Splitting polytopes
Notation 15. For
![]() $\mathbf{s}=(s_{1},\ldots ,s_{n})\in \mathbb{R}^{n}$
,
$\mathbf{s}=(s_{1},\ldots ,s_{n})\in \mathbb{R}^{n}$
,
![]() $|\mathbf{s}|$
denotes the coordinate sum
$|\mathbf{s}|$
denotes the coordinate sum
![]() $s_{1}+\cdots +s_{n}$
. We stress that
$s_{1}+\cdots +s_{n}$
. We stress that
![]() $|\cdot |$
is not the usual Euclidean norm on
$|\cdot |$
is not the usual Euclidean norm on
![]() $\mathbb{R}^{n}$
. Furthermore, when dealing with elements of
$\mathbb{R}^{n}$
. Furthermore, when dealing with elements of
![]() $\mathbb{R}^{n}$
, we use
$\mathbb{R}^{n}$
, we use
![]() $\prec$
and
$\prec$
and
![]() $\preccurlyeq$
to denote component-wise (strict) inequality. Finally,
$\preccurlyeq$
to denote component-wise (strict) inequality. Finally,
![]() $\mathbf{1}_{m}$
denotes the element
$\mathbf{1}_{m}$
denotes the element
![]() $(1,\ldots ,1)\in \mathbb{R}^{m}$
.
$(1,\ldots ,1)\in \mathbb{R}^{m}$
.
Notation 16. Fix a polynomial ring
![]() $\mathbb{L}[x_{1},\ldots ,x_{m}]$
over a field of arbitrary characteristic. Given a vector
$\mathbb{L}[x_{1},\ldots ,x_{m}]$
over a field of arbitrary characteristic. Given a vector
![]() $\mathbf{a}=(a_{1},\ldots ,a_{m})\in \mathbb{N}^{m}$
, we use
$\mathbf{a}=(a_{1},\ldots ,a_{m})\in \mathbb{N}^{m}$
, we use
![]() $x^{\mathbf{a}}$
to denote the monomial
$x^{\mathbf{a}}$
to denote the monomial
![]() $x_{1}^{a_{1}}\cdots x_{m}^{a_{m}}$
. If
$x_{1}^{a_{1}}\cdots x_{m}^{a_{m}}$
. If
![]() $f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
is the unique expression of a polynomial
$f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
is the unique expression of a polynomial
![]() $f$
as an
$f$
as an
![]() $\mathbb{L}^{\ast }$
-linear combination of distinct monomials, then we use
$\mathbb{L}^{\ast }$
-linear combination of distinct monomials, then we use
![]() $\text{Supp}(f)$
to denote
$\text{Supp}(f)$
to denote
![]() $\{x^{\mathbf{a}_{1}},\ldots ,x^{\mathbf{a}_{n}}\}$
, the collection of supporting monomials of
$\{x^{\mathbf{a}_{1}},\ldots ,x^{\mathbf{a}_{n}}\}$
, the collection of supporting monomials of
![]() $f$
. We often abuse notation by identifying monomials with their exponent vectors, and thus often write
$f$
. We often abuse notation by identifying monomials with their exponent vectors, and thus often write
![]() $\text{Supp}(f)=\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\}$
. We continue to use
$\text{Supp}(f)=\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\}$
. We continue to use
![]() $\mathfrak{a}_{f}$
to denote the term ideal of
$\mathfrak{a}_{f}$
to denote the term ideal of
![]() $f$
, that is, the monomial ideal generated by
$f$
, that is, the monomial ideal generated by
![]() $\text{Supp}(f)$
in
$\text{Supp}(f)$
in
![]() $\mathbb{L}[x_{1},\ldots ,x_{m}]$
.
$\mathbb{L}[x_{1},\ldots ,x_{m}]$
.
Definition 17. Fix an arbitrary field
![]() $\mathbb{L}$
, and consider a polynomial
$\mathbb{L}$
, and consider a polynomial
![]() $f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin, with
$f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin, with
![]() $\text{Supp}(f)=\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\}\subseteq \mathbb{N}^{m}$
.
$\text{Supp}(f)=\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\}\subseteq \mathbb{N}^{m}$
.
-
(1) We call the
 $m\times n$
matrix
$m\times n$
matrix
 $\mathbf{E}:=\left[\mathbf{a}_{1}\cdots \mathbf{a}_{n}\right]$
the exponent matrix of
$\mathbf{E}:=\left[\mathbf{a}_{1}\cdots \mathbf{a}_{n}\right]$
the exponent matrix of
 $f$
.
$f$
. -
(2) We call
 $\mathbf{P}:=\{\mathbf{s}\in \mathbb{R}_{{\geqslant}0}^{n}:\mathbf{E}\mathbf{s}\preccurlyeq \mathbf{1}_{m}\}$
the splitting polytope of
$\mathbf{P}:=\{\mathbf{s}\in \mathbb{R}_{{\geqslant}0}^{n}:\mathbf{E}\mathbf{s}\preccurlyeq \mathbf{1}_{m}\}$
the splitting polytope of
 $f$
.
$f$
.
Remark 18. The exponent matrix and splitting polytope associated to
![]() $f$
depend only on
$f$
depend only on
![]() $\text{Supp}(f)$
. Moreover, it follows by definition that
$\text{Supp}(f)$
. Moreover, it follows by definition that
![]() $\mathbf{P}$
is a polyhedral set, and as
$\mathbf{P}$
is a polyhedral set, and as
![]() $\mathbf{E}$
has nonnegative integer entries,
$\mathbf{E}$
has nonnegative integer entries,
![]() $\mathbf{P}$
is a compact subset (and, hence, polytope) in
$\mathbf{P}$
is a compact subset (and, hence, polytope) in
![]() $[0,1]^{n}$
.
$[0,1]^{n}$
.
Definition 19. Consider the linear functional
![]() $\mathbb{R}^{n}\rightarrow \mathbb{R}$
given by
$\mathbb{R}^{n}\rightarrow \mathbb{R}$
given by
![]() $\mathbf{s}\mapsto |\mathbf{s}|=s_{1}+\cdots +s_{n}$
. As
$\mathbf{s}\mapsto |\mathbf{s}|=s_{1}+\cdots +s_{n}$
. As
![]() $\mathbf{P}$
is compact,
$\mathbf{P}$
is compact,
![]() $\unicode[STIX]{x1D6FD}=\max \{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\}$
is well defined, and the nonempty set
$\unicode[STIX]{x1D6FD}=\max \{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\}$
is well defined, and the nonempty set
![]() $\{\mathbf{s}\in \mathbf{P}:|\mathbf{s}|=\unicode[STIX]{x1D6FD}\}$
defines an exposed face of
$\{\mathbf{s}\in \mathbf{P}:|\mathbf{s}|=\unicode[STIX]{x1D6FD}\}$
defines an exposed face of
![]() $\mathbf{P}$
. We call this face the maximal face of
$\mathbf{P}$
. We call this face the maximal face of
![]() $\mathbf{P}$
, and denote it by
$\mathbf{P}$
, and denote it by
![]() $\mathbf{P}_{\text{max}}$
.
$\mathbf{P}_{\text{max}}$
.
Example 20. If
![]() $f=x_{1}^{d_{1}}+\cdots +x_{m}^{d_{m}}$
, then
$f=x_{1}^{d_{1}}+\cdots +x_{m}^{d_{m}}$
, then
![]() $\mathbf{P}=\{\mathbf{s}\in \mathbb{R}^{m}:\mathbf{0}\preccurlyeq \mathbf{s}\preccurlyeq (1/d_{1},\ldots ,1/d_{m})\}$
, and
$\mathbf{P}=\{\mathbf{s}\in \mathbb{R}^{m}:\mathbf{0}\preccurlyeq \mathbf{s}\preccurlyeq (1/d_{1},\ldots ,1/d_{m})\}$
, and
![]() $\mathbf{P}_{\text{max}}$
consists of the single point
$\mathbf{P}_{\text{max}}$
consists of the single point
![]() $\left(1/d_{1},\ldots ,1/d_{m}\right)$
.
$\left(1/d_{1},\ldots ,1/d_{m}\right)$
.
The splitting polytopes considered in the following examples are depicted in figure 1.
Example 21. If
![]() $f=x^{a}+y^{b}+x^{c}y^{c}$
, then
$f=x^{a}+y^{b}+x^{c}y^{c}$
, then
![]() $\mathbf{P}=\left\{\mathbf{s}\succcurlyeq 0:\left[\begin{smallmatrix}a & 0 & c\phantom{}\\ 0 & b & c\end{smallmatrix}\right]\mathbf{s}\preccurlyeq \left[\begin{smallmatrix}1\phantom{}\\ 1\end{smallmatrix}\right]\right\}$
is the convex hull of
$\mathbf{P}=\left\{\mathbf{s}\succcurlyeq 0:\left[\begin{smallmatrix}a & 0 & c\phantom{}\\ 0 & b & c\end{smallmatrix}\right]\mathbf{s}\preccurlyeq \left[\begin{smallmatrix}1\phantom{}\\ 1\end{smallmatrix}\right]\right\}$
is the convex hull of
![]() $\mathbf{\text{v}}_{1}=\left(1/a,0,0\right),\mathbf{\text{v}}_{2}=\left(0,1/b,0\right),\mathbf{\text{v}}_{3}=\left(1/a,1/b,0\right)$
,
$\mathbf{\text{v}}_{1}=\left(1/a,0,0\right),\mathbf{\text{v}}_{2}=\left(0,1/b,0\right),\mathbf{\text{v}}_{3}=\left(1/a,1/b,0\right)$
,
![]() $\mathbf{\text{v}}_{4}=\left(0,0,1/c\right)$
, and
$\mathbf{\text{v}}_{4}=\left(0,0,1/c\right)$
, and
![]() $\mathbf{0}$
. The description of
$\mathbf{0}$
. The description of
![]() $\mathbf{P}_{\text{max}}$
depends on the relationship between
$\mathbf{P}_{\text{max}}$
depends on the relationship between
![]() $a,b$
, and
$a,b$
, and
![]() $c$
.
$c$
.
-
(1) If
 $1/a+1/b>1/c$
, then
$1/a+1/b>1/c$
, then
 $\mathbf{P}_{\text{max}}=\{\mathbf{\text{v}}_{3}\}$
.
$\mathbf{P}_{\text{max}}=\{\mathbf{\text{v}}_{3}\}$
. -
(2) If
 $1/a+1/b<1/c$
, then
$1/a+1/b<1/c$
, then
 $\mathbf{P}_{\text{max}}=\{\mathbf{\text{v}}_{4}\}$
.
$\mathbf{P}_{\text{max}}=\{\mathbf{\text{v}}_{4}\}$
. -
(3) If
 $1/a+1/b=1/c$
, then
$1/a+1/b=1/c$
, then
 $\mathbf{P}_{\text{max}}$
is the line segment connecting
$\mathbf{P}_{\text{max}}$
is the line segment connecting
 $\mathbf{\text{v}}_{3}$
and
$\mathbf{\text{v}}_{3}$
and
 $\mathbf{\text{v}}_{4}$
.
$\mathbf{\text{v}}_{4}$
.
Definition 22. We call an element of
![]() $\mathbf{P}_{\text{max}}$
a maximal point, and we say that
$\mathbf{P}_{\text{max}}$
a maximal point, and we say that
![]() $\mathbf{P}$
contains a unique maximal point if
$\mathbf{P}$
contains a unique maximal point if
![]() $^{\#}\mathbf{P}_{\text{max}}=1$
.
$^{\#}\mathbf{P}_{\text{max}}=1$
.
Example 23. In Example 20,
![]() $\mathbf{P}$
always has a unique maximal point. In Example 21, we see that
$\mathbf{P}$
always has a unique maximal point. In Example 21, we see that
![]() $\mathbf{P}$
contains a unique maximal point if and only if
$\mathbf{P}$
contains a unique maximal point if and only if
![]() $1/a+1/b\neq 1/c$
.
$1/a+1/b\neq 1/c$
.
We conclude this discussion by illustrating an important property of polynomials whose splitting polytope contains a unique maximal point. We refer the reader to Remark 34 for a description of this condition in terms of Newton polyhedra.
Lemma 24. Suppose that
![]() $\mathbf{P}$
has a unique maximal point
$\mathbf{P}$
has a unique maximal point
![]() $\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}$
.
$\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}$
.
-
(1) If
 $|\mathbf{s}|=|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|$
and
$|\mathbf{s}|=|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|$
and
 $\mathbf{E}\mathbf{s}=\mathbf{E}\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}$
for some
$\mathbf{E}\mathbf{s}=\mathbf{E}\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}$
for some
 $\mathbf{s}\in \mathbb{R}_{{\geqslant}0}^{n}$
, then
$\mathbf{s}\in \mathbb{R}_{{\geqslant}0}^{n}$
, then
 $\mathbf{s}=\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}$
.
$\mathbf{s}=\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}$
. -
(2) If
 $|\mathbf{s}|=|\boldsymbol{\unicode[STIX]{x1D708}}|,\mathbf{E}\mathbf{s}=\mathbf{E}\boldsymbol{\unicode[STIX]{x1D708}}$
, and
$|\mathbf{s}|=|\boldsymbol{\unicode[STIX]{x1D708}}|,\mathbf{E}\mathbf{s}=\mathbf{E}\boldsymbol{\unicode[STIX]{x1D708}}$
, and
 $\boldsymbol{\unicode[STIX]{x1D708}}\preccurlyeq \langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}$
for some
$\boldsymbol{\unicode[STIX]{x1D708}}\preccurlyeq \langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}$
for some
 $\boldsymbol{\unicode[STIX]{x1D708}},\mathbf{s}$
in
$\boldsymbol{\unicode[STIX]{x1D708}},\mathbf{s}$
in
 $\mathbb{R}_{{\geqslant}0}^{n}$
, then
$\mathbb{R}_{{\geqslant}0}^{n}$
, then
 $\mathbf{s}=\boldsymbol{\unicode[STIX]{x1D708}}$
.
$\mathbf{s}=\boldsymbol{\unicode[STIX]{x1D708}}$
.
Proof. To prove the first statement, let
![]() $\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }:=\mathbf{s}+\boldsymbol{\unicode[STIX]{x1D702}}-\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}$
. By hypothesis,
$\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }:=\mathbf{s}+\boldsymbol{\unicode[STIX]{x1D702}}-\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}$
. By hypothesis,
![]() $\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }\succcurlyeq \mathbf{s}\succcurlyeq \mathbf{0}$
,
$\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }\succcurlyeq \mathbf{s}\succcurlyeq \mathbf{0}$
,
![]() $\mathbf{E}\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }=\mathbf{E}\mathbf{s}+\mathbf{E}\boldsymbol{\unicode[STIX]{x1D702}}-\mathbf{E}\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}=\mathbf{E}\boldsymbol{\unicode[STIX]{x1D702}}$
, and
$\mathbf{E}\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }=\mathbf{E}\mathbf{s}+\mathbf{E}\boldsymbol{\unicode[STIX]{x1D702}}-\mathbf{E}\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}=\mathbf{E}\boldsymbol{\unicode[STIX]{x1D702}}$
, and
![]() $|\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }|=|\mathbf{s}|+|\boldsymbol{\unicode[STIX]{x1D702}}|-|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|=|\boldsymbol{\unicode[STIX]{x1D702}}|$
, which shows that
$|\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }|=|\mathbf{s}|+|\boldsymbol{\unicode[STIX]{x1D702}}|-|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|=|\boldsymbol{\unicode[STIX]{x1D702}}|$
, which shows that
![]() $\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }$
is a maximal point of
$\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }$
is a maximal point of
![]() $\mathbf{P}$
. Thus,
$\mathbf{P}$
. Thus,
![]() $\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }=\boldsymbol{\unicode[STIX]{x1D702}}$
, and
$\boldsymbol{\unicode[STIX]{x1D702}}^{\prime }=\boldsymbol{\unicode[STIX]{x1D702}}$
, and
![]() $\mathbf{s}=\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}$
.
$\mathbf{s}=\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}$
.
For the second statement, let
![]() $\mathbf{s}^{\prime }:=\mathbf{s}+\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}-\boldsymbol{\unicode[STIX]{x1D708}}$
. By hypothesis,
$\mathbf{s}^{\prime }:=\mathbf{s}+\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}-\boldsymbol{\unicode[STIX]{x1D708}}$
. By hypothesis,
![]() $\mathbf{s}^{\prime }\succcurlyeq \mathbf{0}$
,
$\mathbf{s}^{\prime }\succcurlyeq \mathbf{0}$
,
![]() $|\mathbf{s}^{\prime }|=|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|$
, and
$|\mathbf{s}^{\prime }|=|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|$
, and
![]() $\mathbf{E}\mathbf{s}^{\prime }=\mathbf{E}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}$
. The first statement, applied to
$\mathbf{E}\mathbf{s}^{\prime }=\mathbf{E}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}$
. The first statement, applied to
![]() $\mathbf{s}^{\prime }$
, shows that
$\mathbf{s}^{\prime }$
, shows that
![]() $\mathbf{s}^{\prime }=\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}$
, and thus
$\mathbf{s}^{\prime }=\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}$
, and thus
![]() $\mathbf{s}=\boldsymbol{\unicode[STIX]{x1D708}}$
.◻
$\mathbf{s}=\boldsymbol{\unicode[STIX]{x1D708}}$
.◻
Corollary 25. Fix a field
![]() $\mathbb{L}$
of characteristic
$\mathbb{L}$
of characteristic
![]() $p$
, and a polynomial
$p$
, and a polynomial
![]() $f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
in
$f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
in
![]() $\mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin, and such that the associated splitting polytope
$\mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin, and such that the associated splitting polytope
![]() $\mathbf{P}$
has a unique maximal point
$\mathbf{P}$
has a unique maximal point
![]() $\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}$
.
$\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}$
.
-
(1) The coefficient of the monomial
 $x^{p^{e}\mathbf{E}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}}$
in
$x^{p^{e}\mathbf{E}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}}$
in
 $f^{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}$
is
$f^{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}$
is
 $\binom{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}{p^{e}\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}}u^{p^{e}\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}}.$
$\binom{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}{p^{e}\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}}u^{p^{e}\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}}.$
-
(2) If
 $\boldsymbol{\unicode[STIX]{x1D708}}\in \frac{1}{p^{e}}\cdot \mathbb{N}^{n}$
is an index such that
$\boldsymbol{\unicode[STIX]{x1D708}}\in \frac{1}{p^{e}}\cdot \mathbb{N}^{n}$
is an index such that
 $\boldsymbol{\unicode[STIX]{x1D708}}\preccurlyeq \left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}$
, then the coefficient of the monomial
$\boldsymbol{\unicode[STIX]{x1D708}}\preccurlyeq \left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}$
, then the coefficient of the monomial
 $\boldsymbol{x}^{p^{e}\mathbf{E}\boldsymbol{\unicode[STIX]{x1D708}}}$
in
$\boldsymbol{x}^{p^{e}\mathbf{E}\boldsymbol{\unicode[STIX]{x1D708}}}$
in
 $f^{p^{e}|\boldsymbol{\unicode[STIX]{x1D708}}|}$
is
$f^{p^{e}|\boldsymbol{\unicode[STIX]{x1D708}}|}$
is
 $\binom{p^{e}|\boldsymbol{\unicode[STIX]{x1D708}}|}{p^{e}\boldsymbol{\unicode[STIX]{x1D708}}}u^{p^{e}\boldsymbol{\unicode[STIX]{x1D708}}}$
.
$\binom{p^{e}|\boldsymbol{\unicode[STIX]{x1D708}}|}{p^{e}\boldsymbol{\unicode[STIX]{x1D708}}}u^{p^{e}\boldsymbol{\unicode[STIX]{x1D708}}}$
.
Proof. This follows immediately from Lemma 24, and the multinomial theorem. ◻
4.3 Newton polyhedra
Definition 26. Fix an arbitrary field
![]() $\mathbb{L}$
, and consider a polynomial
$\mathbb{L}$
, and consider a polynomial
![]() $f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. We call
$f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. We call
![]() $\mathbf{N}:=\text{convex}(\text{Supp}(f))+\mathbb{R}_{{\geqslant}0}^{m}$
the Newton polyhedron of
$\mathbf{N}:=\text{convex}(\text{Supp}(f))+\mathbb{R}_{{\geqslant}0}^{m}$
the Newton polyhedron of
![]() $f$
.
$f$
.
Remark 27. It follows from the discussion in Section 4.1 that
![]() $\mathbf{N}$
is, indeed, a polyhedron. Moreover, since
$\mathbf{N}$
is, indeed, a polyhedron. Moreover, since
![]() $\text{Supp}(f)\subseteq \mathbb{N}^{m}$
and
$\text{Supp}(f)\subseteq \mathbb{N}^{m}$
and
![]() $\mathbb{R}_{{\geqslant}0}^{m}$
is the cone generated by the standard basis elements of
$\mathbb{R}_{{\geqslant}0}^{m}$
is the cone generated by the standard basis elements of
![]() $\mathbb{Q}^{m}$
, it follows that
$\mathbb{Q}^{m}$
, it follows that
![]() $\mathbf{N}$
is rational.
$\mathbf{N}$
is rational.
Lemma 28. If
![]() $\mathbf{N}$
is the Newton polyhedron of
$\mathbf{N}$
is the Newton polyhedron of
![]() $f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
, then every nonempty face of
$f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
, then every nonempty face of
![]() $\mathbf{N}$
is of the form
$\mathbf{N}$
is of the form
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
, where
$\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
, where
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{Q}_{{\geqslant}0}$
, and
$\unicode[STIX]{x1D6FD}\in \mathbb{Q}_{{\geqslant}0}$
, and
![]() $L\in \mathbb{Q}[z_{1},\ldots ,z_{m}]$
is a
$L\in \mathbb{Q}[z_{1},\ldots ,z_{m}]$
is a
![]() $\mathbb{Q}_{{\geqslant}0}$
-linear combination of the variables. Furthermore, such a face is bounded if and only if
$\mathbb{Q}_{{\geqslant}0}$
-linear combination of the variables. Furthermore, such a face is bounded if and only if
![]() $L$
is a
$L$
is a
![]() $\mathbb{Q}_{{>}0}$
-linear combination of the variables (in which case,
$\mathbb{Q}_{{>}0}$
-linear combination of the variables (in which case,
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{Q}_{{>}0}$
).
$\unicode[STIX]{x1D6FD}\in \mathbb{Q}_{{>}0}$
).
Proof. By Remark 27, every face of
![]() $\mathbf{N}$
is of the form
$\mathbf{N}$
is of the form
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
, where
$\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
, where
![]() $L=\unicode[STIX]{x1D6FD}_{1}z_{1}+\cdots +\unicode[STIX]{x1D6FD}_{m}z_{n}$
, and
$L=\unicode[STIX]{x1D6FD}_{1}z_{1}+\cdots +\unicode[STIX]{x1D6FD}_{m}z_{n}$
, and
![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{m}\in \mathbb{Q}$
. Fix
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{m}\in \mathbb{Q}$
. Fix
![]() $\mathbf{\text{v}}\in \text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
. By definition,
$\mathbf{\text{v}}\in \text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
. By definition,
![]() $\mathbf{\text{v}}+\unicode[STIX]{x1D706}\cdot \mathbf{e}_{i}\in \mathbf{N}$
for every
$\mathbf{\text{v}}+\unicode[STIX]{x1D706}\cdot \mathbf{e}_{i}\in \mathbf{N}$
for every
![]() $\unicode[STIX]{x1D706}>0$
, and so
$\unicode[STIX]{x1D706}>0$
, and so
As
![]() $\unicode[STIX]{x1D706}>0$
, (4.1) implies
$\unicode[STIX]{x1D706}>0$
, (4.1) implies
![]() $\unicode[STIX]{x1D6FD}_{i}\geqslant 0$
. Furthermore, as we have shown that
$\unicode[STIX]{x1D6FD}_{i}\geqslant 0$
. Furthermore, as we have shown that
![]() $L$
is a nonnegative rational combination of the variables, it follows that
$L$
is a nonnegative rational combination of the variables, it follows that
![]() $L\left(\mathbf{N}\right)\subseteq L\left(\mathbb{R}_{{\geqslant}0}^{m}\right)\subseteq \mathbb{R}_{{\geqslant}0}$
. Consequently, as we are assuming that the face
$L\left(\mathbf{N}\right)\subseteq L\left(\mathbb{R}_{{\geqslant}0}^{m}\right)\subseteq \mathbb{R}_{{\geqslant}0}$
. Consequently, as we are assuming that the face
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}=\{\mathbf{\text{v}}\in \mathbf{N}:L(\mathbf{\text{v}})=\unicode[STIX]{x1D6FD}\}$
is nonempty, it follows that
$\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}=\{\mathbf{\text{v}}\in \mathbf{N}:L(\mathbf{\text{v}})=\unicode[STIX]{x1D6FD}\}$
is nonempty, it follows that
![]() $\unicode[STIX]{x1D6FD}$
must be nonnegative. We now prove the second assertion. By Remark 14, we have that
$\unicode[STIX]{x1D6FD}$
must be nonnegative. We now prove the second assertion. By Remark 14, we have that
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
is bounded if and only if for every
$\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
is bounded if and only if for every
![]() $\mathbf{\text{v}}\in \text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
, and nonzero element
$\mathbf{\text{v}}\in \text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
, and nonzero element
![]() $\mathbf{w}\in \mathbb{R}_{{\geqslant}0}^{m}$
, there exists a positive real number
$\mathbf{w}\in \mathbb{R}_{{\geqslant}0}^{m}$
, there exists a positive real number
![]() $\unicode[STIX]{x1D706}$
such that
$\unicode[STIX]{x1D706}$
such that
![]() $\mathbf{\text{v}}+\unicode[STIX]{x1D706}\cdot \mathbf{w}\notin \text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
. Writing
$\mathbf{\text{v}}+\unicode[STIX]{x1D706}\cdot \mathbf{w}\notin \text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
. Writing
![]() $\mathbf{w}=\sum _{i=1}^{m}w_{i}\cdot \mathbf{e}_{i}$
, the preceding condition may be written as
$\mathbf{w}=\sum _{i=1}^{m}w_{i}\cdot \mathbf{e}_{i}$
, the preceding condition may be written as
![]() $\unicode[STIX]{x1D6FD}<L\left(\mathbf{\text{v}}+\unicode[STIX]{x1D706}\cdot \mathbf{w}\right)=L(\mathbf{\text{v}})+\sum _{i=1}^{m}\unicode[STIX]{x1D706}w_{i}\cdot \unicode[STIX]{x1D6FD}_{i}=\unicode[STIX]{x1D6FD}+\sum _{i=1}^{m}\unicode[STIX]{x1D706}w_{i}\cdot \unicode[STIX]{x1D6FD}_{i}$
. As
$\unicode[STIX]{x1D6FD}<L\left(\mathbf{\text{v}}+\unicode[STIX]{x1D706}\cdot \mathbf{w}\right)=L(\mathbf{\text{v}})+\sum _{i=1}^{m}\unicode[STIX]{x1D706}w_{i}\cdot \unicode[STIX]{x1D6FD}_{i}=\unicode[STIX]{x1D6FD}+\sum _{i=1}^{m}\unicode[STIX]{x1D706}w_{i}\cdot \unicode[STIX]{x1D6FD}_{i}$
. As
![]() $\unicode[STIX]{x1D706}>0$
, and as
$\unicode[STIX]{x1D706}>0$
, and as
![]() $\mathbf{w}$
can be chosen arbitrarily, we conclude that
$\mathbf{w}$
can be chosen arbitrarily, we conclude that
![]() $\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
is bounded if and only if
$\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
is bounded if and only if
![]() $\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{m}>0$
. Finally, it follows from the positivity of the coefficients of
$\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{m}>0$
. Finally, it follows from the positivity of the coefficients of
![]() $L$
, along with the fact that every point in
$L$
, along with the fact that every point in
![]() $\mathbf{N}$
is has nonnegative entries (and at least one positive entry), that
$\mathbf{N}$
is has nonnegative entries (and at least one positive entry), that
![]() $L(\mathbf{N})\subseteq \mathbb{R}_{{>}0}$
, and hence that
$L(\mathbf{N})\subseteq \mathbb{R}_{{>}0}$
, and hence that
![]() $\unicode[STIX]{x1D6FD}>0$
.◻
$\unicode[STIX]{x1D6FD}>0$
.◻
Definition 29. By definition, the ray generated by
![]() $\mathbf{1}_{m}$
intersects the boundary of
$\mathbf{1}_{m}$
intersects the boundary of
![]() $\mathbf{N}$
. By [Reference WebsterWeb94, Theorem 3.2.2], this boundary is the union of the exposed faces of
$\mathbf{N}$
. By [Reference WebsterWeb94, Theorem 3.2.2], this boundary is the union of the exposed faces of
![]() $\mathbf{N}$
, and we say that
$\mathbf{N}$
, and we say that
![]() $\mathbf{N}$
is in diagonal position if the ray generated by
$\mathbf{N}$
is in diagonal position if the ray generated by
![]() $\mathbf{1}_{m}$
intersects a bounded face of
$\mathbf{1}_{m}$
intersects a bounded face of
![]() $\mathbf{N}$
.
$\mathbf{N}$
.
4.4 Connections
In this subsection, we fix a field
![]() $\mathbb{L}$
, a polynomial
$\mathbb{L}$
, a polynomial
![]() $f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin, and distinct, nonzero vectors such that
$f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin, and distinct, nonzero vectors such that
![]() $\text{Supp}(f)=\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\}$
.
$\text{Supp}(f)=\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\}$
.
Lemma 31. If
![]() $\mathbf{P}$
and
$\mathbf{P}$
and
![]() $\mathbf{N}$
are the splitting polytope and the Newton polyhedron associated to
$\mathbf{N}$
are the splitting polytope and the Newton polyhedron associated to
![]() $f$
, then
$f$
, then
![]() $\left\{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\smallsetminus \mathbf{0}\right\}=\left\{\unicode[STIX]{x1D706}>0:\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}\in \mathbf{N}\right\}$
. In particular,
$\left\{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\smallsetminus \mathbf{0}\right\}=\left\{\unicode[STIX]{x1D706}>0:\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}\in \mathbf{N}\right\}$
. In particular,
Proof. Fix
![]() $\mathbf{s}\in \mathbf{P}\smallsetminus \mathbf{0}$
. By definition of
$\mathbf{s}\in \mathbf{P}\smallsetminus \mathbf{0}$
. By definition of
![]() $\mathbf{P}$
, we have that
$\mathbf{P}$
, we have that
![]() $\mathbf{E}\mathbf{s}=\sum s_{i}\cdot \mathbf{a}_{i}\preccurlyeq \mathbf{1}_{m}$
, and dividing this through by
$\mathbf{E}\mathbf{s}=\sum s_{i}\cdot \mathbf{a}_{i}\preccurlyeq \mathbf{1}_{m}$
, and dividing this through by
![]() $|\mathbf{s}|\neq 0$
, we see that
$|\mathbf{s}|\neq 0$
, we see that
![]() $\sum \frac{s_{i}}{|\mathbf{s}|}\cdot \mathbf{a}_{i}\preccurlyeq \frac{1}{|\mathbf{s}|}\cdot \mathbf{1}_{m}$
. Consequently, there exists
$\sum \frac{s_{i}}{|\mathbf{s}|}\cdot \mathbf{a}_{i}\preccurlyeq \frac{1}{|\mathbf{s}|}\cdot \mathbf{1}_{m}$
. Consequently, there exists
![]() $\boldsymbol{\unicode[STIX]{x1D6FF}}\in \mathbb{R}^{m}$
with
$\boldsymbol{\unicode[STIX]{x1D6FF}}\in \mathbb{R}^{m}$
with
![]() $\boldsymbol{\unicode[STIX]{x1D6FF}}\succcurlyeq \mathbf{0}$
such that
$\boldsymbol{\unicode[STIX]{x1D6FF}}\succcurlyeq \mathbf{0}$
such that
![]() $\frac{1}{|\mathbf{s}|}\cdot \mathbf{1}_{m}=\sum \frac{s_{i}}{|\mathbf{s}|}\cdot \mathbf{a}_{i}+\boldsymbol{\unicode[STIX]{x1D6FF}}$
, and as
$\frac{1}{|\mathbf{s}|}\cdot \mathbf{1}_{m}=\sum \frac{s_{i}}{|\mathbf{s}|}\cdot \mathbf{a}_{i}+\boldsymbol{\unicode[STIX]{x1D6FF}}$
, and as
![]() $\sum \frac{s_{i}}{|\mathbf{s}|}=1$
, this shows that
$\sum \frac{s_{i}}{|\mathbf{s}|}=1$
, this shows that
![]() $\frac{1}{|\mathbf{s}|}\cdot \mathbf{1}_{m}\in \mathbf{N}$
.
$\frac{1}{|\mathbf{s}|}\cdot \mathbf{1}_{m}\in \mathbf{N}$
.
Next, fix
![]() $\unicode[STIX]{x1D706}\neq 0$
such that
$\unicode[STIX]{x1D706}\neq 0$
such that
![]() $\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}\in \mathbf{N}$
. By definition, there exist nonnegative real numbers
$\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}\in \mathbf{N}$
. By definition, there exist nonnegative real numbers
![]() $\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n}$
with
$\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{n}$
with
![]() $\sum \unicode[STIX]{x1D70E}_{i}=1$
, and a vector
$\sum \unicode[STIX]{x1D70E}_{i}=1$
, and a vector
![]() $\boldsymbol{\unicode[STIX]{x1D6FF}}\succcurlyeq 0$
such that
$\boldsymbol{\unicode[STIX]{x1D6FF}}\succcurlyeq 0$
such that
![]() $\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}=\sum \unicode[STIX]{x1D70E}_{i}\cdot \mathbf{a}_{i}+\boldsymbol{\unicode[STIX]{x1D6FF}}$
, so that
$\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}=\sum \unicode[STIX]{x1D70E}_{i}\cdot \mathbf{a}_{i}+\boldsymbol{\unicode[STIX]{x1D6FF}}$
, so that
![]() $\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}\succcurlyeq \sum \unicode[STIX]{x1D70E}_{i}\cdot \mathbf{a}_{i}$
. Multiplying through by
$\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}\succcurlyeq \sum \unicode[STIX]{x1D70E}_{i}\cdot \mathbf{a}_{i}$
. Multiplying through by
![]() $\unicode[STIX]{x1D706}$
shows that
$\unicode[STIX]{x1D706}$
shows that
![]() $\mathbf{1}_{m}\succcurlyeq \sum \left(\unicode[STIX]{x1D706}\unicode[STIX]{x1D70E}_{i}\right)\cdot \mathbf{a}_{i}$
, and it follows that the vector
$\mathbf{1}_{m}\succcurlyeq \sum \left(\unicode[STIX]{x1D706}\unicode[STIX]{x1D70E}_{i}\right)\cdot \mathbf{a}_{i}$
, and it follows that the vector
![]() $\mathbf{s}:=(\unicode[STIX]{x1D706}\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D706}\unicode[STIX]{x1D70E}_{n})$
is contained in
$\mathbf{s}:=(\unicode[STIX]{x1D706}\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D706}\unicode[STIX]{x1D70E}_{n})$
is contained in
![]() $\mathbf{P}$
, and has coordinate sum
$\mathbf{P}$
, and has coordinate sum
![]() $\unicode[STIX]{x1D706}$
.◻
$\unicode[STIX]{x1D706}$
.◻
Lemma 32. Suppose that
![]() $\mathbf{N}$
is in diagonal position, so that the ray generated by
$\mathbf{N}$
is in diagonal position, so that the ray generated by
![]() $\mathbf{1}_{m}$
intersects some bounded face of
$\mathbf{1}_{m}$
intersects some bounded face of
![]() $\mathbf{N}$
. If
$\mathbf{N}$
. If
![]() $\mathbf{F}$
is such a bounded face of
$\mathbf{F}$
is such a bounded face of
![]() $\mathbf{N}$
, then
$\mathbf{N}$
, then
Proof. By Lemma 28,
![]() $\mathbf{F}=\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
, where
$\mathbf{F}=\text{H}_{\unicode[STIX]{x1D6FD}}^{L}\cap \mathbf{N}$
, where
![]() $\unicode[STIX]{x1D6FD}\in \mathbb{Q}_{{>}0}$
, and
$\unicode[STIX]{x1D6FD}\in \mathbb{Q}_{{>}0}$
, and
![]() $L\in \mathbb{Q}[z_{1},\ldots z_{m}]$
is a positive linear combination of the variables. Moreover, by replacing
$L\in \mathbb{Q}[z_{1},\ldots z_{m}]$
is a positive linear combination of the variables. Moreover, by replacing
![]() $L$
with
$L$
with
![]() $\frac{1}{\unicode[STIX]{x1D6FD}}\cdot L$
, we may, and will, assume that
$\frac{1}{\unicode[STIX]{x1D6FD}}\cdot L$
, we may, and will, assume that
![]() $\unicode[STIX]{x1D6FD}=1$
. Given
$\unicode[STIX]{x1D6FD}=1$
. Given
![]() $\mathbf{s}\in \mathbf{P}_{\text{max}}$
, Lemma 31 implies that
$\mathbf{s}\in \mathbf{P}_{\text{max}}$
, Lemma 31 implies that
![]() $(1/|\mathbf{s}|)\cdot \mathbf{1}_{m}$
, which lies on the ray generated by
$(1/|\mathbf{s}|)\cdot \mathbf{1}_{m}$
, which lies on the ray generated by
![]() $\mathbf{1}_{m}$
, is also contained in the boundary of
$\mathbf{1}_{m}$
, is also contained in the boundary of
![]() $\mathbf{N}$
, and hence lies in
$\mathbf{N}$
, and hence lies in
![]() $\mathbf{F}$
. Consequently,
$\mathbf{F}$
. Consequently,
Restated,
![]() $L(\mathbf{1}_{m})=|\mathbf{s}|$
for every
$L(\mathbf{1}_{m})=|\mathbf{s}|$
for every
![]() $\mathbf{s}\in \mathbf{P}_{\text{max}}$
, which shows that
$\mathbf{s}\in \mathbf{P}_{\text{max}}$
, which shows that
With this observation in hand, we begin our proof. Set
To complete the proof, we must show that
![]() $\mathbf{P}_{\text{max}}=\mathbf{Q}$
. Toward this end, choose
$\mathbf{P}_{\text{max}}=\mathbf{Q}$
. Toward this end, choose
![]() $\mathbf{s}\in \mathbf{P}_{\text{max}}$
. As
$\mathbf{s}\in \mathbf{P}_{\text{max}}$
. As
![]() $L$
has positive coefficients, we may apply it to the bound
$L$
has positive coefficients, we may apply it to the bound
![]() $\mathbf{E}\mathbf{s}\preccurlyeq \mathbf{1}_{m}$
to obtain
$\mathbf{E}\mathbf{s}\preccurlyeq \mathbf{1}_{m}$
to obtain
where we have also used that
![]() $1\leqslant L(\mathbf{a}_{i})$
for all
$1\leqslant L(\mathbf{a}_{i})$
for all
![]() $1\leqslant i\leqslant n$
, by our choice of
$1\leqslant i\leqslant n$
, by our choice of
![]() $L$
. Furthermore, (4.2) shows that all of these inequalities must be, in fact, equalities. If the inequality
$L$
. Furthermore, (4.2) shows that all of these inequalities must be, in fact, equalities. If the inequality
![]() $\mathbf{E}\mathbf{s}\preccurlyeq \mathbf{1}_{m}$
were strict in some component, then the positivity of
$\mathbf{E}\mathbf{s}\preccurlyeq \mathbf{1}_{m}$
were strict in some component, then the positivity of
![]() $L$
would imply that
$L$
would imply that
![]() $L(\mathbf{E}\mathbf{s})<L(\mathbf{1}_{m})$
, which is impossible by our previous observation. On the other hand, if
$L(\mathbf{E}\mathbf{s})<L(\mathbf{1}_{m})$
, which is impossible by our previous observation. On the other hand, if
![]() $s_{k}$
were nonzero (and, hence, positive) for some index
$s_{k}$
were nonzero (and, hence, positive) for some index
![]() $k$
with
$k$
with
![]() $\mathbf{a}_{k}\notin \mathbf{F}$
, then we would have that
$\mathbf{a}_{k}\notin \mathbf{F}$
, then we would have that
![]() $1<L(\mathbf{a}_{k})$
, and, hence, than
$1<L(\mathbf{a}_{k})$
, and, hence, than
![]() $s_{k}<s_{k}\cdot L(\mathbf{a}_{k})$
, which would then force the leftmost inequality above to be strict, which is also impossible. In summary, we have just shown that
$s_{k}<s_{k}\cdot L(\mathbf{a}_{k})$
, which would then force the leftmost inequality above to be strict, which is also impossible. In summary, we have just shown that
![]() $\mathbf{s}\in \mathbf{Q}$
.
$\mathbf{s}\in \mathbf{Q}$
.
Next, fix an element
![]() $\mathbf{s}\in \mathbf{Q}$
, so that
$\mathbf{s}\in \mathbf{Q}$
, so that
![]() $\mathbf{1}_{m}=\mathbf{E}\mathbf{s}=\sum _{\mathbf{a}_{i}\in \mathbf{F}}s_{i}\cdot \mathbf{a}_{i}$
. By our choice of
$\mathbf{1}_{m}=\mathbf{E}\mathbf{s}=\sum _{\mathbf{a}_{i}\in \mathbf{F}}s_{i}\cdot \mathbf{a}_{i}$
. By our choice of
![]() $L$
, we have that
$L$
, we have that
![]() $L(\mathbf{a}_{i})=1$
whenever
$L(\mathbf{a}_{i})=1$
whenever
![]() $\mathbf{a}_{i}\in \mathbf{F}$
, and so applying
$\mathbf{a}_{i}\in \mathbf{F}$
, and so applying
![]() $L$
to this identity shows that
$L$
to this identity shows that
![]() $L(\mathbf{1}_{m})=\sum _{\mathbf{a}_{i}\in \mathbf{F}}s_{i}=|\mathbf{s}|$
, which shows that
$L(\mathbf{1}_{m})=\sum _{\mathbf{a}_{i}\in \mathbf{F}}s_{i}=|\mathbf{s}|$
, which shows that
![]() $\mathbf{s}\in \mathbf{P}_{\text{max}}$
.◻
$\mathbf{s}\in \mathbf{P}_{\text{max}}$
.◻
Remark 33. (Constructing an element of
 $\mathbf{P}_{\text{max}}$
)
$\mathbf{P}_{\text{max}}$
)
It follows immediately from the definition that
![]() $\mathbf{P}_{\text{max}}$
is nonempty. On the other hand, if
$\mathbf{P}_{\text{max}}$
is nonempty. On the other hand, if
![]() $\mathbf{N}$
is in diagonal position, then one may also see this from the description given in the preceding lemma. Suppose
$\mathbf{N}$
is in diagonal position, then one may also see this from the description given in the preceding lemma. Suppose
![]() $\unicode[STIX]{x1D706}>0$
is such that
$\unicode[STIX]{x1D706}>0$
is such that
![]() $(1/\unicode[STIX]{x1D706})\cdot \mathbf{1}_{m}$
lies in a bounded face
$(1/\unicode[STIX]{x1D706})\cdot \mathbf{1}_{m}$
lies in a bounded face
![]() $\mathbf{F}$
of Newton (such a
$\mathbf{F}$
of Newton (such a
![]() $\unicode[STIX]{x1D706}$
exists, by the assumption that
$\unicode[STIX]{x1D706}$
exists, by the assumption that
![]() $\mathbf{N}$
is in diagonal position), then because
$\mathbf{N}$
is in diagonal position), then because
![]() $\mathbf{F}$
is bounded, it is the convex hull of the set
$\mathbf{F}$
is bounded, it is the convex hull of the set
![]() $\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}\cap \mathbf{F}$
, and so we may write both
$\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}\cap \mathbf{F}$
, and so we may write both
![]() $(1/\unicode[STIX]{x1D706})\mathbf{1}_{m}$
and
$(1/\unicode[STIX]{x1D706})\mathbf{1}_{m}$
and
![]() $\mathbf{1}_{m}$
as a nonnegative combination of the elements of
$\mathbf{1}_{m}$
as a nonnegative combination of the elements of
![]() $\left\{\mathbf{a}_{1},\ldots \mathbf{a}_{n}\right\}\cap \mathbf{F}$
. The coefficients in this latter linear combination can be used to produce an element
$\left\{\mathbf{a}_{1},\ldots \mathbf{a}_{n}\right\}\cap \mathbf{F}$
. The coefficients in this latter linear combination can be used to produce an element
![]() $\mathbf{s}$
described in the statement of Lemma 32.
$\mathbf{s}$
described in the statement of Lemma 32.
The condition that
![]() $^{\#}\mathbf{P}_{\text{max}}=1$
appears multiple times in this article, and below we give an alternate description of this condition in terms of the Newton polyhedron
$^{\#}\mathbf{P}_{\text{max}}=1$
appears multiple times in this article, and below we give an alternate description of this condition in terms of the Newton polyhedron
![]() $\mathbf{N}$
whenever
$\mathbf{N}$
whenever
![]() $\mathbf{N}$
is in diagonal position.
$\mathbf{N}$
is in diagonal position.
Remark 34. (A simple characterization of when
 $^{\#}\mathbf{P}_{\text{max}}=1$
)
$^{\#}\mathbf{P}_{\text{max}}=1$
)
Suppose, once more, that
![]() $\mathbf{N}$
is in diagonal position, and let
$\mathbf{N}$
is in diagonal position, and let
![]() $\mathbf{F}$
be the minimal bounded face of
$\mathbf{F}$
be the minimal bounded face of
![]() $\mathbf{N}$
that intersects the ray generated by
$\mathbf{N}$
that intersects the ray generated by
![]() $\mathbf{1}_{m}$
. We claim that
$\mathbf{1}_{m}$
. We claim that
To see why this is the case, first suppose that
![]() $\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}\cap \mathbf{F}$
is a linearly independent set. In this case, if
$\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}\cap \mathbf{F}$
is a linearly independent set. In this case, if
![]() $\mathbf{s}$
and
$\mathbf{s}$
and
![]() $\mathbf{t}$
are in
$\mathbf{t}$
are in
![]() $\mathbf{P}_{\text{max}}$
, then Lemma 32 shows that the
$\mathbf{P}_{\text{max}}$
, then Lemma 32 shows that the
![]() $k$
th entries of
$k$
th entries of
![]() $\mathbf{s}$
and
$\mathbf{s}$
and
![]() $\mathbf{t}$
are zero whenever
$\mathbf{t}$
are zero whenever
![]() $\mathbf{a}_{k}\notin \mathbf{F}$
, and that
$\mathbf{a}_{k}\notin \mathbf{F}$
, and that
The linear independence of these vectors then shows that
![]() $s_{i}=t_{i}$
for every
$s_{i}=t_{i}$
for every
![]() $i$
with
$i$
with
![]() $\mathbf{a}_{i}\in \mathbf{F}$
, and so
$\mathbf{a}_{i}\in \mathbf{F}$
, and so
![]() $\mathbf{s}=\mathbf{t}$
. We conclude that
$\mathbf{s}=\mathbf{t}$
. We conclude that
![]() $^{\#}\mathbf{P}_{\text{max}}=1$
.
$^{\#}\mathbf{P}_{\text{max}}=1$
.
Next, instead suppose that
![]() $\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}\cap \mathbf{F}$
is not a linearly independent set, and fix coefficients so that
$\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}\cap \mathbf{F}$
is not a linearly independent set, and fix coefficients so that
![]() $\sum _{\mathbf{a}_{i}\in \mathbf{F}}\unicode[STIX]{x1D6FF}_{i}\cdot \mathbf{a}_{i}=0$
. As in Remark 33, we may write
$\sum _{\mathbf{a}_{i}\in \mathbf{F}}\unicode[STIX]{x1D6FF}_{i}\cdot \mathbf{a}_{i}=0$
. As in Remark 33, we may write
![]() $\mathbf{1}_{m}$
as a nonnegative rational combination of the vectors in
$\mathbf{1}_{m}$
as a nonnegative rational combination of the vectors in
![]() $\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}\cap \mathbf{F}$
, and the minimality of
$\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}\cap \mathbf{F}$
, and the minimality of
![]() $\mathbf{F}$
guarantees that there exists such a linear combination with positive coefficients. Thus, we may fix positive rational coefficients
$\mathbf{F}$
guarantees that there exists such a linear combination with positive coefficients. Thus, we may fix positive rational coefficients
![]() $\unicode[STIX]{x1D6FE}_{i}$
such that
$\unicode[STIX]{x1D6FE}_{i}$
such that
![]() $\mathbf{1}_{m}=\sum _{\mathbf{a}_{i}\in \mathbf{F}}\unicode[STIX]{x1D6FE}_{i}\cdot \mathbf{a}_{i}$
, and this positivity implies that
$\mathbf{1}_{m}=\sum _{\mathbf{a}_{i}\in \mathbf{F}}\unicode[STIX]{x1D6FE}_{i}\cdot \mathbf{a}_{i}$
, and this positivity implies that
![]() $\unicode[STIX]{x1D6FE}_{i}+\unicode[STIX]{x1D700}\cdot \unicode[STIX]{x1D6FF}_{i}>0$
for every
$\unicode[STIX]{x1D6FE}_{i}+\unicode[STIX]{x1D700}\cdot \unicode[STIX]{x1D6FF}_{i}>0$
for every
![]() $i$
with
$i$
with
![]() $\mathbf{a}_{i}\in \mathbf{F}$
whenever
$\mathbf{a}_{i}\in \mathbf{F}$
whenever
![]() $\unicode[STIX]{x1D700}>0$
is sufficiently small. Fix such an
$\unicode[STIX]{x1D700}>0$
is sufficiently small. Fix such an
![]() $\unicode[STIX]{x1D700}$
, and define an element
$\unicode[STIX]{x1D700}$
, and define an element
![]() $\mathbf{s}\in \mathbb{R}_{{\geqslant}0}^{m}$
as follows:
$\mathbf{s}\in \mathbb{R}_{{\geqslant}0}^{m}$
as follows:
![]() $s_{i}=0$
if
$s_{i}=0$
if
![]() $\mathbf{a}_{i}\notin \mathbf{F}$
, and
$\mathbf{a}_{i}\notin \mathbf{F}$
, and
![]() $s_{i}=\unicode[STIX]{x1D6FE}_{i}+\unicode[STIX]{x1D700}\cdot \unicode[STIX]{x1D6FF}_{i}$
otherwise. It follows that
$s_{i}=\unicode[STIX]{x1D6FE}_{i}+\unicode[STIX]{x1D700}\cdot \unicode[STIX]{x1D6FF}_{i}$
otherwise. It follows that
![]() $s_{i}>0$
if and only if
$s_{i}>0$
if and only if
![]() $\mathbf{a}_{i}\in \mathbf{F}$
, and that
$\mathbf{a}_{i}\in \mathbf{F}$
, and that
This computation and Lemma 32 show that
![]() $\mathbf{s}\in \mathbf{P}_{\text{max}}$
, and as this holds for infinitely many values of
$\mathbf{s}\in \mathbf{P}_{\text{max}}$
, and as this holds for infinitely many values of
![]() $\unicode[STIX]{x1D700}$
, we have that
$\unicode[STIX]{x1D700}$
, we have that
![]() $^{\#}\mathbf{P}_{\text{max}}>1$
.
$^{\#}\mathbf{P}_{\text{max}}>1$
.
Remark 35. (A comparison with another nondegeneracy condition on Newton polyhedra)
Given a face
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $\mathbf{N}$
, let
$\mathbf{N}$
, let
![]() $f_{\unicode[STIX]{x1D70E}}$
denote the polynomial obtained by summing only the terms of
$f_{\unicode[STIX]{x1D70E}}$
denote the polynomial obtained by summing only the terms of
![]() $f$
whose supporting monomials lie in
$f$
whose supporting monomials lie in
![]() $\unicode[STIX]{x1D70E}$
. Recall that
$\unicode[STIX]{x1D70E}$
. Recall that
![]() $f$
is said to be nondegenerate with respect to
$f$
is said to be nondegenerate with respect to
![]() $\mathbf{N}$
whenever the system of equations
$\mathbf{N}$
whenever the system of equations
![]() $\unicode[STIX]{x2202}f_{\unicode[STIX]{x1D70E}}/\unicode[STIX]{x2202}x_{1}=\cdots =\unicode[STIX]{x2202}f_{\unicode[STIX]{x1D70E}}/\unicode[STIX]{x2202}x_{m}=0$
has no solution in
$\unicode[STIX]{x2202}f_{\unicode[STIX]{x1D70E}}/\unicode[STIX]{x2202}x_{1}=\cdots =\unicode[STIX]{x2202}f_{\unicode[STIX]{x1D70E}}/\unicode[STIX]{x2202}x_{m}=0$
has no solution in
![]() $(\mathbb{L}^{\ast })^{m}$
for every face
$(\mathbb{L}^{\ast })^{m}$
for every face
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $\mathbf{N}$
. It is a general principle that polynomials that are nondegenerate with respect to their Newton polyhedra often satisfy certain desirable conditions (for a particularly relevant instance of this, see [Reference HowaldHow01b]).
$\mathbf{N}$
. It is a general principle that polynomials that are nondegenerate with respect to their Newton polyhedra often satisfy certain desirable conditions (for a particularly relevant instance of this, see [Reference HowaldHow01b]).
Note that if
![]() $f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
is a general polynomial of degree
$f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
is a general polynomial of degree
![]() $d$
, then
$d$
, then
![]() $f$
is nondegenerate with respect to
$f$
is nondegenerate with respect to
![]() $\mathbf{N}$
. On the other hand, it is apparent that for such an
$\mathbf{N}$
. On the other hand, it is apparent that for such an
![]() $f$
, the Newton polyhedron
$f$
, the Newton polyhedron
![]() $\mathbf{N}$
is in diagonal position: the ray generated by
$\mathbf{N}$
is in diagonal position: the ray generated by
![]() $\mathbf{1}_{m}$
intersects
$\mathbf{1}_{m}$
intersects
![]() $\mathbf{N}$
in the bounded face
$\mathbf{N}$
in the bounded face
![]() $\unicode[STIX]{x1D70E}=\left\{\mathbf{s}\in \mathbb{R}^{m}:|\mathbf{s}|=d\right\}\cap \mathbf{N}$
of
$\unicode[STIX]{x1D70E}=\left\{\mathbf{s}\in \mathbb{R}^{m}:|\mathbf{s}|=d\right\}\cap \mathbf{N}$
of
![]() $\mathbf{N}$
. According to Remark 34, we then have that
$\mathbf{N}$
. According to Remark 34, we then have that
![]() $^{\#}\mathbf{P}_{\text{max}}=1$
if and only if the supporting monomials of
$^{\#}\mathbf{P}_{\text{max}}=1$
if and only if the supporting monomials of
![]() $f$
lying on this face are linearly independent, which is impossible for dimension reasons. Thus,
$f$
lying on this face are linearly independent, which is impossible for dimension reasons. Thus,
![]() $^{\#}\mathbf{P}_{\text{max}}>1$
.
$^{\#}\mathbf{P}_{\text{max}}>1$
.
As illustrated by this example, the condition that
![]() $f$
be nondegenerate with respect to
$f$
be nondegenerate with respect to
![]() $\mathbf{N}$
can be quite different from the condition that
$\mathbf{N}$
can be quite different from the condition that
![]() $^{\#}\mathbf{P}_{\text{max}}=1$
. Indeed, as seen above, the latter condition may depend on the coefficients in
$^{\#}\mathbf{P}_{\text{max}}=1$
. Indeed, as seen above, the latter condition may depend on the coefficients in
![]() $f$
, while the former only depends on the supporting monomials of
$f$
, while the former only depends on the supporting monomials of
![]() $f$
.
$f$
.
5 Polyhedra and
 $F$
-pure thresholds
$F$
-pure thresholds
Proposition 36. Fix a field
![]() $\mathbb{L}$
of characteristic
$\mathbb{L}$
of characteristic
![]() $p>0$
, and consider a polynomial
$p>0$
, and consider a polynomial
![]() $f$
in
$f$
in
![]() $\mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. If
$\mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. If
![]() $\mathbf{P}$
is the splitting polytope associated to
$\mathbf{P}$
is the splitting polytope associated to
![]() $f$
, and
$f$
, and
![]() $\mathfrak{a}_{f}$
is the term ideal of
$\mathfrak{a}_{f}$
is the term ideal of
![]() $f$
, then
$f$
, then
![]() $\mathbf{fpt}(\mathfrak{a}_{f})=\max \left\{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\right\}=\max \left\{\unicode[STIX]{x1D706}\neq 0:\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}\in \mathbf{N}\right\}$
.
$\mathbf{fpt}(\mathfrak{a}_{f})=\max \left\{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\right\}=\max \left\{\unicode[STIX]{x1D706}\neq 0:\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}\in \mathbf{N}\right\}$
.
Proof. Fix distinct, nonzero vectors in
![]() $\mathbb{N}^{m}$
such that
$\mathbb{N}^{m}$
such that
![]() $\text{Supp}(f)=\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}$
. By Lemma 31, it suffices to establish the first equality. By definition,
$\text{Supp}(f)=\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}$
. By Lemma 31, it suffices to establish the first equality. By definition,
![]() $\mathfrak{a}:=\mathfrak{a}_{f}=(x^{\mathbf{a}_{1}},\ldots ,x^{\mathbf{a}_{n}})$
, and hence the ideal
$\mathfrak{a}:=\mathfrak{a}_{f}=(x^{\mathbf{a}_{1}},\ldots ,x^{\mathbf{a}_{n}})$
, and hence the ideal
![]() $\mathfrak{a}^{N}$
is generated by monomials of the form
$\mathfrak{a}^{N}$
is generated by monomials of the form
![]() $x^{k_{1}\mathbf{a}_{1}+\cdots +k_{n}\mathbf{a}_{n}}=x^{\mathbf{E}\mathbf{k}}$
with
$x^{k_{1}\mathbf{a}_{1}+\cdots +k_{n}\mathbf{a}_{n}}=x^{\mathbf{E}\mathbf{k}}$
with
![]() $|\mathbf{k}|=k_{1}+\cdots +k_{n}=N$
. As
$|\mathbf{k}|=k_{1}+\cdots +k_{n}=N$
. As
![]() $\mathfrak{a}^{\unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)}\notin \mathfrak{m}^{[p^{e}]}$
, there exists
$\mathfrak{a}^{\unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)}\notin \mathfrak{m}^{[p^{e}]}$
, there exists
![]() $\mathbf{k}\in \mathbb{N}^{n}$
with
$\mathbf{k}\in \mathbb{N}^{n}$
with
![]() $|\mathbf{k}|=\unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)$
such that
$|\mathbf{k}|=\unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)$
such that
![]() $\boldsymbol{x}^{\mathbf{E}\mathbf{k}}\notin \mathfrak{m}^{[p^{e}]}$
. By definition,
$\boldsymbol{x}^{\mathbf{E}\mathbf{k}}\notin \mathfrak{m}^{[p^{e}]}$
. By definition,
![]() $p^{-e}\cdot \mathbf{k}\in \mathbf{P}$
, and consequently
$p^{-e}\cdot \mathbf{k}\in \mathbf{P}$
, and consequently
![]() $p^{-e}\cdot \unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)=p^{-e}\cdot |\mathbf{k}|=\left|p^{-e}\cdot \mathbf{k}\right|$
, which by definition is bounded above by
$p^{-e}\cdot \unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)=p^{-e}\cdot |\mathbf{k}|=\left|p^{-e}\cdot \mathbf{k}\right|$
, which by definition is bounded above by
![]() $\max \left\{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\right\}$
. Taking
$\max \left\{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\right\}$
. Taking
![]() $e\rightarrow \infty$
then shows that
$e\rightarrow \infty$
then shows that
![]() $\mathbf{fpt}(\mathfrak{a})\leqslant \max \left\{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\right\}$
. Next, choose
$\mathbf{fpt}(\mathfrak{a})\leqslant \max \left\{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\right\}$
. Next, choose
![]() $\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
. As
$\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
. As
![]() $\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}\prec \boldsymbol{\unicode[STIX]{x1D702}}$
, we have that
$\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}\prec \boldsymbol{\unicode[STIX]{x1D702}}$
, we have that
![]() $\mathbf{E}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}\prec \mathbf{E}\boldsymbol{\unicode[STIX]{x1D702}}\preccurlyeq \text{}\text{1}_{m}$
, and so
$\mathbf{E}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}\prec \mathbf{E}\boldsymbol{\unicode[STIX]{x1D702}}\preccurlyeq \text{}\text{1}_{m}$
, and so
![]() $x^{p^{e}\mathbf{E}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}}$
is contained in
$x^{p^{e}\mathbf{E}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}}$
is contained in
![]() $\mathfrak{a}^{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}$
but not
$\mathfrak{a}^{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}$
but not
![]() $\mathfrak{m}^{[p^{e}]}$
. It follows that
$\mathfrak{m}^{[p^{e}]}$
. It follows that
![]() $p^{-e}\cdot \unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)\geqslant |\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|$
, and letting
$p^{-e}\cdot \unicode[STIX]{x1D708}_{\mathfrak{a}}\left(p^{e}\right)\geqslant |\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|$
, and letting
![]() $e\rightarrow \infty$
shows that
$e\rightarrow \infty$
shows that
![]() $\mathbf{fpt}(\mathfrak{a})\geqslant |\boldsymbol{\unicode[STIX]{x1D702}}|=\max \{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\}$
.◻
$\mathbf{fpt}(\mathfrak{a})\geqslant |\boldsymbol{\unicode[STIX]{x1D702}}|=\max \{|\mathbf{s}|:\mathbf{s}\in \mathbf{P}\}$
.◻
Corollary 37. If
![]() $\mathbb{L}$
is a field of characteristic
$\mathbb{L}$
is a field of characteristic
![]() $p>0$
, and
$p>0$
, and
![]() $f$
in
$f$
in
![]() $\mathbb{L}[x_{1},\ldots ,x_{m}]$
is a polynomial vanishing at the origin, then the following are equivalent.
$\mathbb{L}[x_{1},\ldots ,x_{m}]$
is a polynomial vanishing at the origin, then the following are equivalent.
-
(1) There exists a maximal point
 $\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
with
$\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
with
 $(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
.
$(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
. -
(2)
 $(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a}_{f})\in \mathbb{N}$
and
$(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a}_{f})\in \mathbb{N}$
and
 $\mathfrak{a}_{f}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a}_{f})}\notin \mathfrak{m}^{[p^{e}]}$
.
$\mathfrak{a}_{f}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a}_{f})}\notin \mathfrak{m}^{[p^{e}]}$
.
Furthermore, if either condition holds and
![]() $\mathbf{N}$
is in diagonal position, then
$\mathbf{N}$
is in diagonal position, then
Proof. Set
![]() $\text{Supp}(f)=\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}$
, and
$\text{Supp}(f)=\left\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}\right\}$
, and
![]() $\mathfrak{a}=\mathfrak{a}_{f}$
. By definition,
$\mathfrak{a}=\mathfrak{a}_{f}$
. By definition,
![]() $\mathfrak{a}^{N}$
is generated by the monomials
$\mathfrak{a}^{N}$
is generated by the monomials
![]() $\boldsymbol{x}^{\mathbf{E}\mathbf{k}}$
with
$\boldsymbol{x}^{\mathbf{E}\mathbf{k}}$
with
![]() $|\mathbf{k}|=N$
. If
$|\mathbf{k}|=N$
. If
![]() $\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
and
$\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
and
![]() $(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
, then it follows from Proposition 36 that
$(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
, then it follows from Proposition 36 that
![]() $(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})=(p^{e}-1)\cdot |\boldsymbol{\unicode[STIX]{x1D702}}|\in \mathbb{N}$
, and since
$(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})=(p^{e}-1)\cdot |\boldsymbol{\unicode[STIX]{x1D702}}|\in \mathbb{N}$
, and since
![]() $\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
, we have that
$\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
, we have that
![]() $x^{(p^{e}-1)\cdot \mathbf{E}\boldsymbol{\unicode[STIX]{x1D702}}}$
is in
$x^{(p^{e}-1)\cdot \mathbf{E}\boldsymbol{\unicode[STIX]{x1D702}}}$
is in
![]() $\mathfrak{a}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}$
, but not in
$\mathfrak{a}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}$
, but not in
![]() $\mathfrak{m}^{[p^{e}]}$
. Conversely, if
$\mathfrak{m}^{[p^{e}]}$
. Conversely, if
![]() $(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})\in \mathbb{N}$
, and
$(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})\in \mathbb{N}$
, and
![]() $\mathfrak{a}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}\not \subseteq \mathfrak{m}^{[p^{e}]}$
, there exists
$\mathfrak{a}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}\not \subseteq \mathfrak{m}^{[p^{e}]}$
, there exists
![]() $\mathbf{k}\in \mathbb{N}^{n}$
such that
$\mathbf{k}\in \mathbb{N}^{n}$
such that
![]() $|\mathbf{k}|=(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})$
and
$|\mathbf{k}|=(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})$
and
![]() $\boldsymbol{x}^{\mathbf{E}\mathbf{k}}\notin \mathfrak{m}^{[p^{e}]}$
, so that
$\boldsymbol{x}^{\mathbf{E}\mathbf{k}}\notin \mathfrak{m}^{[p^{e}]}$
, so that
![]() $\frac{1}{p^{e}-1}\cdot \mathbf{k}\in \mathbf{P}_{\text{max}}$
. Having proven the equivalence, it remains to establish the last assertion, which we do now. We have just seen that the monomials in
$\frac{1}{p^{e}-1}\cdot \mathbf{k}\in \mathbf{P}_{\text{max}}$
. Having proven the equivalence, it remains to establish the last assertion, which we do now. We have just seen that the monomials in
![]() $\mathfrak{a}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}$
not contained in
$\mathfrak{a}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}$
not contained in
![]() $\mathfrak{m}^{[p^{e}]}$
are of the form
$\mathfrak{m}^{[p^{e}]}$
are of the form
![]() $\boldsymbol{x}^{\mathbf{E}\mathbf{k}}$
for some index
$\boldsymbol{x}^{\mathbf{E}\mathbf{k}}$
for some index
![]() $\mathbf{k}$
satisfying
$\mathbf{k}$
satisfying
![]() $\frac{1}{p^{e}-1}\cdot \mathbf{k}\in \mathbf{P}_{\text{max}}$
. By Lemma 32,
$\frac{1}{p^{e}-1}\cdot \mathbf{k}\in \mathbf{P}_{\text{max}}$
. By Lemma 32,
![]() $\mathbf{E}\mathbf{k}=(p^{e}-1)\cdot \mathbf{1}_{m}$
, and it follows that the only monomial in
$\mathbf{E}\mathbf{k}=(p^{e}-1)\cdot \mathbf{1}_{m}$
, and it follows that the only monomial in
![]() $\mathfrak{a}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}$
not in
$\mathfrak{a}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}$
not in
![]() $\mathfrak{m}^{[p^{e}]}$
is
$\mathfrak{m}^{[p^{e}]}$
is
![]() $x^{(p^{e}-1)\cdot \mathbf{1}_{m}}$
.◻
$x^{(p^{e}-1)\cdot \mathbf{1}_{m}}$
.◻
Proposition 38. Fix a field
![]() $\mathbb{L}$
of characteristic
$\mathbb{L}$
of characteristic
![]() $p$
, and a polynomial
$p$
, and a polynomial
![]() $f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. We fix distinct, nonzero vectors
$f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. We fix distinct, nonzero vectors
![]() $\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}$
in
$\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}$
in
![]() $\mathbb{N}^{m}$
, and nonzero elements
$\mathbb{N}^{m}$
, and nonzero elements
![]() $u_{1},\ldots ,u_{n}$
in
$u_{1},\ldots ,u_{n}$
in
![]() $\mathbb{L}$
, so that
$\mathbb{L}$
, so that
![]() $f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
. If
$f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
. If
![]() $\mathbf{N}$
is in diagonal position, and if
$\mathbf{N}$
is in diagonal position, and if
![]() $(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
for some
$(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
for some
![]() $\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
and
$\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
and
![]() $e\geqslant 1$
, then there exists a nonzero polynomial
$e\geqslant 1$
, then there exists a nonzero polynomial
![]() $\unicode[STIX]{x1D6E9}\in \mathbb{Z}[w_{1},\ldots ,w_{n}]$
satisfying the following conditions.
$\unicode[STIX]{x1D6E9}\in \mathbb{Z}[w_{1},\ldots ,w_{n}]$
satisfying the following conditions.
-
(1)
 $f^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a}_{f})}\equiv \unicode[STIX]{x1D6E9}(u_{1},\ldots ,u_{r})\cdot x_{1}^{p^{e}-1}\cdots x_{m}^{p^{e}-1}\hspace{0.2em}\bmod \hspace{0.2em}\mathfrak{m}^{[p^{e}]}$
.
$f^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a}_{f})}\equiv \unicode[STIX]{x1D6E9}(u_{1},\ldots ,u_{r})\cdot x_{1}^{p^{e}-1}\cdots x_{m}^{p^{e}-1}\hspace{0.2em}\bmod \hspace{0.2em}\mathfrak{m}^{[p^{e}]}$
. -
(2) If
 $e=1$
and
$e=1$
and
 $\mathbf{fpt}(\mathfrak{a}_{f})\leqslant 1$
, then
$\mathbf{fpt}(\mathfrak{a}_{f})\leqslant 1$
, then
 $\unicode[STIX]{x1D6E9}$
has nonzero image in
$\unicode[STIX]{x1D6E9}$
has nonzero image in
 $\mathbb{F}_{p}[w_{1},\ldots ,w_{n}]$
.
$\mathbb{F}_{p}[w_{1},\ldots ,w_{n}]$
.
Proof. Set
![]() $\mathfrak{a}=\mathfrak{a}_{f}$
. By definition,
$\mathfrak{a}=\mathfrak{a}_{f}$
. By definition,
![]() $f^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}\in \mathfrak{a}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}$
, and Corollary 37 then implies that
$f^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}\in \mathfrak{a}^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}$
, and Corollary 37 then implies that
![]() $f^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}$
is a multiple of
$f^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}$
is a multiple of
![]() $x^{(p^{e}-1)\cdot \mathbf{1}_{m}}$
modulo
$x^{(p^{e}-1)\cdot \mathbf{1}_{m}}$
modulo
![]() $\mathfrak{m}^{[p^{e}]}$
. Moreover, the multinomial theorem identifies this multiple as
$\mathfrak{m}^{[p^{e}]}$
. Moreover, the multinomial theorem identifies this multiple as
![]() $\unicode[STIX]{x1D6E9}(u_{1},\ldots ,u_{r})\cdot x^{(p^{e}-1)\cdot \mathbf{1}_{m}}$
mod
$\unicode[STIX]{x1D6E9}(u_{1},\ldots ,u_{r})\cdot x^{(p^{e}-1)\cdot \mathbf{1}_{m}}$
mod
![]() $\mathfrak{m}^{[p^{e}]}$
, where
$\mathfrak{m}^{[p^{e}]}$
, where
and the sum in (5.1) extends over all
![]() $\mathbf{k}=(k_{1},\ldots ,k_{n})\in \mathbb{N}^{n}$
such that
$\mathbf{k}=(k_{1},\ldots ,k_{n})\in \mathbb{N}^{n}$
such that
![]() $|\mathbf{k}|=(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})$
. (Note that, for such an index, we have that
$|\mathbf{k}|=(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})$
. (Note that, for such an index, we have that
![]() $\frac{1}{p^{e}-1}\cdot \mathbf{k}$
is in
$\frac{1}{p^{e}-1}\cdot \mathbf{k}$
is in
![]() $\mathbf{P}_{\text{max}}$
, and, hence, Lemma 32 implies that
$\mathbf{P}_{\text{max}}$
, and, hence, Lemma 32 implies that
![]() $\mathbf{E}\mathbf{k}=(p^{e}-1)\cdot \mathbf{1}_{m}$
, making this condition redundant.) By assumption, there exists
$\mathbf{E}\mathbf{k}=(p^{e}-1)\cdot \mathbf{1}_{m}$
, making this condition redundant.) By assumption, there exists
![]() $\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
with
$\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
with
![]() $(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
; as this index corresponds to a nonzero summand in (5.1), we conclude that
$(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
; as this index corresponds to a nonzero summand in (5.1), we conclude that
![]() $\unicode[STIX]{x1D6E9}$
is a nonzero polynomial over
$\unicode[STIX]{x1D6E9}$
is a nonzero polynomial over
![]() $\mathbb{Z}$
. For the last point, note that if
$\mathbb{Z}$
. For the last point, note that if
![]() $\mathbf{fpt}(\mathfrak{a})\leqslant 1$
, then
$\mathbf{fpt}(\mathfrak{a})\leqslant 1$
, then
![]() $(p-1)\cdot \mathbf{fpt}(\mathfrak{a})\leqslant p-1$
, and hence the multinomial coefficients in (5.1) are nonzero modulo
$(p-1)\cdot \mathbf{fpt}(\mathfrak{a})\leqslant p-1$
, and hence the multinomial coefficients in (5.1) are nonzero modulo
![]() $p$
.◻
$p$
.◻
Corollary 39. Fix a field
![]() $\mathbb{L}$
of characteristic
$\mathbb{L}$
of characteristic
![]() $p$
, and a polynomial
$p$
, and a polynomial
![]() $f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. We fix distinct, nonzero vectors
$f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. We fix distinct, nonzero vectors
![]() $\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}$
in
$\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}$
in
![]() $\mathbb{N}^{m}$
, and nonzero elements
$\mathbb{N}^{m}$
, and nonzero elements
![]() $u_{1},\ldots ,u_{n}$
in
$u_{1},\ldots ,u_{n}$
in
![]() $\mathbb{L}$
, so that
$\mathbb{L}$
, so that
![]() $f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
. If
$f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
. If
![]() $\mathbf{N}$
is in diagonal position, and if
$\mathbf{N}$
is in diagonal position, and if
![]() $\mathbf{P}$
contains a unique maximal point
$\mathbf{P}$
contains a unique maximal point
![]() $\boldsymbol{\unicode[STIX]{x1D702}}$
such that
$\boldsymbol{\unicode[STIX]{x1D702}}$
such that
![]() $(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
for some
$(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
for some
![]() $e\geqslant 1$
, then
$e\geqslant 1$
, then
Proof. As
![]() $\mathbf{P}_{\text{max}}=\left\{\boldsymbol{\unicode[STIX]{x1D702}}\right\}$
, (5.1) implies that the only summand appearing in
$\mathbf{P}_{\text{max}}=\left\{\boldsymbol{\unicode[STIX]{x1D702}}\right\}$
, (5.1) implies that the only summand appearing in
![]() $\unicode[STIX]{x1D6E9}$
corresponds to
$\unicode[STIX]{x1D6E9}$
corresponds to
![]() $\mathbf{k}=(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}$
, and the claim then follows from Proposition 38.◻
$\mathbf{k}=(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}$
, and the claim then follows from Proposition 38.◻
Proposition 40. Fix a field
![]() $\mathbb{L}$
of characteristic
$\mathbb{L}$
of characteristic
![]() $p$
, and a polynomial
$p$
, and a polynomial
![]() $f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. We fix distinct, nonzero vectors
$f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. We fix distinct, nonzero vectors
![]() $\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}$
in
$\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}$
in
![]() $\mathbb{N}^{m}$
, and nonzero elements
$\mathbb{N}^{m}$
, and nonzero elements
![]() $u_{1},\ldots ,u_{n}$
in
$u_{1},\ldots ,u_{n}$
in
![]() $\mathbb{L}$
, so that
$\mathbb{L}$
, so that
![]() $f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
. If
$f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
. If
![]() $\mathbf{fpt}(\mathfrak{a}_{f})\leqslant 1$
,
$\mathbf{fpt}(\mathfrak{a}_{f})\leqslant 1$
,
![]() $\mathbf{N}$
is in diagonal position, and
$\mathbf{N}$
is in diagonal position, and
![]() $(p-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
for some
$(p-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
for some
![]() $\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
, then there exists a nonempty closed set
$\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}$
, then there exists a nonempty closed set
![]() $Z\subseteq \mathbb{A}_{\mathbb{L}}^{n}$
such that
$Z\subseteq \mathbb{A}_{\mathbb{L}}^{n}$
such that
![]() $\mathbf{fpt}(f)=\mathbf{fpt}(\mathfrak{a}_{f})$
whenever
$\mathbf{fpt}(f)=\mathbf{fpt}(\mathfrak{a}_{f})$
whenever
![]() $(u_{1},\ldots ,u_{n})\notin Z$
.
$(u_{1},\ldots ,u_{n})\notin Z$
.
Proof. Let
![]() $\unicode[STIX]{x1D6E9}\in \mathbb{Z}[w_{1},\ldots ,w_{n}]$
be as in Proposition 38. The assumption that
$\unicode[STIX]{x1D6E9}\in \mathbb{Z}[w_{1},\ldots ,w_{n}]$
be as in Proposition 38. The assumption that
![]() $\mathbf{fpt}(\mathfrak{a}_{f})\leqslant 1$
implies that
$\mathbf{fpt}(\mathfrak{a}_{f})\leqslant 1$
implies that
![]() $\unicode[STIX]{x1D6E9}$
is nonzero modulo
$\unicode[STIX]{x1D6E9}$
is nonzero modulo
![]() $p$
, and hence defines a nonempty closed set
$p$
, and hence defines a nonempty closed set
![]() $Z$
in
$Z$
in
![]() $\mathbb{A}_{\mathbb{L}}^{n}$
. Moreover, Proposition 38 shows that, if
$\mathbb{A}_{\mathbb{L}}^{n}$
. Moreover, Proposition 38 shows that, if
![]() $(u_{1},\ldots ,u_{n})\notin Z$
, then
$(u_{1},\ldots ,u_{n})\notin Z$
, then
![]() $f^{(p-1)\cdot \mathbf{fpt}(\mathfrak{a}_{f})}\notin \mathfrak{m}^{[p^{}]}$
, and Lemma 13 then shows that
$f^{(p-1)\cdot \mathbf{fpt}(\mathfrak{a}_{f})}\notin \mathfrak{m}^{[p^{}]}$
, and Lemma 13 then shows that
![]() $\mathbf{fpt}(f)\geqslant \mathbf{fpt}(\mathfrak{a}_{f})$
. As the opposite inequality always holds, we conclude that
$\mathbf{fpt}(f)\geqslant \mathbf{fpt}(\mathfrak{a}_{f})$
. As the opposite inequality always holds, we conclude that
![]() $\mathbf{fpt}(f)=\mathbf{fpt}(\mathfrak{a}_{f})$
whenever
$\mathbf{fpt}(f)=\mathbf{fpt}(\mathfrak{a}_{f})$
whenever
![]() $(u_{1},\ldots ,u_{n})\notin Z$
.◻
$(u_{1},\ldots ,u_{n})\notin Z$
.◻
Remark 41. The condition that
![]() $(p-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
in Proposition 40 is necessary. Indeed, if
$(p-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}^{n}$
in Proposition 40 is necessary. Indeed, if
![]() $f=u_{1}x_{d}^{d}+\cdots +u_{d}x_{d}^{d}$
is a degree
$f=u_{1}x_{d}^{d}+\cdots +u_{d}x_{d}^{d}$
is a degree
![]() $d$
Fermat hypersurface, we have seen in Example 20 that
$d$
Fermat hypersurface, we have seen in Example 20 that
![]() $\boldsymbol{\unicode[STIX]{x1D702}}=\left(\frac{1}{d},\ldots ,\frac{1}{d}\right)$
is the unique maximal point of
$\boldsymbol{\unicode[STIX]{x1D702}}=\left(\frac{1}{d},\ldots ,\frac{1}{d}\right)$
is the unique maximal point of
![]() $\mathbf{P}$
, so that
$\mathbf{P}$
, so that
![]() $\mathbf{fpt}(\mathfrak{a}_{f})=\frac{1}{d}+\cdots +\frac{1}{d}=1$
by Proposition 36. However, it is shown in [Reference HernándezHer15] that, if
$\mathbf{fpt}(\mathfrak{a}_{f})=\frac{1}{d}+\cdots +\frac{1}{d}=1$
by Proposition 36. However, it is shown in [Reference HernándezHer15] that, if
![]() $(p-1)\cdot \frac{1}{d}\notin \mathbb{N}$
, then
$(p-1)\cdot \frac{1}{d}\notin \mathbb{N}$
, then
![]() $\mathbf{fpt}(f)<\mathbf{fpt}(\mathfrak{a}_{f})$
for every choice of coefficients
$\mathbf{fpt}(f)<\mathbf{fpt}(\mathfrak{a}_{f})$
for every choice of coefficients
![]() $(u_{1},\ldots ,u_{n})$
.
$(u_{1},\ldots ,u_{n})$
.
Theorem 42. Fix a field
![]() $\mathbb{L}$
of characteristic
$\mathbb{L}$
of characteristic
![]() $p$
, and a polynomial
$p$
, and a polynomial
![]() $f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. Suppose that the associated splitting polytope
$f\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
vanishing at the origin. Suppose that the associated splitting polytope
![]() $\mathbf{P}$
contains a unique maximal point
$\mathbf{P}$
contains a unique maximal point
![]() $\boldsymbol{\unicode[STIX]{x1D702}}$
, and let
$\boldsymbol{\unicode[STIX]{x1D702}}$
, and let
![]() $L=\inf \left\{e\geqslant 0:{\unicode[STIX]{x1D702}_{1}}^{(e+1)}+\cdots +{\unicode[STIX]{x1D702}_{n}}^{(e+1)}\geqslant p\right\}$
, where
$L=\inf \left\{e\geqslant 0:{\unicode[STIX]{x1D702}_{1}}^{(e+1)}+\cdots +{\unicode[STIX]{x1D702}_{n}}^{(e+1)}\geqslant p\right\}$
, where
![]() ${\unicode[STIX]{x1D702}_{i}}^{(e)}$
is the
${\unicode[STIX]{x1D702}_{i}}^{(e)}$
is the
![]() $e$
th digit of
$e$
th digit of
![]() $\unicode[STIX]{x1D702}_{i}$
.
$\unicode[STIX]{x1D702}_{i}$
.
-
(1) If
 $L=\infty$
, then
$L=\infty$
, then
 $\mathbf{fpt}(f)=\mathbf{fpt}(\mathfrak{a}_{f})$
. The converse holds if
$\mathbf{fpt}(f)=\mathbf{fpt}(\mathfrak{a}_{f})$
. The converse holds if
 $\mathbf{N}$
is in diagonal position and
$\mathbf{N}$
is in diagonal position and
 $p$
does not divide any of the denominators of
$p$
does not divide any of the denominators of
 $\boldsymbol{\unicode[STIX]{x1D702}}$
.
$\boldsymbol{\unicode[STIX]{x1D702}}$
. -
(2) If
 $L<\infty$
, then
$L<\infty$
, then
 $\mathbf{fpt}(f)\geqslant \left\langle \unicode[STIX]{x1D702}_{1}\right\rangle _{L}+\cdots +\left\langle \unicode[STIX]{x1D702}_{n}\right\rangle _{L}+\frac{1}{p^{L}}$
.
$\mathbf{fpt}(f)\geqslant \left\langle \unicode[STIX]{x1D702}_{1}\right\rangle _{L}+\cdots +\left\langle \unicode[STIX]{x1D702}_{n}\right\rangle _{L}+\frac{1}{p^{L}}$
.
Proof. We fix distinct, nonzero vectors
![]() $\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}$
in
$\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}$
in
![]() $\mathbb{N}^{m}$
, and nonzero elements
$\mathbb{N}^{m}$
, and nonzero elements
![]() $u_{1},\ldots ,u_{n}$
in
$u_{1},\ldots ,u_{n}$
in
![]() $\mathbb{L}$
, so that
$\mathbb{L}$
, so that
![]() $f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
. We first prove (1), and thus assume that
$f=\sum _{i=1}^{n}u_{i}\cdot x^{\mathbf{a}_{i}}$
. We first prove (1), and thus assume that
![]() $L=\infty$
(i.e., that entries of
$L=\infty$
(i.e., that entries of
![]() $\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying). Corollary 25 gives that, after gathering terms,
$\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying). Corollary 25 gives that, after gathering terms,
appears as a summand of
![]() $f^{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}$
. By definition, each
$f^{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}$
. By definition, each
![]() $u_{i}\in \mathbb{L}^{\ast }$
, so
$u_{i}\in \mathbb{L}^{\ast }$
, so
![]() $u^{p^{e}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}}\neq 0$
. Moreover, as the entries of
$u^{p^{e}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}}\neq 0$
. Moreover, as the entries of
![]() $\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying, it follows from Corollary 7 that
$\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying, it follows from Corollary 7 that
![]() $\binom{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}{p^{e}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}}\neq 0~\text{mod}~p$
for every
$\binom{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}{p^{e}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}}\neq 0~\text{mod}~p$
for every
![]() $e\geqslant 1$
. Finally,
$e\geqslant 1$
. Finally,
![]() $\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}\preccurlyeq \boldsymbol{\unicode[STIX]{x1D702}}$
, and so every entry of
$\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}\preccurlyeq \boldsymbol{\unicode[STIX]{x1D702}}$
, and so every entry of
![]() $p^{e}\mathbf{E}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}$
is less than or equal to
$p^{e}\mathbf{E}\left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}$
is less than or equal to
![]() $p^{e}-1$
. We see then that the monomial in (5.2) is in
$p^{e}-1$
. We see then that the monomial in (5.2) is in
![]() $\text{Supp}\left(f^{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}\right)$
, but not in
$\text{Supp}\left(f^{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}\right)$
, but not in
![]() $\mathfrak{m}^{[p^{e}]}$
. Thus,
$\mathfrak{m}^{[p^{e}]}$
. Thus,
![]() $f^{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}\notin \mathfrak{m}^{[p^{e}]}$
, and so
$f^{p^{e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|}\notin \mathfrak{m}^{[p^{e}]}$
, and so
![]() $\frac{\unicode[STIX]{x1D708}_{f}\left(p^{e}\right)}{p^{e}}\geqslant |\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|$
. Letting
$\frac{\unicode[STIX]{x1D708}_{f}\left(p^{e}\right)}{p^{e}}\geqslant |\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{e}|$
. Letting
![]() $e\rightarrow \infty$
shows that
$e\rightarrow \infty$
shows that
![]() $\mathbf{fpt}(f)\geqslant |\boldsymbol{\unicode[STIX]{x1D702}}|=\mathbf{fpt}(\mathfrak{a}_{f})$
, where the last inequality follows from Proposition 36. As the opposite inequality always holds, we have just shown that
$\mathbf{fpt}(f)\geqslant |\boldsymbol{\unicode[STIX]{x1D702}}|=\mathbf{fpt}(\mathfrak{a}_{f})$
, where the last inequality follows from Proposition 36. As the opposite inequality always holds, we have just shown that
![]() $\mathbf{fpt}(f)=\mathbf{fpt}(\mathfrak{a}_{f})$
if
$\mathbf{fpt}(f)=\mathbf{fpt}(\mathfrak{a}_{f})$
if
![]() $L=\infty$
, and it remains to show that the converse holds if
$L=\infty$
, and it remains to show that the converse holds if
![]() $\mathbf{N}$
is in diagonal position, and
$\mathbf{N}$
is in diagonal position, and
![]() $p$
does not divide any denominator in
$p$
does not divide any denominator in
![]() $\boldsymbol{\unicode[STIX]{x1D702}}$
, which we do now. Suppose that
$\boldsymbol{\unicode[STIX]{x1D702}}$
, which we do now. Suppose that
![]() $\mathbf{fpt}(f)=\mathbf{fpt}(\mathfrak{a}_{f})$
. Our hypothesis on
$\mathbf{fpt}(f)=\mathbf{fpt}(\mathfrak{a}_{f})$
. Our hypothesis on
![]() $p$
implies that
$p$
implies that
![]() $(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}$
for infinitely many
$(p^{e}-1)\cdot \boldsymbol{\unicode[STIX]{x1D702}}\in \mathbb{N}$
for infinitely many
![]() $e$
, and for such
$e$
, and for such
![]() $e\geqslant 1$
, Lemma 13 implies that
$e\geqslant 1$
, Lemma 13 implies that
![]() $f^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}\notin \mathfrak{m}^{[p^{e}]}$
. On the other hand, Corollary 39 implies that this occurs if and only if
$f^{(p^{e}-1)\cdot \mathbf{fpt}(\mathfrak{a})}\notin \mathfrak{m}^{[p^{e}]}$
. On the other hand, Corollary 39 implies that this occurs if and only if
Finally, Lemma 3 and Corollary 7 show that this multinomial coefficient is nonzero mod
![]() $p$
if and only if the entries of
$p$
if and only if the entries of
![]() $\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying.
$\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying.
We now address the second point. If
![]() $L<\infty$
, then
$L<\infty$
, then
![]() ${\unicode[STIX]{x1D702}_{1}}^{(L+1)}+\cdots +{\unicode[STIX]{x1D702}_{n}}^{(L+1)}\geqslant p$
, by definition. Consequently, there exist (not necessarily unique) integers
${\unicode[STIX]{x1D702}_{1}}^{(L+1)}+\cdots +{\unicode[STIX]{x1D702}_{n}}^{(L+1)}\geqslant p$
, by definition. Consequently, there exist (not necessarily unique) integers
![]() $\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n}$
such that
$\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n}$
such that
with the second inequality in (5.3) being strict for at least one index. Without loss of generality, we assume that
![]() $\unicode[STIX]{x1D6FF}_{1}<{\unicode[STIX]{x1D702}_{1}}^{(L+1)}$
. For
$\unicode[STIX]{x1D6FF}_{1}<{\unicode[STIX]{x1D702}_{1}}^{(L+1)}$
. For
![]() $e\geqslant 2$
, set
$e\geqslant 2$
, set
We summarize some important properties of
![]() $\boldsymbol{\unicode[STIX]{x1D706}}$
. By construction,
$\boldsymbol{\unicode[STIX]{x1D706}}$
. By construction,
![]() $p^{L+e}\cdot \boldsymbol{\unicode[STIX]{x1D706}}\in \mathbb{N}^{n}$
. Furthermore, the defining properties of the
$p^{L+e}\cdot \boldsymbol{\unicode[STIX]{x1D706}}\in \mathbb{N}^{n}$
. Furthermore, the defining properties of the
![]() $\unicode[STIX]{x1D6FF}_{i}$
show that both
$\unicode[STIX]{x1D6FF}_{i}$
show that both
![]() $\boldsymbol{\unicode[STIX]{x1D706}}\prec \left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}$
and
$\boldsymbol{\unicode[STIX]{x1D706}}\prec \left\langle \boldsymbol{\unicode[STIX]{x1D702}}\right\rangle _{e}$
and
while the definition of
![]() $L$
, and Lemma 6, imply that
$L$
, and Lemma 6, imply that
![]() $\binom{p^{L+e}|\boldsymbol{\unicode[STIX]{x1D706}}|}{p^{L+e}\boldsymbol{\unicode[STIX]{x1D706}}}\neq 0$
modulo
$\binom{p^{L+e}|\boldsymbol{\unicode[STIX]{x1D706}}|}{p^{L+e}\boldsymbol{\unicode[STIX]{x1D706}}}\neq 0$
modulo
![]() $p$
. These properties imply that
$p$
. These properties imply that
![]() $\binom{p^{L+e}|\boldsymbol{\unicode[STIX]{x1D706}}|}{p^{L+e}\boldsymbol{\unicode[STIX]{x1D706}}}u^{p^{L+e}\boldsymbol{\unicode[STIX]{x1D706}}}x^{p^{L+e}\mathbf{E}\boldsymbol{\unicode[STIX]{x1D706}}}$
is a nonzero summand of
$\binom{p^{L+e}|\boldsymbol{\unicode[STIX]{x1D706}}|}{p^{L+e}\boldsymbol{\unicode[STIX]{x1D706}}}u^{p^{L+e}\boldsymbol{\unicode[STIX]{x1D706}}}x^{p^{L+e}\mathbf{E}\boldsymbol{\unicode[STIX]{x1D706}}}$
is a nonzero summand of
![]() $f^{p^{L+e}|\boldsymbol{\unicode[STIX]{x1D706}}|}=f^{p^{L+e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{L}|+p^{e}-1}$
that is not contained in
$f^{p^{L+e}|\boldsymbol{\unicode[STIX]{x1D706}}|}=f^{p^{L+e}|\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{L}|+p^{e}-1}$
that is not contained in
![]() $\mathfrak{m}^{[p^{L+e}]}$
, so that
$\mathfrak{m}^{[p^{L+e}]}$
, so that
![]() $\frac{\unicode[STIX]{x1D708}_{f}\left(p^{L+e}\right)}{p^{L+e}}\geqslant |\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{L}|+\frac{p^{e}-1}{p^{L+e}}$
, and the assertion follows by letting
$\frac{\unicode[STIX]{x1D708}_{f}\left(p^{L+e}\right)}{p^{L+e}}\geqslant |\langle \boldsymbol{\unicode[STIX]{x1D702}}\rangle _{L}|+\frac{p^{e}-1}{p^{L+e}}$
, and the assertion follows by letting
![]() $e\rightarrow \infty$
.◻
$e\rightarrow \infty$
.◻
Remark 43. The estimates given in Theorem 42 can be used to calculate
![]() $\mathbf{fpt}_{\mathfrak{m}}(f)$
in any characteristic whenever
$\mathbf{fpt}_{\mathfrak{m}}(f)$
in any characteristic whenever
![]() $f$
is either a diagonal or binomial hypersurface (see [Reference HernándezHer15, Reference HernándezHer14]).
$f$
is either a diagonal or binomial hypersurface (see [Reference HernándezHer15, Reference HernándezHer14]).
6 Log canonical singularities and (dense/open)
 $F$
-pure type
$F$
-pure type
In this section, we prove our main results relating
![]() $F$
-pure and log canonical thresholds. Although it is not needed in this article, we briefly recall the definition of the log canonical threshold. Given an ideal
$F$
-pure and log canonical thresholds. Although it is not needed in this article, we briefly recall the definition of the log canonical threshold. Given an ideal
![]() $\mathfrak{a}\subseteq \mathbb{C}[x_{1},\ldots ,x_{m}]$
, recall that a log resolution of
$\mathfrak{a}\subseteq \mathbb{C}[x_{1},\ldots ,x_{m}]$
, recall that a log resolution of
![]() $\mathfrak{a}$
consists of a map
$\mathfrak{a}$
consists of a map
![]() $\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{A}_{\mathbb{C}}^{m}$
with the following properties.
$\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{A}_{\mathbb{C}}^{m}$
with the following properties.
-
∙
 $X$
is a smooth variety over
$X$
is a smooth variety over
 $\mathbb{C}$
.
$\mathbb{C}$
. -
∙
 $\unicode[STIX]{x1D70B}$
is a proper, birational map of algebraic varieties.
$\unicode[STIX]{x1D70B}$
is a proper, birational map of algebraic varieties. -
∙
 $\mathfrak{a}\cdot {\mathcal{O}}_{X}$
is invertible, and hence of the form
$\mathfrak{a}\cdot {\mathcal{O}}_{X}$
is invertible, and hence of the form
 ${\mathcal{O}}_{X}(-D)$
for some effective divisor
${\mathcal{O}}_{X}(-D)$
for some effective divisor
 $D$
.
$D$
. -
∙ If
 $E_{\unicode[STIX]{x1D70B}}$
is the exceptional divisor of
$E_{\unicode[STIX]{x1D70B}}$
is the exceptional divisor of
 $\unicode[STIX]{x1D70B}$
, then
$\unicode[STIX]{x1D70B}$
, then
 $E_{\unicode[STIX]{x1D70B}}+D$
has simple normal crossing support.
$E_{\unicode[STIX]{x1D70B}}+D$
has simple normal crossing support.
Given any log resolution, we use
![]() $D_{\unicode[STIX]{x1D70B}}^{\mathfrak{a}}$
to denote an effective divisor on
$D_{\unicode[STIX]{x1D70B}}^{\mathfrak{a}}$
to denote an effective divisor on
![]() $X$
such that
$X$
such that
![]() $\mathfrak{a}\cdot {\mathcal{O}}_{X}={\mathcal{O}}_{X}(-D_{\unicode[STIX]{x1D70B}}^{\mathfrak{a}})$
, and we use
$\mathfrak{a}\cdot {\mathcal{O}}_{X}={\mathcal{O}}_{X}(-D_{\unicode[STIX]{x1D70B}}^{\mathfrak{a}})$
, and we use
![]() $K_{\unicode[STIX]{x1D70B}}$
to denote a relative canonical divisor of
$K_{\unicode[STIX]{x1D70B}}$
to denote a relative canonical divisor of
![]() $\unicode[STIX]{x1D70B}$
(which we may also choose to be effective). Finally, if
$\unicode[STIX]{x1D70B}$
(which we may also choose to be effective). Finally, if
![]() $\mathbf{z}$
is any point in
$\mathbf{z}$
is any point in
![]() $\mathbb{A}_{\mathbb{C}}^{m}$
, and
$\mathbb{A}_{\mathbb{C}}^{m}$
, and
![]() $D=\sum a_{i}\cdot D_{i}$
is any
$D=\sum a_{i}\cdot D_{i}$
is any
![]() $\mathbb{R}$
-divisor on
$\mathbb{R}$
-divisor on
![]() $X$
(here, the sum extends over all prime divisors on
$X$
(here, the sum extends over all prime divisors on
![]() $X$
, so that
$X$
, so that
![]() $a_{i}$
= 0 for almost all
$a_{i}$
= 0 for almost all
![]() $i$
), we say that
$i$
), we say that
![]() $D$
is
$D$
is
![]() $\unicode[STIX]{x1D70B}$
-effective over
$\unicode[STIX]{x1D70B}$
-effective over
![]() $\mathbf{z}$
if the divisor
$\mathbf{z}$
if the divisor
![]() $\sum _{\mathbf{z}\in \unicode[STIX]{x1D70B}(D_{i})}a_{i}\cdot D_{i}$
is effective.
$\sum _{\mathbf{z}\in \unicode[STIX]{x1D70B}(D_{i})}a_{i}\cdot D_{i}$
is effective.
Definition 44. Fix an ideal
![]() $\mathfrak{a}\subseteq \mathbb{C}[x_{1},\ldots ,x_{m}]$
with
$\mathfrak{a}\subseteq \mathbb{C}[x_{1},\ldots ,x_{m}]$
with
![]() $\mathbf{0}\in \mathbb{V}(\mathfrak{a})$
, and consider a log resolution
$\mathbf{0}\in \mathbb{V}(\mathfrak{a})$
, and consider a log resolution
![]() $\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{A}_{\mathbb{C}}^{m}$
of
$\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{A}_{\mathbb{C}}^{m}$
of
![]() $\mathfrak{a}$
. The log canonical threshold of
$\mathfrak{a}$
. The log canonical threshold of
![]() $\mathfrak{a}$
at the origin is defined as
$\mathfrak{a}$
at the origin is defined as
In the case that
![]() $\mathfrak{a}$
is a principal ideal generated by
$\mathfrak{a}$
is a principal ideal generated by
![]() $f$
, we write
$f$
, we write
![]() $\mathbf{lct}(f)$
instead of
$\mathbf{lct}(f)$
instead of
![]() $\mathbf{lct}(\mathfrak{a})$
.
$\mathbf{lct}(\mathfrak{a})$
.
The log canonical threshold turns out to not depend on the choice of log resolution. Moreover,
![]() $\mathbf{lct}(\mathfrak{a})$
is always a rational number, and the log canonical threshold of a principal ideal is always contained in
$\mathbf{lct}(\mathfrak{a})$
is always a rational number, and the log canonical threshold of a principal ideal is always contained in
![]() $(0,1]$
. Furthermore, if
$(0,1]$
. Furthermore, if
![]() $f\in \mathfrak{a}$
, then
$f\in \mathfrak{a}$
, then
![]() $\mathbf{lct}(f)\leqslant \mathbf{lct}(\mathfrak{a})$
. For justification of these facts, and for more references to the theory of log canonical thresholds (and related topics), we refer the reader to the surveys [Reference Blickle and LazarsfeldBL04, Reference Ein and Mustaţă EM06, Reference Benito, Faber and SmithBFS13]. In what follows, we summarize all of the properties of log canonical thresholds that we need in this article.
$\mathbf{lct}(f)\leqslant \mathbf{lct}(\mathfrak{a})$
. For justification of these facts, and for more references to the theory of log canonical thresholds (and related topics), we refer the reader to the surveys [Reference Blickle and LazarsfeldBL04, Reference Ein and Mustaţă EM06, Reference Benito, Faber and SmithBFS13]. In what follows, we summarize all of the properties of log canonical thresholds that we need in this article.
Proposition 45. Let
![]() $f\in \mathbb{C}[x_{1},\ldots ,x_{m}]$
be a polynomial vanishing at the origin, and let
$f\in \mathbb{C}[x_{1},\ldots ,x_{m}]$
be a polynomial vanishing at the origin, and let
![]() $\mathfrak{a}_{f}$
denote its term ideal, so that
$\mathfrak{a}_{f}$
denote its term ideal, so that
![]() $\mathbf{0}$
is contained in both the vanishing set of
$\mathbf{0}$
is contained in both the vanishing set of
![]() $f$
and
$f$
and
![]() $\mathfrak{a}_{f}$
.
$\mathfrak{a}_{f}$
.
-
(1)
 $\mathbf{lct}(f)$
and
$\mathbf{lct}(f)$
and
 $\mathbf{lct}(\mathfrak{a}_{f})$
are rational numbers, with
$\mathbf{lct}(\mathfrak{a}_{f})$
are rational numbers, with
 $\mathbf{lct}(f)\leqslant \min \left\{1,\mathbf{lct}(\mathfrak{a}_{f})\right\}$
.
$\mathbf{lct}(f)\leqslant \min \left\{1,\mathbf{lct}(\mathfrak{a}_{f})\right\}$
. -
(2) If
 $\mathbf{N}$
denotes the Newton polyhedron associated to
$\mathbf{N}$
denotes the Newton polyhedron associated to
 $f$
, then
$f$
, then  $$\begin{eqnarray}\mathbf{lct}(\mathfrak{a}_{f})=\max \left\{\unicode[STIX]{x1D706}>0:\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}\in \mathbf{N}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{lct}(\mathfrak{a}_{f})=\max \left\{\unicode[STIX]{x1D706}>0:\frac{1}{\unicode[STIX]{x1D706}}\cdot \mathbf{1}_{m}\in \mathbf{N}\right\}.\end{eqnarray}$$
Proof. The first point follows from the preceding discussion, while the second appears in [Reference HowaldHow01a]. ◻
Corollary 46. If
![]() $\mathbb{L}$
is a field of characteristic
$\mathbb{L}$
is a field of characteristic
![]() $p>0$
, and if
$p>0$
, and if
![]() $f\in \mathbb{C}[x_{1},\ldots ,x_{m}]$
and
$f\in \mathbb{C}[x_{1},\ldots ,x_{m}]$
and
![]() $f_{p}\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
are polynomials vanishing at the origin with
$f_{p}\in \mathbb{L}[x_{1},\ldots ,x_{m}]$
are polynomials vanishing at the origin with
![]() $\text{Supp}(f)=\text{Supp}(f_{p})$
, then
$\text{Supp}(f)=\text{Supp}(f_{p})$
, then
![]() $\mathbf{fpt}(\mathfrak{a}_{f})=\mathbf{lct}(\mathfrak{a}_{f_{p}})$
.
$\mathbf{fpt}(\mathfrak{a}_{f})=\mathbf{lct}(\mathfrak{a}_{f_{p}})$
.
Proof. This result is a restatement of [Reference Hara and YoshidaHY03, Theorem 6.10(3)]. For a self-contained proof, compare the description of
![]() $\mathbf{lct}(\mathfrak{a}_{f})$
given in Proposition 45 with the description of
$\mathbf{lct}(\mathfrak{a}_{f})$
given in Proposition 45 with the description of
![]() $\mathbf{fpt}(\mathfrak{a}_{f_{p}})$
given in Proposition 36.◻
$\mathbf{fpt}(\mathfrak{a}_{f_{p}})$
given in Proposition 36.◻
6.1 On reduction to positive characteristic
In this subsection, we discuss the process of reduction to positive characteristic. Many of the technical steps that follow depend on the following well-known lemma.
Lemma 47. Let
![]() $A$
be a finitely generated algebra over a domain
$A$
be a finitely generated algebra over a domain
![]() $D\subseteq A$
. There exists a nonzero element
$D\subseteq A$
. There exists a nonzero element
![]() $N\in D$
such that
$N\in D$
such that
![]() $D_{N}\subseteq A_{N}$
factors as
$D_{N}\subseteq A_{N}$
factors as
![]() $D_{N}\subseteq D_{N}[z_{1},\ldots ,z_{d}]\subseteq A_{N}$
, where
$D_{N}\subseteq D_{N}[z_{1},\ldots ,z_{d}]\subseteq A_{N}$
, where
![]() $z_{1},\ldots ,z_{d}$
are algebraically independent over
$z_{1},\ldots ,z_{d}$
are algebraically independent over
![]() $D_{N}$
, and
$D_{N}$
, and
![]() $D_{N}[z_{1},\ldots ,z_{d}]\subseteq A_{N}$
is finite.
$D_{N}[z_{1},\ldots ,z_{d}]\subseteq A_{N}$
is finite.
Proof. If
![]() $L=\text{Frac}D$
, and
$L=\text{Frac}D$
, and
![]() $R$
is the localization of
$R$
is the localization of
![]() $A$
at the nonzero elements of
$A$
at the nonzero elements of
![]() $D$
, then Lemma 47 can be obtained by applying the Noether normalization theorem to the inclusion
$D$
, then Lemma 47 can be obtained by applying the Noether normalization theorem to the inclusion
![]() $L\subseteq R$
. The reader is referred to the author’s thesis [Reference HernándezHer11] for more details.◻
$L\subseteq R$
. The reader is referred to the author’s thesis [Reference HernándezHer11] for more details.◻
Corollary 48. If
![]() $A$
is a finitely generated
$A$
is a finitely generated
![]() $\mathbb{Z}$
-algebra, then
$\mathbb{Z}$
-algebra, then
![]() $A/\unicode[STIX]{x1D707}$
is a finite field for every maximal ideal
$A/\unicode[STIX]{x1D707}$
is a finite field for every maximal ideal
![]() $\unicode[STIX]{x1D707}\subseteq A$
. Furthermore, all but finitely many primes
$\unicode[STIX]{x1D707}\subseteq A$
. Furthermore, all but finitely many primes
![]() $p\in \mathbb{Z}$
are contained in a maximal ideal of
$p\in \mathbb{Z}$
are contained in a maximal ideal of
![]() $A$
.
$A$
.
Proof. This follows from Lemma 47, and we refer the reader to the author’s thesis [Reference HernándezHer11] for a detailed proof. ◻
Suppose that
![]() $f\in \mathbb{C}[x_{1},\ldots ,x_{m}]$
is a polynomial vanishing at the origin, and let
$f\in \mathbb{C}[x_{1},\ldots ,x_{m}]$
is a polynomial vanishing at the origin, and let
![]() $A\subseteq \mathbb{C}$
be a finitely generated
$A\subseteq \mathbb{C}$
be a finitely generated
![]() $\mathbb{Z}$
-algebra containing the coefficients of
$\mathbb{Z}$
-algebra containing the coefficients of
![]() $f$
, so that
$f$
, so that
![]() $f\in A[x_{1},\ldots ,x_{m}]$
. For such an algebra, it follows from Corollary 48 that
$f\in A[x_{1},\ldots ,x_{m}]$
. For such an algebra, it follows from Corollary 48 that
![]() $A/\unicode[STIX]{x1D707}$
is a finite field for every
$A/\unicode[STIX]{x1D707}$
is a finite field for every
![]() $\unicode[STIX]{x1D707}\in \text{mSpec}A$
, and all but finitely many primes appear in the set
$\unicode[STIX]{x1D707}\in \text{mSpec}A$
, and all but finitely many primes appear in the set
![]() $\left\{\text{char}A/\unicode[STIX]{x1D707}:\unicode[STIX]{x1D707}\in \text{mSpec}A\right\}$
. Let
$\left\{\text{char}A/\unicode[STIX]{x1D707}:\unicode[STIX]{x1D707}\in \text{mSpec}A\right\}$
. Let
![]() $f_{\unicode[STIX]{x1D707}}$
denote the image of
$f_{\unicode[STIX]{x1D707}}$
denote the image of
![]() $f$
in
$f$
in
![]() $\left(A/\unicode[STIX]{x1D707}\right)[x_{1},\ldots ,x_{m}]$
. Furthermore, we may enlarge
$\left(A/\unicode[STIX]{x1D707}\right)[x_{1},\ldots ,x_{m}]$
. Furthermore, we may enlarge
![]() $A$
(say, by adjoining the inverses of the coefficients of
$A$
(say, by adjoining the inverses of the coefficients of
![]() $f$
) so as to assume that
$f$
) so as to assume that
![]() $\text{Supp}(f_{\unicode[STIX]{x1D707}})=\text{Supp}(f)$
for every
$\text{Supp}(f_{\unicode[STIX]{x1D707}})=\text{Supp}(f)$
for every
![]() $\unicode[STIX]{x1D707}\in \text{mSpec}A$
. We call
$\unicode[STIX]{x1D707}\in \text{mSpec}A$
. We call
![]() $\left\{f_{\unicode[STIX]{x1D707}}:\unicode[STIX]{x1D707}\in \text{mSpec}A\right\}$
a family of positive characteristic models of
$\left\{f_{\unicode[STIX]{x1D707}}:\unicode[STIX]{x1D707}\in \text{mSpec}A\right\}$
a family of positive characteristic models of
![]() $f$
.
$f$
.
Corollary 49. If
![]() $A$
is a finitely generated algebra over a domain
$A$
is a finitely generated algebra over a domain
![]() $D\subseteq A$
, then the inverse image of a dense set under the induced map
$D\subseteq A$
, then the inverse image of a dense set under the induced map
![]() $\text{Spec}A\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }\text{Spec}D$
is also dense.
$\text{Spec}A\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }\text{Spec}D$
is also dense.
Proof. Let
![]() $\mathscr{D}$
be dense in
$\mathscr{D}$
be dense in
![]() $\text{Spec}D$
. It suffices to show that
$\text{Spec}D$
. It suffices to show that
![]() $\text{Spec}A_{f}\cap \unicode[STIX]{x1D70B}^{-1}(\mathscr{D})$
is nonempty for every nonzero
$\text{Spec}A_{f}\cap \unicode[STIX]{x1D70B}^{-1}(\mathscr{D})$
is nonempty for every nonzero
![]() $f\in A$
. As
$f\in A$
. As
![]() $A$
is finitely generated over
$A$
is finitely generated over
![]() $D$
, so is
$D$
, so is
![]() $A_{f}=A[T]/(1-Tf)$
. Consider a factorization
$A_{f}=A[T]/(1-Tf)$
. Consider a factorization
![]() $D_{N}\subseteq D_{N}[z_{1},\ldots ,z_{d}]\subseteq A_{fN}$
as in Lemma 47. By the lying over theorem,
$D_{N}\subseteq D_{N}[z_{1},\ldots ,z_{d}]\subseteq A_{fN}$
as in Lemma 47. By the lying over theorem,
![]() $\text{Spec}A_{fN}\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }\text{Spec}D_{N}$
is surjective. As
$\text{Spec}A_{fN}\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }\text{Spec}D_{N}$
is surjective. As
![]() $\mathscr{D}$
is dense,
$\mathscr{D}$
is dense,
![]() $\mathscr{D}\cap \text{Spec}D_{N}=\mathscr{D}\cap \unicode[STIX]{x1D70B}(\text{Spec}A_{fN})$
is nonempty. Consequently,
$\mathscr{D}\cap \text{Spec}D_{N}=\mathscr{D}\cap \unicode[STIX]{x1D70B}(\text{Spec}A_{fN})$
is nonempty. Consequently,
![]() $\text{Spec}A_{fN}\cap \unicode[STIX]{x1D70B}^{-1}(\mathscr{D})$
, and hence
$\text{Spec}A_{fN}\cap \unicode[STIX]{x1D70B}^{-1}(\mathscr{D})$
, and hence
![]() $\text{Spec}A_{f}\cap \unicode[STIX]{x1D70B}^{-1}(\mathscr{D})$
, is nonempty.◻
$\text{Spec}A_{f}\cap \unicode[STIX]{x1D70B}^{-1}(\mathscr{D})$
, is nonempty.◻
6.2 Connections with
 $F$
-pure thresholds
$F$
-pure thresholds
Notation 50. Set
![]() $S=\mathbb{C}[x_{1},\ldots ,x_{m}]$
. If
$S=\mathbb{C}[x_{1},\ldots ,x_{m}]$
. If
![]() $A$
is a finitely generated
$A$
is a finitely generated
![]() $\mathbb{Z}$
subalgebra of
$\mathbb{Z}$
subalgebra of
![]() $\mathbb{C}$
, we use
$\mathbb{C}$
, we use
![]() $S_{A}$
to denote the subring
$S_{A}$
to denote the subring
![]() $A[x_{1},\ldots ,x_{m}]\subseteq S$
. Note that
$A[x_{1},\ldots ,x_{m}]\subseteq S$
. Note that
![]() $\mathbb{C}\otimes _{A}S_{A}=S$
. If
$\mathbb{C}\otimes _{A}S_{A}=S$
. If
![]() $\unicode[STIX]{x1D707}$
is a maximal ideal of
$\unicode[STIX]{x1D707}$
is a maximal ideal of
![]() $A$
,
$A$
,
![]() $S_{A}(\unicode[STIX]{x1D707})$
denotes the polynomial ring
$S_{A}(\unicode[STIX]{x1D707})$
denotes the polynomial ring
![]() $S_{A}\otimes _{A}A/\unicode[STIX]{x1D707}=S_{A}/\unicode[STIX]{x1D707}S_{A}=\left(A/\unicode[STIX]{x1D707}\right)[x_{1},\ldots ,x_{m}]$
. By Corollary 48,
$S_{A}\otimes _{A}A/\unicode[STIX]{x1D707}=S_{A}/\unicode[STIX]{x1D707}S_{A}=\left(A/\unicode[STIX]{x1D707}\right)[x_{1},\ldots ,x_{m}]$
. By Corollary 48,
![]() $\text{char}S_{A}(\unicode[STIX]{x1D707})>0$
. For
$\text{char}S_{A}(\unicode[STIX]{x1D707})>0$
. For
![]() $f\in S_{A}$
, we use
$f\in S_{A}$
, we use
![]() $f_{\unicode[STIX]{x1D707}}$
to denote the image of
$f_{\unicode[STIX]{x1D707}}$
to denote the image of
![]() $f$
in
$f$
in
![]() $S_{A}(\unicode[STIX]{x1D707})$
. Finally,
$S_{A}(\unicode[STIX]{x1D707})$
. Finally,
![]() $\mathfrak{m}$
denotes the ideal generated by the variables
$\mathfrak{m}$
denotes the ideal generated by the variables
![]() $x_{1},\ldots ,x_{m}$
in the polynomial rings
$x_{1},\ldots ,x_{m}$
in the polynomial rings
![]() $S,S_{A}$
, and
$S,S_{A}$
, and
![]() $S_{A}(\unicode[STIX]{x1D707})$
.
$S_{A}(\unicode[STIX]{x1D707})$
.
It is an important fact that the
![]() $F$
-pure (respectively, log canonical) threshold of a polynomial may also be defined in terms of its associated test ideals (respectively, multiplier ideals). Theorem 51 below was first observed in [Reference Mustaţǎ, Takagi and WatanabeMTW05, Theorem 3.4], and follows from deep theorems in [Reference SmithSmi00, Reference Hara and YoshidaHY03] relating test ideals and multiplier ideals. We refer the reader to the author’s thesis [Reference HernándezHer11] for a detailed proof.
$F$
-pure (respectively, log canonical) threshold of a polynomial may also be defined in terms of its associated test ideals (respectively, multiplier ideals). Theorem 51 below was first observed in [Reference Mustaţǎ, Takagi and WatanabeMTW05, Theorem 3.4], and follows from deep theorems in [Reference SmithSmi00, Reference Hara and YoshidaHY03] relating test ideals and multiplier ideals. We refer the reader to the author’s thesis [Reference HernándezHer11] for a detailed proof.
Theorem 51. Let
![]() $f\in S$
be a polynomial vanishing at the origin. Then, for every finitely generated
$f\in S$
be a polynomial vanishing at the origin. Then, for every finitely generated
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $A\subseteq \mathbb{C}$
with
$A\subseteq \mathbb{C}$
with
![]() $f\in S_{A}$
, the following hold.
$f\in S_{A}$
, the following hold.
-
(1) There exists a dense open set
 $U\subseteq \text{Spec}A$
such that
$U\subseteq \text{Spec}A$
such that
 $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})\leqslant \mathbf{lct}(f)$
for every maximal ideal
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})\leqslant \mathbf{lct}(f)$
for every maximal ideal
 $\unicode[STIX]{x1D707}\in U$
.
$\unicode[STIX]{x1D707}\in U$
. -
(2) For every
 $0<\unicode[STIX]{x1D706}<\mathbf{lct}(f)$
, there exists a dense open set
$0<\unicode[STIX]{x1D706}<\mathbf{lct}(f)$
, there exists a dense open set
 $U_{\unicode[STIX]{x1D706}}\subseteq \text{Spec}A$
such that
$U_{\unicode[STIX]{x1D706}}\subseteq \text{Spec}A$
such that
 $\unicode[STIX]{x1D706}\leqslant \mathbf{fpt}(f_{\unicode[STIX]{x1D707}})\leqslant \mathbf{lct}(f)$
for every maximal ideal
$\unicode[STIX]{x1D706}\leqslant \mathbf{fpt}(f_{\unicode[STIX]{x1D707}})\leqslant \mathbf{lct}(f)$
for every maximal ideal
 $\unicode[STIX]{x1D707}\in U_{\unicode[STIX]{x1D706}}$
.
$\unicode[STIX]{x1D707}\in U_{\unicode[STIX]{x1D706}}$
.
We stress that the open set
![]() $U_{\unicode[STIX]{x1D706}}$
depends on
$U_{\unicode[STIX]{x1D706}}$
depends on
![]() $\unicode[STIX]{x1D706}$
, and often shrinks as
$\unicode[STIX]{x1D706}$
, and often shrinks as
![]() $\unicode[STIX]{x1D706}$
increases.
$\unicode[STIX]{x1D706}$
increases.
Remark 52. Suppose that
![]() $f$
has integer coefficients. If
$f$
has integer coefficients. If
![]() $f_{p}$
denotes the image of
$f_{p}$
denotes the image of
![]() $f$
in
$f$
in
![]() $\mathbb{F}_{p}[x_{1},\ldots ,x_{m}]$
, the statements of Theorem 51 become
$\mathbb{F}_{p}[x_{1},\ldots ,x_{m}]$
, the statements of Theorem 51 become
Definition 53. Let
![]() $f\in S$
be a polynomial vanishing at the origin. We say that log canonicity equals dense (respectively, open)
$f\in S$
be a polynomial vanishing at the origin. We say that log canonicity equals dense (respectively, open)
![]() $F$
-pure type (at the origin) for
$F$
-pure type (at the origin) for
![]() $f$
if for every finitely generated
$f$
if for every finitely generated
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $A\subseteq \mathbb{C}$
with
$A\subseteq \mathbb{C}$
with
![]() $f\in S_{A}$
, there exists a dense (respectively, nonempty open) subset
$f\in S_{A}$
, there exists a dense (respectively, nonempty open) subset
![]() $W\subseteq \text{Spec}A$
such that
$W\subseteq \text{Spec}A$
such that
![]() $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)$
for every maximal ideal
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)$
for every maximal ideal
![]() $\unicode[STIX]{x1D707}\in W$
.
$\unicode[STIX]{x1D707}\in W$
.
Remark 54. To show that log canonicity equals (open/dense)
![]() $F$
-pure type for
$F$
-pure type for
![]() $f$
, it suffices to produce a single finitely generated
$f$
, it suffices to produce a single finitely generated
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $A$
satisfying the conditions of Definition 53. We refer the reader to the author’s thesis [Reference HernándezHer11] for a detailed verification of this.
$A$
satisfying the conditions of Definition 53. We refer the reader to the author’s thesis [Reference HernándezHer11] for a detailed verification of this.
Remark 55. In the study of singularities of pairs, the terms log canonical and
![]() $F$
-pure have their own independent meaningsFootnote
1
. Indeed, one defines the notion of log singularities for pairs
$F$
-pure have their own independent meaningsFootnote
1
. Indeed, one defines the notion of log singularities for pairs
![]() $\left(S,\unicode[STIX]{x1D706}\bullet f\right)$
via resolution of singularities (or via integrability conditions) (see [Reference LazarsfeldLaz04]). Additionally, we have that
$\left(S,\unicode[STIX]{x1D706}\bullet f\right)$
via resolution of singularities (or via integrability conditions) (see [Reference LazarsfeldLaz04]). Additionally, we have that
which justifies the use of the term log canonical threshold. In the positive characteristic setting, one defines the notion of
![]() $F$
-purity for pairs via the Frobenius morphism, and we again have that the
$F$
-purity for pairs via the Frobenius morphism, and we again have that the
![]() $F$
-pure threshold of a polynomial is the supremum over all parameters such that the corresponding pair is
$F$
-pure threshold of a polynomial is the supremum over all parameters such that the corresponding pair is
![]() $F$
-pure (see [Reference Hara and WatanabeHW02, Reference Takagi and WatanabeTW04]). We say that the pair
$F$
-pure (see [Reference Hara and WatanabeHW02, Reference Takagi and WatanabeTW04]). We say that the pair
![]() $\left(S,\unicode[STIX]{x1D706}\bullet f\right)$
is of dense (respectively, open)
$\left(S,\unicode[STIX]{x1D706}\bullet f\right)$
is of dense (respectively, open)
![]() $F$
-pure type (at the origin) if for every (equivalently, for some) finitely generated
$F$
-pure type (at the origin) if for every (equivalently, for some) finitely generated
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $A\subseteq \mathbb{C}$
with
$A\subseteq \mathbb{C}$
with
![]() $f\in S_{A}$
, there exists a dense (respectively, nonempty open) set
$f\in S_{A}$
, there exists a dense (respectively, nonempty open) set
![]() $W\subseteq \text{Spec}A$
such that the pair
$W\subseteq \text{Spec}A$
such that the pair
![]() $\left(S_{A}(\unicode[STIX]{x1D707}),\unicode[STIX]{x1D706}\bullet f_{\unicode[STIX]{x1D707}}\right)$
is
$\left(S_{A}(\unicode[STIX]{x1D707}),\unicode[STIX]{x1D706}\bullet f_{\unicode[STIX]{x1D707}}\right)$
is
![]() $F$
-pure for every maximal ideal
$F$
-pure for every maximal ideal
![]() $\unicode[STIX]{x1D707}\in W$
. It is shown in [Reference Hara and WatanabeHW02, Reference TakagiTak04] that if
$\unicode[STIX]{x1D707}\in W$
. It is shown in [Reference Hara and WatanabeHW02, Reference TakagiTak04] that if
![]() $\left(S,\unicode[STIX]{x1D706}\bullet f\right)$
is of dense
$\left(S,\unicode[STIX]{x1D706}\bullet f\right)$
is of dense
![]() $F$
-pure type, then it is also log canonical. It is an important, yet easy to verify, property of log canonicity that
$F$
-pure type, then it is also log canonical. It is an important, yet easy to verify, property of log canonicity that
![]() $\left(S,\mathbf{lct}(f)\bullet f\right)$
is log canonical. Consequently,
$\left(S,\mathbf{lct}(f)\bullet f\right)$
is log canonical. Consequently,
![]() $\left(S,\unicode[STIX]{x1D706}\bullet f\right)$
is log canonical if and only if
$\left(S,\unicode[STIX]{x1D706}\bullet f\right)$
is log canonical if and only if
![]() $0\leqslant \unicode[STIX]{x1D706}\leqslant \mathbf{lct}(f)$
. In prime characteristic, that a pair is
$0\leqslant \unicode[STIX]{x1D706}\leqslant \mathbf{lct}(f)$
. In prime characteristic, that a pair is
![]() $F$
-pure at the threshold is shown in [Reference HaraHar06, Reference HernándezHer12], and it follows that the reductions
$F$
-pure at the threshold is shown in [Reference HaraHar06, Reference HernándezHer12], and it follows that the reductions
![]() $\left(S_{A}(\unicode[STIX]{x1D707}),\unicode[STIX]{x1D706}\bullet f_{\unicode[STIX]{x1D707}}\right)$
are
$\left(S_{A}(\unicode[STIX]{x1D707}),\unicode[STIX]{x1D706}\bullet f_{\unicode[STIX]{x1D707}}\right)$
are
![]() $F$
-pure if and only if
$F$
-pure if and only if
![]() $0\leqslant \unicode[STIX]{x1D706}\leqslant \mathbf{fpt}(f_{\unicode[STIX]{x1D707}})$
. Examining the definitions, we reach the following conclusion. To show that log canonicity is equivalent to dense (respectively, open)
$0\leqslant \unicode[STIX]{x1D706}\leqslant \mathbf{fpt}(f_{\unicode[STIX]{x1D707}})$
. Examining the definitions, we reach the following conclusion. To show that log canonicity is equivalent to dense (respectively, open)
![]() $F$
-pure type for pairs
$F$
-pure type for pairs
![]() $\left(S,\unicode[STIX]{x1D706}\bullet f\right)$
, it suffices to show that
$\left(S,\unicode[STIX]{x1D706}\bullet f\right)$
, it suffices to show that
![]() $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)$
for all maximal
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)$
for all maximal
![]() $\unicode[STIX]{x1D707}$
in some dense (respectively, nonempty open) subset of
$\unicode[STIX]{x1D707}$
in some dense (respectively, nonempty open) subset of
![]() $\text{Spec}A$
, which justifies our choice of terminology in Definition 53.
$\text{Spec}A$
, which justifies our choice of terminology in Definition 53.
Theorem 56. Fix a polynomial
![]() $f\in S=\mathbb{C}[x_{1},\ldots ,x_{m}]$
vanishing at the origin, and suppose that the splitting polytope
$f\in S=\mathbb{C}[x_{1},\ldots ,x_{m}]$
vanishing at the origin, and suppose that the splitting polytope
![]() $\mathbf{P}$
associated to
$\mathbf{P}$
associated to
![]() $f$
contains a unique maximal point
$f$
contains a unique maximal point
![]() $\boldsymbol{\unicode[STIX]{x1D702}}$
. If
$\boldsymbol{\unicode[STIX]{x1D702}}$
. If
![]() $A\subseteq \mathbb{C}$
is any finitely generated
$A\subseteq \mathbb{C}$
is any finitely generated
![]() $\mathbb{Z}$
-algebra containing the coefficients of
$\mathbb{Z}$
-algebra containing the coefficients of
![]() $f$
, then the following hold.
$f$
, then the following hold.
-
(1) If
 $\mathbf{lct}(\mathfrak{a}_{f})>1$
, then
$\mathbf{lct}(\mathfrak{a}_{f})>1$
, then
 $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)=1$
for all
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)=1$
for all
 $\unicode[STIX]{x1D707}\in \text{mSpec}A$
with
$\unicode[STIX]{x1D707}\in \text{mSpec}A$
with
 $\text{char}S_{A}(\unicode[STIX]{x1D707})\gg 0$
. In particular, log canonicity equals open
$\text{char}S_{A}(\unicode[STIX]{x1D707})\gg 0$
. In particular, log canonicity equals open
 $F$
-pure type for
$F$
-pure type for
 $f$
.
$f$
. -
(2) If
 $\mathbf{lct}(\mathfrak{a}_{f})\leqslant 1$
, then for all maximal ideals
$\mathbf{lct}(\mathfrak{a}_{f})\leqslant 1$
, then for all maximal ideals
 $\unicode[STIX]{x1D707}\in \text{mSpec}A$
with
$\unicode[STIX]{x1D707}\in \text{mSpec}A$
with
 $\text{char}S_{A}(\unicode[STIX]{x1D707})\gg 0$
, whenever the entries of
$\text{char}S_{A}(\unicode[STIX]{x1D707})\gg 0$
, whenever the entries of $$\begin{eqnarray}\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)\end{eqnarray}$$
 $\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying (base
$\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying (base
 $\text{char}S_{A}(\unicode[STIX]{x1D707})$
). If, in addition, the Newton polyhedron associated to
$\text{char}S_{A}(\unicode[STIX]{x1D707})$
). If, in addition, the Newton polyhedron associated to
 $f$
is in diagonal position, then
$f$
is in diagonal position, then
 $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)$
if and only if the entries of
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)$
if and only if the entries of
 $\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying (base
$\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying (base
 $\text{char}S_{A}(\unicode[STIX]{x1D707})$
). In particular, log canonicity equals dense
$\text{char}S_{A}(\unicode[STIX]{x1D707})$
). In particular, log canonicity equals dense
 $F$
-pure type for
$F$
-pure type for
 $f$
.
$f$
.
Proof. Let
![]() $A$
be such that
$A$
be such that
![]() $f\in S_{A}$
, and consider the map
$f\in S_{A}$
, and consider the map
![]() $\text{Spec}A\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }\text{Spec}\mathbb{Z}$
. After enlarging
$\text{Spec}A\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }\text{Spec}\mathbb{Z}$
. After enlarging
![]() $A$
, we may assume that
$A$
, we may assume that
![]() $\text{Supp}(f_{\unicode[STIX]{x1D707}})=\text{Supp}(f)$
for every
$\text{Supp}(f_{\unicode[STIX]{x1D707}})=\text{Supp}(f)$
for every
![]() $\unicode[STIX]{x1D707}\in \text{mSpec}A$
, and, hence, that
$\unicode[STIX]{x1D707}\in \text{mSpec}A$
, and, hence, that
![]() $|\boldsymbol{\unicode[STIX]{x1D702}}|=\mathbf{fpt}(a_{f_{\unicode[STIX]{x1D707}}})=\mathbf{lct}(\mathfrak{a}_{f})$
. First, suppose that
$|\boldsymbol{\unicode[STIX]{x1D702}}|=\mathbf{fpt}(a_{f_{\unicode[STIX]{x1D707}}})=\mathbf{lct}(\mathfrak{a}_{f})$
. First, suppose that
![]() $|\boldsymbol{\unicode[STIX]{x1D702}}|>1$
. By Lemma 8, there exists a nonempty open subset
$|\boldsymbol{\unicode[STIX]{x1D702}}|>1$
. By Lemma 8, there exists a nonempty open subset
![]() $U\subseteq \text{Spec}\mathbb{Z}$
such that
$U\subseteq \text{Spec}\mathbb{Z}$
such that
![]() ${\unicode[STIX]{x1D702}_{1}}^{(1)}+\cdots +{\unicode[STIX]{x1D702}_{n}}^{(1)}\geqslant p$
for every
${\unicode[STIX]{x1D702}_{1}}^{(1)}+\cdots +{\unicode[STIX]{x1D702}_{n}}^{(1)}\geqslant p$
for every
![]() $p\in U$
. For such primes, it follows that
$p\in U$
. For such primes, it follows that
![]() $L=0$
in Theorem 42, which then states that
$L=0$
in Theorem 42, which then states that
![]() $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})\geqslant 1$
for every
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})\geqslant 1$
for every
![]() $p\in U$
and
$p\in U$
and
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D70B}^{-1}(U)$
. Since
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D70B}^{-1}(U)$
. Since
![]() $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})\leqslant 1$
always, we see that
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})\leqslant 1$
always, we see that
![]() $1=\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})\leqslant \mathbf{lct}(f)\leqslant 1$
for every
$1=\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})\leqslant \mathbf{lct}(f)\leqslant 1$
for every
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D70B}^{-1}(U)$
, which is a nonempty open set, by Corollary 48. We conclude that log canonicity equals open
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D70B}^{-1}(U)$
, which is a nonempty open set, by Corollary 48. We conclude that log canonicity equals open
![]() $F$
-pure type for
$F$
-pure type for
![]() $f$
.
$f$
.
Next, suppose that
![]() $|\boldsymbol{\unicode[STIX]{x1D702}}|\leqslant 1$
, and let
$|\boldsymbol{\unicode[STIX]{x1D702}}|\leqslant 1$
, and let
![]() $\mathscr{P}$
denote the set of all primes
$\mathscr{P}$
denote the set of all primes
![]() $p$
such that the entries of
$p$
such that the entries of
![]() $\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying (base
$\boldsymbol{\unicode[STIX]{x1D702}}$
add without carrying (base
![]() $p$
). By Lemma 8, the set
$p$
). By Lemma 8, the set
![]() $\mathscr{P}$
is infinite, and by Corollary 49,
$\mathscr{P}$
is infinite, and by Corollary 49,
![]() $\unicode[STIX]{x1D70B}^{-1}(\mathscr{P})$
is a dense subset of
$\unicode[STIX]{x1D70B}^{-1}(\mathscr{P})$
is a dense subset of
![]() $\text{Spec}A$
. Moreover, Theorem 42 states that, if
$\text{Spec}A$
. Moreover, Theorem 42 states that, if
![]() $\text{char}S_{A}(\unicode[STIX]{x1D707})\gg 0$
, then
$\text{char}S_{A}(\unicode[STIX]{x1D707})\gg 0$
, then
![]() $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}}})$
whenever
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}}})$
whenever
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D70B}^{-1}(\mathscr{P})$
. Theorem 42 also shows that, if
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D70B}^{-1}(\mathscr{P})$
. Theorem 42 also shows that, if
![]() $\text{char}S_{A}(\unicode[STIX]{x1D707})\gg 0$
and
$\text{char}S_{A}(\unicode[STIX]{x1D707})\gg 0$
and
![]() $\mathbf{N}_{\mathfrak{a}_{f}}$
is in diagonal position, then
$\mathbf{N}_{\mathfrak{a}_{f}}$
is in diagonal position, then
![]() $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}}})$
if and only if
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}}})$
if and only if
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D70B}^{-1}(\mathscr{P})$
. Finally, the string of inequalities
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D70B}^{-1}(\mathscr{P})$
. Finally, the string of inequalities
shows that all of these thresholds agree whenever
![]() $\text{char}S_{A}(\unicode[STIX]{x1D707})\gg 0$
and
$\text{char}S_{A}(\unicode[STIX]{x1D707})\gg 0$
and
![]() $\unicode[STIX]{x1D707}$
is contained in the dense subset
$\unicode[STIX]{x1D707}$
is contained in the dense subset
![]() $\unicode[STIX]{x1D70B}^{-1}(\mathscr{P})$
. We conclude that log canonicity equals dense
$\unicode[STIX]{x1D70B}^{-1}(\mathscr{P})$
. We conclude that log canonicity equals dense
![]() $F$
-pure type for
$F$
-pure type for
![]() $f$
.◻
$f$
.◻
Lemma 57. If
![]() $f\in S=\mathbb{C}[x_{1},\ldots ,x_{m}]$
is a polynomial vanishing at the origin, then log canonicity equals dense
$f\in S=\mathbb{C}[x_{1},\ldots ,x_{m}]$
is a polynomial vanishing at the origin, then log canonicity equals dense
![]() $F$
-pure type for
$F$
-pure type for
![]() $f$
if there exist a finitely generated
$f$
if there exist a finitely generated
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $A\subseteq \mathbb{C}$
with
$A\subseteq \mathbb{C}$
with
![]() $f\in S_{A}$
, an infinite set of primes
$f\in S_{A}$
, an infinite set of primes
![]() $\mathscr{P}\subseteq \mathbb{Z}$
, and for every
$\mathscr{P}\subseteq \mathbb{Z}$
, and for every
![]() $p\in \mathscr{P}$
, a subset
$p\in \mathscr{P}$
, a subset
![]() $\mathscr{D}_{p}\subseteq \text{Spec}A$
satisfying the following conditions.
$\mathscr{D}_{p}\subseteq \text{Spec}A$
satisfying the following conditions.
-
(1)
 $\mathscr{D}_{p}$
is a dense subset of
$\mathscr{D}_{p}$
is a dense subset of
 $\unicode[STIX]{x1D70B}^{-1}(p)$
, where
$\unicode[STIX]{x1D70B}^{-1}(p)$
, where
 $\text{Spec}A\stackrel{\unicode[STIX]{x1D70B}}{\longrightarrow }\text{Spec}\mathbb{Z}$
.
$\text{Spec}A\stackrel{\unicode[STIX]{x1D70B}}{\longrightarrow }\text{Spec}\mathbb{Z}$
. -
(2)
 $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\min \left\{1,\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}}})\right\}$
for every maximal ideal
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\min \left\{1,\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}}})\right\}$
for every maximal ideal
 $\unicode[STIX]{x1D707}\in \mathscr{D}_{p}$
.
$\unicode[STIX]{x1D707}\in \mathscr{D}_{p}$
.
Proof. Let
![]() $\mathscr{D}=\bigcup _{p\in \mathscr{P}}\mathscr{D}_{p}$
. As
$\mathscr{D}=\bigcup _{p\in \mathscr{P}}\mathscr{D}_{p}$
. As
![]() $\mathscr{D}_{p}$
is dense in
$\mathscr{D}_{p}$
is dense in
![]() $\unicode[STIX]{x1D70B}^{-1}(p)$
,
$\unicode[STIX]{x1D70B}^{-1}(p)$
,
![]() $\overline{\mathscr{D}_{p}}=\unicode[STIX]{x1D70B}^{-1}(p)$
, and thus
$\overline{\mathscr{D}_{p}}=\unicode[STIX]{x1D70B}^{-1}(p)$
, and thus
By Corollary 49,
![]() $\unicode[STIX]{x1D70B}^{-1}(\mathscr{P})$
is dense in
$\unicode[STIX]{x1D70B}^{-1}(\mathscr{P})$
is dense in
![]() $\text{Spec}A$
, and (6.2) then shows that
$\text{Spec}A$
, and (6.2) then shows that
![]() $\mathscr{D}$
is dense as well. Let
$\mathscr{D}$
is dense as well. Let
![]() $U\subseteq \text{Spec}A$
be the dense open set given by Theorem 51. As
$U\subseteq \text{Spec}A$
be the dense open set given by Theorem 51. As
![]() $\mathscr{D}$
is dense and
$\mathscr{D}$
is dense and
![]() $U$
is dense and open, it follows that
$U$
is dense and open, it follows that
![]() $U\cap \mathscr{D}$
is dense in
$U\cap \mathscr{D}$
is dense in
![]() $\text{Spec}A$
. Furthermore, for
$\text{Spec}A$
. Furthermore, for
![]() $\unicode[STIX]{x1D707}\in U\cap \mathscr{D}$
,
$\unicode[STIX]{x1D707}\in U\cap \mathscr{D}$
,
Indeed, the leftmost inequality in (6.3) holds by Proposition 45, the first equality by Corollary 46, the second equality by our assumption on
![]() $\mathscr{D}$
, and the rightmost inequality by the defining property of
$\mathscr{D}$
, and the rightmost inequality by the defining property of
![]() $U$
. We conclude from (6.3) that
$U$
. We conclude from (6.3) that
![]() $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)$
for every maximal ideal
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}})=\mathbf{lct}(f)$
for every maximal ideal
![]() $\unicode[STIX]{x1D707}$
in the dense subset
$\unicode[STIX]{x1D707}$
in the dense subset
![]() $U\cap \mathscr{D}$
of
$U\cap \mathscr{D}$
of
![]() $\text{Spec}A$
, and the claim follows.◻
$\text{Spec}A$
, and the claim follows.◻
Theorem 58. Let
![]() $f\in \mathbb{C}[x_{1},\ldots ,x_{m}]$
be a polynomial vanishing at the origin. Fix distinct, nonzero vectors
$f\in \mathbb{C}[x_{1},\ldots ,x_{m}]$
be a polynomial vanishing at the origin. Fix distinct, nonzero vectors
![]() $\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}$
in
$\mathbf{a}_{1},\ldots ,\mathbf{a}_{n}$
in
![]() $\mathbb{N}^{m}$
, and elements
$\mathbb{N}^{m}$
, and elements
![]() $u_{1},\ldots ,u_{n}$
in
$u_{1},\ldots ,u_{n}$
in
![]() $\mathbb{C}^{\ast }$
, such that
$\mathbb{C}^{\ast }$
, such that
![]() $f=\sum _{i=1}^{n}u_{i}x^{\mathbf{a}_{i}}$
. If the coefficients
$f=\sum _{i=1}^{n}u_{i}x^{\mathbf{a}_{i}}$
. If the coefficients
![]() $u_{1},\ldots ,u_{n}$
form an algebraically independent sequence over
$u_{1},\ldots ,u_{n}$
form an algebraically independent sequence over
![]() $\mathbb{Q}$
, then log canonicity equals dense
$\mathbb{Q}$
, then log canonicity equals dense
![]() $F$
-pure type for
$F$
-pure type for
![]() $f$
.
$f$
.
Proof. By hypothesis,
![]() $\mathbb{Z}[u_{1},\ldots ,u_{n}]$
is a polynomial ring, with each
$\mathbb{Z}[u_{1},\ldots ,u_{n}]$
is a polynomial ring, with each
![]() $u_{i}$
a variable. If we set
$u_{i}$
a variable. If we set
![]() $A:=\mathbb{Z}[u_{1},\ldots ,u_{n}]_{\prod u_{i}}\subseteq \mathbb{C}$
, then
$A:=\mathbb{Z}[u_{1},\ldots ,u_{n}]_{\prod u_{i}}\subseteq \mathbb{C}$
, then
![]() $f\in S_{A}$
, and
$f\in S_{A}$
, and
![]() $\text{Supp}(f_{\unicode[STIX]{x1D707}})=\text{Supp}(f)$
for all maximal ideals
$\text{Supp}(f_{\unicode[STIX]{x1D707}})=\text{Supp}(f)$
for all maximal ideals
![]() $\unicode[STIX]{x1D707}\subseteq A$
. Set
$\unicode[STIX]{x1D707}\subseteq A$
. Set
![]() $\unicode[STIX]{x1D6FE}=\min \left\{1,\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}}})\right\}$
, and fix
$\unicode[STIX]{x1D6FE}=\min \left\{1,\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}}})\right\}$
, and fix
![]() $\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}\cap \mathbb{Q}^{m}$
(such points exist, as
$\boldsymbol{\unicode[STIX]{x1D702}}\in \mathbf{P}_{\text{max}}\cap \mathbb{Q}^{m}$
(such points exist, as
![]() $\mathbf{P}$
is rational, and
$\mathbf{P}$
is rational, and
![]() $\mathbf{P}_{\text{max}}$
is a face of
$\mathbf{P}_{\text{max}}$
is a face of
![]() $\mathbf{P}$
). If
$\mathbf{P}$
). If
![]() $\boldsymbol{\unicode[STIX]{x1D706}}:=\frac{\unicode[STIX]{x1D6FE}}{|\boldsymbol{\unicode[STIX]{x1D702}}|}\cdot \boldsymbol{\unicode[STIX]{x1D702}}$
, it follows that
$\boldsymbol{\unicode[STIX]{x1D706}}:=\frac{\unicode[STIX]{x1D6FE}}{|\boldsymbol{\unicode[STIX]{x1D702}}|}\cdot \boldsymbol{\unicode[STIX]{x1D702}}$
, it follows that
![]() $\boldsymbol{\unicode[STIX]{x1D706}}\in P\cap \mathbb{Q}^{m}$
(indeed, it lies in the line segment connecting
$\boldsymbol{\unicode[STIX]{x1D706}}\in P\cap \mathbb{Q}^{m}$
(indeed, it lies in the line segment connecting
![]() $\mathbf{0}$
and
$\mathbf{0}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D702}}$
), and satisfies
$\boldsymbol{\unicode[STIX]{x1D702}}$
), and satisfies
![]() $|\boldsymbol{\unicode[STIX]{x1D706}}|=\unicode[STIX]{x1D6FE}$
. If
$|\boldsymbol{\unicode[STIX]{x1D706}}|=\unicode[STIX]{x1D6FE}$
. If
![]() $\mathscr{P}$
denotes the set of primes
$\mathscr{P}$
denotes the set of primes
![]() $p$
such that
$p$
such that
![]() $(p-1)\cdot \boldsymbol{\unicode[STIX]{x1D706}}\in \mathbb{N}^{n}$
, then
$(p-1)\cdot \boldsymbol{\unicode[STIX]{x1D706}}\in \mathbb{N}^{n}$
, then
![]() $^{\#}\mathscr{P}=\infty$
by Dirichlet’s theorem on primes in arithmetic progressions. Fix a prime
$^{\#}\mathscr{P}=\infty$
by Dirichlet’s theorem on primes in arithmetic progressions. Fix a prime
![]() $p\in \mathscr{P}$
. It follows from the multinomial theorem that
$p\in \mathscr{P}$
. It follows from the multinomial theorem that
![]() $x^{(p-1)\mathbf{E}\boldsymbol{\unicode[STIX]{x1D706}}}$
appears in
$x^{(p-1)\mathbf{E}\boldsymbol{\unicode[STIX]{x1D706}}}$
appears in
![]() $f^{(p-1)\unicode[STIX]{x1D6FE}}$
with coefficient
$f^{(p-1)\unicode[STIX]{x1D6FE}}$
with coefficient
where the sum extends over all
![]() $\mathbf{k}\in \mathbb{N}^{n}$
such that
$\mathbf{k}\in \mathbb{N}^{n}$
such that
![]() $|\mathbf{k}|=(p-1)\unicode[STIX]{x1D6FE}$
, and
$|\mathbf{k}|=(p-1)\unicode[STIX]{x1D6FE}$
, and
![]() $\mathbf{E}\mathbf{k}=(p-1)\cdot \mathbf{E}\boldsymbol{\unicode[STIX]{x1D706}}$
. As
$\mathbf{E}\mathbf{k}=(p-1)\cdot \mathbf{E}\boldsymbol{\unicode[STIX]{x1D706}}$
. As
![]() $(p-1)\cdot \boldsymbol{\unicode[STIX]{x1D706}}$
is such an index, it follows that
$(p-1)\cdot \boldsymbol{\unicode[STIX]{x1D706}}$
is such an index, it follows that
![]() $\unicode[STIX]{x1D6E9}_{\boldsymbol{\unicode[STIX]{x1D706}},p}(u_{1},\ldots ,u_{n})$
defines a nonzero element of the polynomial ring
$\unicode[STIX]{x1D6E9}_{\boldsymbol{\unicode[STIX]{x1D706}},p}(u_{1},\ldots ,u_{n})$
defines a nonzero element of the polynomial ring
![]() $\mathbb{Z}[u_{1},\ldots ,u_{n}]$
. Moreover, as
$\mathbb{Z}[u_{1},\ldots ,u_{n}]$
. Moreover, as
![]() $\unicode[STIX]{x1D6FE}\leqslant 1$
,
$\unicode[STIX]{x1D6FE}\leqslant 1$
,
![]() $\binom{(p-1)\cdot \unicode[STIX]{x1D6FE}}{\mathbf{k}}\neq 0~\text{mod}~p$
for each
$\binom{(p-1)\cdot \unicode[STIX]{x1D6FE}}{\mathbf{k}}\neq 0~\text{mod}~p$
for each
![]() $\mathbf{k}$
in (6.4), and it follows that the image of
$\mathbf{k}$
in (6.4), and it follows that the image of
![]() $\unicode[STIX]{x1D6E9}_{\boldsymbol{\unicode[STIX]{x1D706}},p}(u_{1},\ldots ,u_{n})$
defines a nonzero element of the polynomial ring
$\unicode[STIX]{x1D6E9}_{\boldsymbol{\unicode[STIX]{x1D706}},p}(u_{1},\ldots ,u_{n})$
defines a nonzero element of the polynomial ring
![]() $\mathbb{Z}/p\mathbb{Z}[u_{1},\ldots ,u_{n}]\subseteq A/pA$
. Consider the map
$\mathbb{Z}/p\mathbb{Z}[u_{1},\ldots ,u_{n}]\subseteq A/pA$
. Consider the map
![]() $\text{Spec}A\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }\text{Spec}\mathbb{Z}$
induced by the inclusion
$\text{Spec}A\stackrel{\unicode[STIX]{x1D70B}}{\rightarrow }\text{Spec}\mathbb{Z}$
induced by the inclusion
![]() $\mathbb{Z}\subseteq A$
. We have just shown that
$\mathbb{Z}\subseteq A$
. We have just shown that
![]() $\mathscr{D}_{p}:=D(\unicode[STIX]{x1D6E9}_{\boldsymbol{\unicode[STIX]{x1D706}},p}(\mathbf{u}))\cap \unicode[STIX]{x1D70B}^{-1}(p)$
is a dense (and, in fact, open) subset of the fiber
$\mathscr{D}_{p}:=D(\unicode[STIX]{x1D6E9}_{\boldsymbol{\unicode[STIX]{x1D706}},p}(\mathbf{u}))\cap \unicode[STIX]{x1D70B}^{-1}(p)$
is a dense (and, in fact, open) subset of the fiber
![]() $\unicode[STIX]{x1D70B}^{-1}(p)$
. Let
$\unicode[STIX]{x1D70B}^{-1}(p)$
. Let
![]() $\unicode[STIX]{x1D707}_{p}$
be a maximal ideal in
$\unicode[STIX]{x1D707}_{p}$
be a maximal ideal in
![]() $\mathscr{D}_{p}$
. By definition, the image of
$\mathscr{D}_{p}$
. By definition, the image of
![]() $\unicode[STIX]{x1D6E9}_{\boldsymbol{\unicode[STIX]{x1D706}},p}(\mathbf{u})$
is nonzero in
$\unicode[STIX]{x1D6E9}_{\boldsymbol{\unicode[STIX]{x1D706}},p}(\mathbf{u})$
is nonzero in
![]() $A/\unicode[STIX]{x1D707}_{p}$
, and (6.4) shows that
$A/\unicode[STIX]{x1D707}_{p}$
, and (6.4) shows that
![]() $\boldsymbol{x}^{(p-1)\mathbf{E}\boldsymbol{\unicode[STIX]{x1D706}}}$
is contained in
$\boldsymbol{x}^{(p-1)\mathbf{E}\boldsymbol{\unicode[STIX]{x1D706}}}$
is contained in
![]() $\text{Supp}((f_{\unicode[STIX]{x1D707}_{p}})^{(p-1)\unicode[STIX]{x1D6FE}})$
but not in
$\text{Supp}((f_{\unicode[STIX]{x1D707}_{p}})^{(p-1)\unicode[STIX]{x1D6FE}})$
but not in
![]() $\mathfrak{m}^{[p^{}]}$
(as
$\mathfrak{m}^{[p^{}]}$
(as
![]() $\boldsymbol{\unicode[STIX]{x1D706}}\in \mathbf{P}$
). Thus,
$\boldsymbol{\unicode[STIX]{x1D706}}\in \mathbf{P}$
). Thus,
![]() $(f_{\unicode[STIX]{x1D707}_{p}})^{(p-1)\unicode[STIX]{x1D6FE}}\notin \mathfrak{m}^{[p^{}]}$
, which allows us to apply Lemma 13 to
$(f_{\unicode[STIX]{x1D707}_{p}})^{(p-1)\unicode[STIX]{x1D6FE}}\notin \mathfrak{m}^{[p^{}]}$
, which allows us to apply Lemma 13 to
![]() $f_{\unicode[STIX]{x1D707}_{p}}\in S_{A}(\unicode[STIX]{x1D707}_{p})$
to conclude that
$f_{\unicode[STIX]{x1D707}_{p}}\in S_{A}(\unicode[STIX]{x1D707}_{p})$
to conclude that
![]() $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}_{p}})\geqslant \unicode[STIX]{x1D6FE}=\min \left\{1,\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}}})\right\}$
. By Remark 12, the opposite bound always holds, and we conclude that
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}_{p}})\geqslant \unicode[STIX]{x1D6FE}=\min \left\{1,\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}}})\right\}$
. By Remark 12, the opposite bound always holds, and we conclude that
![]() $\mathbf{fpt}(f_{\unicode[STIX]{x1D707}_{p}})=\min \{1,\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}_{p}}})\}$
for every
$\mathbf{fpt}(f_{\unicode[STIX]{x1D707}_{p}})=\min \{1,\mathbf{fpt}(\mathfrak{a}_{f_{\unicode[STIX]{x1D707}_{p}}})\}$
for every
![]() $p\in \mathscr{P}$
, and
$p\in \mathscr{P}$
, and
![]() $\unicode[STIX]{x1D707}_{p}\in \mathscr{D}_{p}$
. In conclusion, we see that
$\unicode[STIX]{x1D707}_{p}\in \mathscr{D}_{p}$
. In conclusion, we see that
![]() $A,\mathscr{P}$
, and
$A,\mathscr{P}$
, and
![]() $\mathscr{D}_{p}$
satisfy the conditions of Lemma 57, and so we are done.◻
$\mathscr{D}_{p}$
satisfy the conditions of Lemma 57, and so we are done.◻
Acknowledgments
Many of the results contained in this article appear in the author’s Ph.D. thesis, completed at the University of Michigan. The author would like to thank his advisor, Karen Smith, for her guidance during this project. The author would also like to thank Emily Witt, Karl Schwede, Mel Hochster, and Vic Reiner for their useful comments on earlier versions of this article.