Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-29T08:28:18.949Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounded realization of l-groups over global fields

Published online by Cambridge University Press:  22 January 2016

Wulf-Dieter Geyer  and
Moshe Jarden
Wulf-Dieter Geyer
Affiliation:
Mathematisches Institut, Universität Erlangen, Bismarckstraße 1½, 91054, Germany, geyer@mi.uni-erlangen.de
Moshe Jarden
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Ramat Aviv, Tel Aviv 69978, Israel, jarden@math.tau.ac.il
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use the method of Scholz and Reichardt and a transfer principle from finite fields to pseudo finite fields in order to prove the following result. THEOREM Let G be a group of order ln, where l is a prime number. Let K0be either a finite field with |K0| > l4n+4or a pseudo finite field. Suppose that l ≠ char(K0) and that K0does not contain the root of unity ζl of order l. Let K = K0(t), with t transcendental over K0. Then K has a Galois extension L with the following properties: (a) 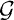(L/K) ≅ G; (b) L/K0is a regular extension; (c) genus(L) < 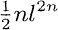; (d) K0[t] has exactly n prime ideals which ramify in L; the degree of each of them is [K0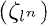: K0]; (e) (t)∞totally decomposes in L; (f) L = K(x), with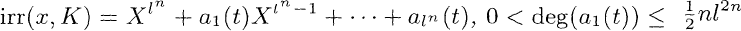and deg(ai(t)) < deg(a1(t)) for i = 1,…,ln.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 150 , June 1998 , pp. 13 - 62
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1998

References

[Ax] Ax, J., The elementary theory of finite fields, Annals of Mathematics, 88 (1968), 239–271.Google Scholar
[CaF] Cassels, J. W. S. and Fröhlich, A., Algebraic Number Theory, Academic Press, London, 1967.Google Scholar
[FrJ] Fried, M. D. and Jarden, M., Field Arithmetic, Ergebnisse der Mathematik (3), 11, Springer, Heidelberg (1986).Google Scholar
[FrV] Fried, M. D. and Völklein, H., The inverse Galois problem and rational points on moduli spaces, Mathematische Annalen 290 (1991), 771–800.Google Scholar
[GeJ] Geyer, W.-D. and Jensen, C. U., Extension prodiédrales, C. R. Acad. Sci. Paris Sér. I, 319 (1994), 1241–1244.Google Scholar
[HaV] Haran, D. and Völklein, H., Galois groups over complete valued fields, Isreal Journal of Mathematics, 93 (1996), 9–27.Google Scholar
[Hoe] Hoechsmann, Klaus, Zum Einbettungsproblem, Journal für die reine und ungewandte Mathematik, 229 (1968), 81–106.Google Scholar
[HKo] Halter-Koch, F., Der Čebotarev’sche Dichtigkeitsatz und ein analogon zum Dirichlet’chen Primzahlsatz für algebraische Funktionenkörper, manuscripta mathematica, 72 (1991), 205–211.Google Scholar
[Jal] Jarden, M., Elementary statements over large algebraic fields, Transactions of AMS, 164 (1972), 67–91.Google Scholar
[Ja2] Jarden, M., The inverse Galois problem over formal power series fields., Israel Journal of Mathematics, 85 (1994), 263–275.Google Scholar
[Koc] Koch, H., l-Erweiterungen mit vorgegebener Verzweigunsstellen, Journal für die reine und angewandte Mathematik, 219 (1965), 30–61.Google Scholar
[Lan] Lang, S., Algebra, Addison-Wesley, Reading, 1970.Google Scholar
[La2] Lang, S., Algebraic Number Theory, Addison-Wesley, Reading, 1970.Google Scholar
[La3] Lang, S., Introduction to algebraic geometry, Interscience Publishers, New York, 1958.Google Scholar
[La4] Lang, S., Algebra, Second Edition, Addison-Wesley, Menlo Park, 1984.Google Scholar
[Neu] Neukirch, J., Class field theory, Grundlehren der mathematischen Wissenschaften, 280 (1985), Springer, Berlin.Google Scholar
[RCV] Rzedowski-Calderón, and Villa-Salvador, , Automorphisms of congruence function fields, Pacific Journal of Mathematics, 150 (1991), 167–178.Google Scholar
[Rei] Reichardt, H., Konstruktion von Zahlkörpern mit gegebener Galoisgruppe von Primzahlpotenzordnung, Journal für die reine und angewandte Mathematik, 177 (1937), 1–5.Google Scholar
[Sch] Arnold, Scholz, Konstruktion algebraischer Zahlkörper mit beliebiger Gruppe von Primzahlpotenzordnung I, Mathematische Zeitschrift, 42 (1936), 161–188.Google Scholar
[Sel] Serre, J.-P., Topics in Galois Theory, Jones and Barlett, Boston, 1992.Google Scholar
[Se2] Serre, J.-P., Corps Locaux, Hermann, Paris, 1962.Google Scholar
[Sh1] Shafarevich, I. R., On the construction of fields with a given Galois group of order l a , Izv. Akad. Nauk, 18 (1954), 261–296, = Collected Mathematical Papers 69–97, Springer, Berlin, 1989.Google Scholar
[Sh2] Shafarevich, I. R., Factors of descending central series, Mathematical Notes, 45 (1989), 262–264.Google Scholar