Article contents
Algebras and differential equations
Published online by Cambridge University Press: 22 January 2016
Extract
One purpose of this paper is a purely algebraic study of (systems of) ordinary differential equations of the type
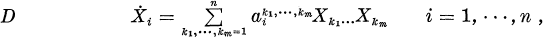
where the coefficients are taken from a fixed associative, commutative, unital ring R, such as the field R of real or C of complex numbers or a commutative, unital Banach algebra. The right hand sides of D are considered to be elements in the polynomial ring R[X1, …, Xn] of associating but non-commuting variables X1, …, Xn. An algebraic study calls for maps between such differential equations and, in fact, morphisms are defined between differential equations having the same arity m but not necessarily the same dimension n. These morphisms are rectangular matrices with entries in R which satisfy certain relations. This leads to a category RDiffm whose objects are precisely the differential equations of arity m and in which the composition of the morphisms is the usual matrix multiplication.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1977
References
- 16
- Cited by


