Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-24T14:13:43.283Z Has data issue: false hasContentIssue false
  • English
  • Français

Phase field modeling of intercalation kinetics: a finite interface dissipation approach

Published online by Cambridge University Press:  30 August 2016

Nega A. Zerihun  and
Ingo Steinbach
Nega A. Zerihun*
Affiliation:
Addis Ababa Institute of Technology, Center for Materials Engineering, King George IV Street, P.O. Box 385, Addis Ababa, Ethiopia
Ingo Steinbach
Affiliation:
Interdisciplinary Centre for Advanced Materials Simulation (ICAMS), Ruhr-Universität Bochum, IC 02-509, Universitätsstr. 150, 44801 Bochum, Germany
*
Address all correspondence to Nega A. Zerihun at nega.alemayehu@aait.edu.et or nega.alemayehu@rub.de
Get access

Abstract

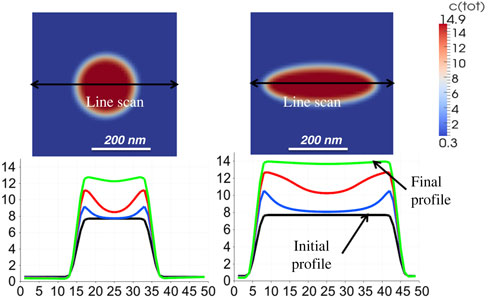
When two materials interact, the processes between the phases determine the functional properties of the compound. Pivotal interface phenomena are diffusion and redistribution of atoms (molecules). This is especially of interest in Lithium ion batteries where the interfacial kinetics determines the battery performance and impact cycling stability. A new phase field model, which links the atomistic processes at the interface to the mesoscale transport by a redistribution flux controlled by the so called ‘interface permeability’ was developed. The model was validated with experimental data from diffusion couples. Calculations of the concentration profiles of the species at the electrode–electrolyte interface are reported. Active particle size, morphology and spatial arrangement were put in correlation with diffusion behavior for use in reverse engineering.

Type
Prospective Article
Information
MRS Communications , Volume 6 , Issue 3 , September 2016 , pp. 270 - 282
Check for updates
Copyright
Copyright © Materials Research Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Whittingham, M.S.: Electrical energy storage and intercalation chemistry. Science 192, 1126–1127 (1976).Google Scholar
2. Boettinger, W.J., Warren, J.A., Beckermann, C., and Karma, A.: Phase field simulation of solidification. Ann. Rev. Mater. Res. 32, 163–194 (2002).Google Scholar
3. Chen, L.-Q.: Phase field models for microstructure evolution. Ann. Rev. Mater. Res. 32, 113–140 (2002).Google Scholar
4. Wang, S.L., Sekerka, R.F., Wheeler, A.A., Murray, B.T., Coriell, S.R., Braun, R.J., and McFadden, G.B.: Thermodynamically consistent phase field models for solidification. Physica D: Nonlinear Phenomena 69, 189–200 (1993).CrossRefGoogle Scholar
5. Steinbach, I.: Phase-field models in materials science. Model. Simul. Mater. Sci. Eng. 17, 073001 (2009).Google Scholar
6. Levitas, V.I. and Roy, A.M.: Multiphase phase field theory for temperature- and stress induced phase transformations. Phys. Rev. B 91, 174109 (2015).Google Scholar
7. Momeni, K. and Levitas, V.I.: A phase-field approach to nonequilibrium phase transformations in elastic solids via an intermediate phase (melt) allowing for interface stresses. Phys. Chem. Chem. Phys. 18, 12183–12203 (2016).CrossRefGoogle ScholarPubMed
8. Denoual, C. and Vattré, A.: A phase field approach with a reaction pathways-based potential to model reconstructive martensitic transformations with a large number of variants. J. Mech. Phys. Solids 90, 91–107 (2016).Google Scholar
9. Levitas, V.I. and Samani, K.: Size and mechanics effects in surface-induced melting of nanoparticles. Nat. Commun. 2, 284 (2011).Google Scholar
10. Momeni, K., Levitas, V.I., and Warren, J.A.: The strong influence of internal stresses on the nucleation of a nanosized, deeply undercooled melt at a solid–solid phase interface. Nano Lett. 15, 2298–2303 (2015).Google Scholar
11. Chen, L.-Q. and Yang, W.: Computer simulation of the domain dynamics of quenched system with a large number of nonconserved order parameters: the grain-growth kinetics. Phys. Rev. B 50, 15752 (1994).Google Scholar
12. Miyoshia, E. and Takaki, T.: Validation of a novel higher-order multi-phase-field model for grain-growth simulations using anisotropic grain-boundary properties. Comput. Mater. Sci. 112, 44–51 (2016).Google Scholar
13. Chen, L. and Hu, S.: Solute segregation and coherent nucleation and growth near a dislocation: a phase-field model integrating defect and phase microstructures. Acta Mater. 49, 463–472 (2001).Google Scholar
14. Rodney, D., Le Bouar, Y., and Finel, A.: Phase field methods and dislocations. Acta Mater. 51, 17–30 (2003).Google Scholar
15. Wang, L., Liu, Z. and Zhuang, Z.: Developing micro-scale crystal plasticity model based on phase field theory for modeling dislocations in heteroepitaxial structures. Int. J. Plasticity 81, 267–283 (2016).Google Scholar
16. Jin, Y., Wang, Y., and Khachaturyan, A.: Three-dimensional phase field microelasticity theory and modelling of multiple cracks and voids. Appl. Phys. Lett. 79, 3071 (2001).Google Scholar
17. Levine, H. and Henry, H.: Dynamic instabilities of fracture under biaxial strain using a phase field model. Phys. Rev. Lett. 93, 105504 (2004).Google Scholar
18. Patton, B., Kazaryan, A., and Wang, Y.: Generalized phase field approach for computer simulation of sintering: incorporation of rigid-body motion. Scripta Mater. 41, 487–492 (1999).Google Scholar
19. Jing, X.N., Zhao, J.H., Subhash, G., and Gao, X.L.: Anisotropic grain growth with pore drag under applied loads. Mater. Sci. Eng. A 412, 271–278 (2005).Google Scholar
20. Wang, Y.: Computer modeling and simulation of solid-state sintering: a phase field approach. Acta Mater. 54, 953–961 (2006).Google Scholar
21. Du, Q., Liu, C., and Wang, X.: Simulating the deformation of vesicle membranes under elastic bending energy in three dimensions. J. Comput. Phys. 212, 757–777 (2006).Google Scholar
22. Biben, T., Kassner, K., and Misbah, C.: Phase-field approach to three dimensional vesicle dynamics. Phys. Rev. E 72, 041921 (2005).Google Scholar
23. Guyer, J., Boettinger, W., Warren, J., and McFadden, G.: Phase field modeling of electrochemistry I: equilibrium. Phys. Rev. E 69, 021603 (2004).Google Scholar
24. Guyer, J., Boettinger, W., Warren, J., and McFadden, G.: Phase field modeling of electrochemistry II: kinetics. Phys. Rev. E 69, 021604 (2004).Google Scholar
25. Pongsaksawad, W., Powell, A.C., and Dussault, D.: Phase-field modeling of transport-limited electrolysis in solid and liquid states. J. Electrochem. Soc. 154, F122 (2007).CrossRefGoogle Scholar
26. Shibuta, Y., Okajima, Y., and Suzuki, T.: Phase field modeling for electrodeposition process. Sci. Technol. Adv. Mater. 8, 511–518 (2007).Google Scholar
27. Steinbach, I., Zhang, L., and Plapp, M.: Phase-field model with finite interface dissipation. Acta Mater. 60, 2689–2701 (2012).Google Scholar
28. Zhang, L. and Steinbach, I.: Phase-field model with finite interface dissipation: extension to multi-component multi-phase alloys. Acta Mater. Elsevier Ltd. 60, 2702–2710 (2012).Google Scholar
29. Preiss, U., Borukhovich, E., Alemayehu, N., and Steinbach, I.: A permeation model for the electrochemical interface. Model. Simul. Mater. Sci. Eng. 21, 4006 (2013).CrossRefGoogle Scholar
30. Steinbach, I. and Apel, M.: Phase-field simulation of rapid crystallization of silicon on substrate. Mater. Sci. Eng. A, Elsevier Sci. SA, Lausanne 449, 95–98 (2007).Google Scholar
31. Steinbach, I.: Phase field model for microstructure evolution at the mesoscopic scale. Ann. Rev. Mater. Res. 43, 89–107 (2013).Google Scholar
32. Tiaden, J., Nestler, B., Diepers, H.J., and Steinbach, I.: The multiphase-field model with an integrated concept for modelling solute diffusion. Physica D: Nonlinear Phenomena 115, 73–86 (1998).Google Scholar
33. Steinbach, I., Pezzolla, F., Nestler, B., Seesselberg, M., Prieler, R., Schmitz, G.J., and Rezende, J.L.L.: A phase field concept for multiphase systems. Physica D: Nonlinear Phenomena 94, 135–147 (1996).Google Scholar
34. Steinbach, I. and Pezzolla, F.: A generalized field method for multiphase transformations using interface fields. Physica D: Nonlinear Phenomena 134, 385–393 (1999).Google Scholar
35. Steinbach, I., Boetinger, B., Eiken, J., Warnken, N., and Fries, S.G.: CALPHAD and phase-field modeling: a successful Liaison. J. Phase Equilibria Diff. 28, 101–106 (2007).Google Scholar
36. Eiken, J., Boetiger, B., and Steinbach, I.: Multiphase-field approach for multicomponent alloys with extrapolation scheme for numerical application. Phys. Rev. E 73, 066122 (2006).Google Scholar
37. Boettinger, W.J. and Warren, J.A.: Simulation of the cell to plane front transition during directional solidification at high velocity. J. Cryst. Growth 200, 583–591 (1999).CrossRefGoogle Scholar
38. Gahn, J.W. and Baker, J.C.: Solute trapping by rapid solidification. Acta. Metall. 17, 575 (1969).Google Scholar
39. Kittl, J.A., Sanders, P.G., Aziz, M.J., Brunco, D.P., and Thompson, M.O.: Complete experimental test for kinetic models of rapid alloy solidification. Acta Mater. 48, 4797 (2000).Google Scholar
40. Wang, C.-W. and Sastry, A.M.: Mesoscale modeling of a Li-ion polymer cell. J. Electrochem. Soc. 154, A1035–A1047 (2007).Google Scholar
41. Singh, G.K., Ceder, G., and Bazant, M.Z.: Intercalation dynamics in rechargeable battery materials: General theory and phase transformation in LiFePO4 . Electrochim. Acta 53, 7599–7613 (2008).Google Scholar
42. Bazant, M.Z.: Theory of chemical kinetics and charge transfer based on nonequilibrium thermodynamics. Acc. Chem. Res. 46, 1144–1160 (2013).Google Scholar
43. Noel, V. and Rajendran, M.: A comprehensive model for cyclic voltammetric study of intercalation/de-intercalation. J. Power Sources 88, 243–249 (2000).Google Scholar
44. Flandrois, S.: Graphite intercalation compounds as electrode materials in batteries. Synth. Met. 4, 255 (1982).Google Scholar
45. Macdonald, J.R.: Impedance spectroscopy. Ann. Biomed. Eng. 20, 289–305 (1992).Google Scholar
46. Park, S.M. and Yoo, J.S.: Electrochemical impedance spectroscopy for better electro-chemical measurements. Anal. Chem. 75, 455A–461A (2003).Google Scholar
47. Lasia, A.: Electrochemical impedance spectroscopy and its applications. Modern Asp. Electrochem. 32, 143–248 (1999).Google Scholar
48. Wang, C. and Hong, J.: Ionic/electronic conducting characteristics of LiFePO4 cathode materials. Electrochem. Solid-State Lett. 10, A65–A69 (2007).Google Scholar
49. Vielstich, W., Hamann, C.H., and Hamnett, A.: Electrochemistry (Wiley-VCH, Weinheim, 2007).Google Scholar
50. Zhu, Y. and Wang, C.: Novel CV for phase transformation electrodes. J. Phys. Chem. C 115, 823–832 (2011).CrossRefGoogle Scholar
51. Katz, E. and Willner, I.: Probing biomolecular interactions at conductive and semi-conductive surfaces by impedance spectroscopy: routes to impedimetric immunosensors, DNA-sensors, and enzyme biosensors. Electroanalysis 15, 913–947 (2003).Google Scholar
52. Paolo, P., Lisi, M., Zane, D., and Pasquali, M.: Determination of the chemical diffusion coefficient of lithium in LiFePO4 . Solid State Ionics 148, 45–51 (2002).Google Scholar
53. Wang, S., Wang, Q., Liu, J., Cheng, Z., Si, D., and Geng, B.: Kinetic manipulation of the morphology evolution of FePO4 microcrystals: from rugbies to porous microspheres. Cryst. Eng. Commun. 11, 2510 (2009).Google Scholar
54. Ellis, B.L., Michael Makahnouk, W.R., Rowan-Weetaluktuk, W.N., Ryan, D.H., and Nazar, L.F.: Crystal structure and electrochemical properties of A2MPO4F fluorophosphates (A=Na, Li; M=Fe, Mn, Co, Ni). Chem. Mater. 22, 1059–1070 (2010).Google Scholar
55. Ellis, B.L., Lee, K.T., and Nazar, L.F.: Positive electrode materials for Li-ion and Li-batteries. Chem. Mater. 22, 691–714 (2010).Google Scholar
56. Malik, R., Burch, D., Bazant, M., and Ceder, G.: Particle size dependence of the ionic diffusivity. Nano Lett. 10, 4123–4127 (2010).Google Scholar
57. Sinha, N.N. and Munichandraiah, N.: The effect of particle size on performance of cathode materials of Li-ion batteries. J. Indian Inst. Sci. 89, 381–392 (2009).Google Scholar
58. Lee, K.T. and Cho, J.: Roles of nanosize in lithium reactive nanomaterials for lithium ion batteries. Nano Today 6, 28–41 (2011).Google Scholar
59. Kai, K., Kobayashi, Y., Miyashiro, H., Oyama, G., Nishimura, S., Okubo, M., and Yamada, A.: Particle-size effects on the entropy behavior of a Li x FePO4 electrode. Chem. Phys Chem 15, 2156–2161 (2014).Google Scholar
60. Dua, W., Gupta, A., Zhang, X., Sastry, A.M., and Shyy, W.: Effect of cycling rate, particle size and transport properties on lithium-ion cathode performance. Int. J. Heat Mass Transf. 53, 3552–3561 (2010).Google Scholar
61. Bloom, I., Cole, B.W., Sohn, J.J., Jones, S.A., Polzin, E.G., Battaglia, V.S., Henriksen, G.L., Motloch, C., Richardson, R., Unkelhaeuser, T., Ingersoll, D., and Case, H.L.: An accelerated calendar and cycle life study of Li-ion cells. J. Power Sources 101, 238–247 (2001).Google Scholar
62. Ramadass, P., Haran, B., White, R., and Popov, B.N.: Mathematical modeling of the capacity fades of Li-ion cells. J. Power Sources 123, 230–240 (2003).Google Scholar
63. Ramasamy, R.P., White, R.E., and Popov, B.N.: Calendar life performance of pouch lithium-ion cells. J. Power Sources 141, 298–306 (2005).Google Scholar
64. Abraham, D.P., Liu, J., Chen, C.H., Hyung, Y.E., Stoll, M., Elsen, N., MacLaren, S., Twesten, R., Haasch, R., Sammann, E., Petrov, I., Amine, K., and Henriksen, G.: Diagnosis of power fade mechanisms in high-power lithium-ion cells. J. Power Sources 119, 511–516 (2003).Google Scholar