Introduction
In modern mineralogy, crystal structure and end-member chemical formula are considered as the most important intrinsic properties of a mineral species (Nickel, Reference Nickel1995; Nickel and Grice, Reference Nickel and Grice1998; Hawthorne et al., Reference Hawthorne, Mills, Hatert and Rumsey2021). The complexity of chemical composition and crystal structure are therefore fundamental characteristics of minerals that have high relevance to the understanding of their stability, occurrence and evolution. The universal quantitative measures of structural and chemical complexity were proposed in Krivovichev (Reference Krivovichev2012, Reference Krivovichev and Charykova2013, Reference Krivovichev2014; Krivovichev et al., Reference Krivovichev2018) on the basis of Shannon information theory and have been recognised as useful parameters for the analysis of various mineralogical and crystal chemical phenomena, from crystal-structure classifications to metastable crystallisation and mineral evolution (Tambornino et al., Reference Tambornino, Sappl and Hoch2015; Christy et al., Reference Christy, Mills, Kampf, Housley, Thorne and Marty2016; Varn and Crutchfield, Reference Varn and Crutchfield2016; Plášil et al., Reference Plášil, Petříček and Majzlan2017; Plášil, Reference Plášil2018a, Reference Plášil2018b, Reference Plášil2018c; Ovchinnikov et al., Reference Ovchinnikov, Bobnar, Prots, Borrmann, Sichelschmidt, Grin and Höhn2018; Majzlan et al., Reference Majzlan, Dachs, Benisek, Plášil and Sejkora2018; Colmenero et al., Reference Colmenero, Plášil and Sejkora2019; Gurzhiy and Plášil, Reference Gurzhiy and Plášil2019; Gurzhiy et al., Reference Gurzhiy, Kuporev, Kovrugin, Murashko, Kasatkin and Plášil2019, Reference Gurzhiy, Kalashnikova, Kuporev and Plášil2021; Hornfeck, Reference Hornfeck2020; Bindi et al., Reference Bindi, Nespolo, Krivovichev, Chapuis and Biagioni2020; Majzlan, Reference Majzlan2020; Mugnaioli et al., Reference Mugnaioli, Bonaccorsi, Lanza, Elkaim, Diez-Gómez, Sobrados, Gemmi and Gregorkiewitz2020; Sabirov and Shepelevich, Reference Sabirov and Shepelevich2021; Kaußler and Kieslich, Reference Kaußler and Kieslich2021, etc.). The aim of this review is to summarise the recent findings in the field of structural and chemical complexity of minerals and to outline possible directions for its further development. This work can be considered as a sequel for the previous review by Krivovichev (Reference Krivovichev2013) that was devoted to the modern introduction of information-based complexity measures into mineralogy (from a historical point of view, the pioneering contributions were made by Petrov (Reference Petrov1970), Bulkin (Reference Bulkin1972a, Reference Bulkin1972b) and Yushkin (Reference Yushkin1977)). Krivovichev (Reference Krivovichev2013) pointed out the importance of quantitative expression of structural and chemical complexity of minerals for mineralogy and the novel insights that may be deduced from complexity considerations. In this review, our analysis will be based upon a comprehensively updated and corrected database of information-based complexity measures of minerals (see Supplementary Information), some of which have been incorporated into the Global Earth Mineral Inventory (GEMI) database (Prabhu et al., Reference Prabhu, Morrison, Eleish, Zhong, Huang, Golden, Perry, Hummer, Ralph, Runyon, Fontaine, Krivovichev, Downs, Hazen and Fox2021).
The review is organised as follows. First, we discuss basic methodological principles of complexity analysis of minerals and provide an overview of theoretical developments, including extension of complexity measures, quantification and visualisation of different factors that contribute to the overall structural complexity of a mineral, and theoretical relations between complexity and configurational entropy. The second and third parts are based upon the analysis of an updated database of complexity parameters, including average complexities for different sets of minerals, and a review of the most complex minerals based upon the recent mineralogical discoveries. The relations between symmetry and complexity are discussed in the fourth part of the review, along with some interesting (though not completely unexpected) insights into the history of explorative mineralogical research. The applications of the complexity considerations in mineral evolution studies are described in the fifth section, whereas the sixth contains brief discussions of directions for further investigation.
Theory and methodology
Basic principles
In accord with the previous theoretical considerations (Krivovichev, Reference Krivovichev2012, Reference Krivovichev2013), the structural complexity is estimated as the amounts of structural Shannon information per atom (strI G) and per unit cell (strI G,total) calculated according to the following equations:
where k is the number of different crystallographic sites (crystallographic orbits) in the structure and pi is the random choice probability for an atom from the ith crystallographic orbit, that is:
where mi is a multiplicity of a crystallographic orbit (i.e. the number of atoms of a specific Wyckoff site in the reduced unit cell), and v is the total number of atoms in the reduced unit cell.
By analogy, the chemical complexity of a mineral can be estimated from its end-member formula extracted from the International Mineralogical Association List of Minerals (Pasero, Reference Pasero2021) and, in some cases, corrected by Krivovichev (Reference Krivovichev2021b). It should be emphasised that, within the context of this study, it is implicitly understood that each mineral has a unique end-member formula (Hawthorne et al., Reference Hawthorne, Mills, Hatert and Rumsey2021; Hawthorne, Reference Hawthorne2021). Thus, for the mineral with the end-member formula E(1)c 1E(2)c 2…E(k)ck, where E(i) is an ith chemical element in the formula and ci is its integer coefficient, the chemical information per atom (chemI G) and per formula unit, f.u. (chemI G,total) can be calculated as follows (Siidra et al., Reference Siidra, Zenko and Krivovichev2014; Krivovichev et al., Reference Krivovichev, Krivovichev and Hazen2018a, Reference Krivovichev, Charykova and Krivovichev2020a):
where k is the number of different elements in the formula and pi is the random-choice probability for an atom of the ith element, that is:
where ci is the coefficient of the ith element in the formula and e is the total number of atoms in the chemical formula:
Krivovichev et al. (Reference Krivovichev, Krivovichev and Hazen2018a) demonstrated that, on average, structural and chemical complexities correlate with each other, which agrees well with the intuitive feeling that chemically complex species generally possess complex crystal structures. Though there are exceptions of this empirical rule (Krivovichev, Reference Krivovichev2013), it is a statistically valid observation.
New developments: Hornfeck extension
In some cases, the information-based measures proposed by Krivovichev (Reference Krivovichev2012, Reference Krivovichev2013) do not possess enough discriminative power to distinguish between the crystal structures that are thought to be different in terms of their symmetry or thermodynamic stability. For instance, α- and β-quartz have the same structural complexity parameters, 0.918 bits/atom and 8.265 bits/cell, which is counter-intuitive, as the α → β transition is associated with the increase of symmetry from trigonal to hexagonal. In order to overcome these difficulties, Hornfeck (Reference Hornfeck2020) proposed to extend the information-based complexity measures by introducing chemical, combinatorial and coordinational parameters. In the framework of the Hornfeck's approach, the complexity parameters strI G and strI G,total defined by equations (1) and (2), respectively, are classified as combinatorial. The coordinational measures are defined as follows (in order to be consistent with the definitions given above, the Hornfeck notations of complexity measures are modified).
Each crystallographic (Wyckoff) site in a crystal structure has a finite number of degrees of freedom depending upon its site symmetry. For instance, the site located on the inversion centre has zero degrees of freedom, whereas one located on the mirror plane has two degrees of freedom. The number of degrees is called by Hornfeck (Reference Hornfeck2020) an arity, by analogy with mathematics, where arity means the number of arguments taken by a function. The arity may be equal to 0, 1, 2, and 3. Let the arity of the ith crystallographic site be denoted as ai. Then
is the sum of arities for a crystal structure consisting of k crystallographic orbits (k different Wyckoff sites). The information amount of the distribution of arities in the crystal structure is defined as (d.f. = degree of freedom)
where
For instance, for α-quartz (space group P3221), a 1(Si) = 1 (the Si atom is located on the twofold axis) and a 2(O) = 3 (general site). Therefore, A = 4, IA = 0.811 bits/d.f., IA,total = 3.245 bits/cell. In contrast, for β-quartz (space group P6222), a 1(Si) = 0, a 2(O) = 1 (general site), A = 1, IA = 0.000bits/d.f., IA,total = 0.000 bits/cell (Banaru et al., Reference Banaru, Aksenov and Krivovichev2021).
The IA and IA,total parameters are identified by Hornfeck (Reference Hornfeck2020) as coordinational complexity. The configurational complexity IGA can be calculated as a combination of combinatorial and coordinational complexities via the formulas:
where
The dimension of the IGA parameters is in bits per degree of freedom per atom (bits/d.f.; each atom is considered as an additional degree of freedom). The total configurational information amount per reduced unit cell is calculated as
The application of the equations (9 to 14) to α- and β-quartz results in different configurational complexities, 1.775 and 1.296 bits/d.f., respectively, and 15.978 and 12.955 bits/cell, respectively. The relative configurational simplicity of β-quartz corresponds to its thermodynamic nature of a high-temperature polymorph (see below).
The analogous calculations for sillimanite and andalusite that, otherwise, have the same structural complexity (Krivovichev, Reference Krivovichev2013) provide the values of 3.564 bits/d.f. and 160.366 bits/cell, and 3.638 bits/d.f. and 167.350 bits/cell, respectively. The lower complexity of sillimanite agrees well with its nature as a high-temperature Al2SiO5 polymorph.
Hornfeck (Reference Hornfeck2020) also provided measures for the chemical complexities of crystalline compounds based upon the atomic numbers of their constituent elements. Combined with combinatorial and coordinational complexities, the Hornfeck chemical complexity parameters provide a measure for a crystallographic complexity. The latter may be considered as numerical characteristics of crystalline compounds, and therefore is of use for digital crystal-structure classification purposes. In this review, however, we use the structural and chemical complexity parameters as defined by Krivovichev (Reference Krivovichev2013) and Krivovichev et al. (Reference Krivovichev, Krivovichev and Hazen2018a), respectively.
Complexity, configurational entropy, and entropy of mixing
The configurational entropy of crystalline solids has received considerable attention recently due to the development of high-entropy materials (see: Miracle and Senkov (Reference Miracle and Senkov2017), McCormack and Navrotsky (Reference McCormack and Navrotsky2021), Dippo and Vecchio (Reference Dippo and Vecchio2021), and references therein). In all cases, the authors refer to configurational entropy as to the entropy of mixing, in conformity with geochemical and mineralogical textbooks (Putnis, Reference Putnis1992; Ottonello, Reference Ottonello2000). However, it is evident that the configurational entropy as an entropy of an atomic configuration is not restricted to mixing entropy only, as a complex crystal structure with many crystallographic orbits (= many different Wyckoff sites) should obviously have lower configuration entropies compared to the isochemical structure with few crystallographic orbits. Thus, it makes sense to separate configurational entropy (S cfg) into configurational entropy sensu stricto (S cfg,ss) and configurational entropy of mixing (S cfg,mix):
In the case of ideal mixing and a ‘single-lattice model’ (i.e. when the solid consists of one lattice or one crystallographic orbit), the value of S cfg,mix is calculated as follows:
where R is a gas constant (~8.3145 J⋅K–1⋅mol–1), N is the number of different chemical elements occupying the ‘lattice’ under consideration, and fj is the concentration of the jth element (note that vacancy can also be considered as an entropic species) so that
For the ‘sublattice-model’ (i.e. when the crystal structure consists of several ‘sublattices’ (= several crystallographic orbits), the formula (16) transforms into (Miracle and Senkov, Reference Miracle and Senkov2017; Dippo and Vecchio, Reference Dippo and Vecchio2021):
where x is the number of ‘sublattices’ (= the number k of crystallographic orbits in our notations above), and ax is the number of sites in the xth ‘sublattice’ (= multiplicity mi of an ith crystallographic orbit relative to reduced unit cell).
Taking into account that ax = mi and x = k and applying the equation (3), the formula (18) transforms into:
According to the value of S cfg,mix, materials with structural disorder are classified into low-entropy (S cfg,mix < 1R), medium-entropy (1R < S cfg,mix < 1.5R), and high-entropy (S cfg,mix > 1.5R) materials (Dippo and Vecchio, Reference Dippo and Vecchio2021).
In order to derive the expression for the estimates of configurational entropy sensu stricto (i.e. the entropy associated with structural complexity, assuming that more complex structures have lower entropies), Krivovichev (Reference Krivovichev2016) suggested the following reasoning. The entropy is defined as
where k B is the Boltzmann constant (~1.38064⋅1023 J⋅K–1) and W is the number of microstates that realise the given macrostate. For the crystal structure consisting of one crystallographic orbit, the S cfg,ss is maximal with atomic entropy equal to
where N is the number of atoms that may exchange their positions locally at a given temperature (Krivovichev (Reference Krivovichev2016) assumed that this value is specific for a particular compound; the exchange of positions implies realisation of different microstates and the difference of atoms of the same element and the same crystallographic orbit). For the molar entropy, the equation (21) transforms into
Let us now suppose that, due to an unspecified reason, the symmetry of the initial crystal structure is reduced, and the single crystallographic orbit splits into k crystallographic orbits. Obviously, the crystal structure becomes more complex and its configurational entropy sensu stricto should decrease. Krivovichev (Reference Krivovichev2016) demonstrated that the amount by which the maximal value S cfg,ssmax is decreased, ΔS cfg,ss, is expressed as the following:
Then the configuration entropy sensu stricto of the resulting low-symmetry structure, S cfg,ss, can be calculated as
Through the combination of equations (1), (15), (19) and (24), one deduces that
or
where
is a new measure of structural complexity that takes into account contributions from complexity sensu stricto and structural disorder that by definition decreases structural complexity. Equation (27) provides a procedure to account for the influence of chemical substitutions and vacancies upon the overall structural complexity, and the parameter strIG ,mix can therefore be considered as a measure of crystal chemical complexity (or the degree of atomic order) that takes into account not only structural architecture, but also its chemical nature. As many important rock-forming minerals are complex solid solutions and can be considered as low-, medium- or high-entropy materials (McCormack and Navrotsky, Reference McCormack and Navrotsky2021), this measure might be useful for mineralogical and geochemical implications.
Equation (27) can be re-written as

where
is a contribution of mixing to the overall crystal-chemical complexity. It is obvious that, as strIG ≥ 0 and I mix ≥ 0, the case is possible when strIG < I mix and strIG ,mix < 0. This means that, in contrast to the measure of structural complexity strIG, the parameter of crystal chemical complexity may be negative and provide a positive contribution to the total configurational entropy of a crystalline solid.
Kaußler and Kieslich (Reference Kaußler and Kieslich2021) recently suggested the following method to calculate the atomic structural complexity parameter (denoted here as KKIG) in order to account for the presence of chemical substitutions (or partially occupied sites) in a crystal structure:
where fj is the occupancy of the ith site by jth element.
Taking into account that, for a given site,
one may re-group the equation (30) to get
or
Through the comparison of equation (33) with equation (28), it is clear that the application of the formula (30) to solid solutions leads to the results exactly opposite to those provided by the formula (27). According to eq. (30), the presence of chemical substitutions (including substitutions by vacancies) results in an increase of the overall structural complexity, i.e. the increase in the atomic order, which is counter-intuitive, as disorder decreases the degree of order (= structural complexity). In order to show this, let us consider the forsterite–fayalite solid solution, Mg2SiO4–Fe2SiO4. The crystal structure of forsterite–fayalite (space group Pbnm) contains two M sites (4a and 4c), one Si site (4c) and three O sites (4c, 4c and 8d). For the sake of convenience, we suppose that, in the Mg2SiO4–Fe2SiO4 solid solution, Fe distributes equally between two M sites. The application of the formulae (1) and (2) provides strIG = 2.522. The application of the formulae (29) and (28) provides for the composition Mg2(1–x)Fe2xSiO4:
In contrast, equation (30) provides:
Graphs corresponding to the behaviour of structural complexity indices versus the content x (the average Fe content in the M sites) are shown in Fig. 1. The value x = 0.5 corresponds to the state of maximal disorder (minimal degree of order) and has the minimal value of strIG ,mix, which agrees with general understanding of relations between order and complexity, whereas the KKIG value is maximal for x = 0.5, which contradicts those relations.

Fig. 1. Atomic structural complexities calculated using different approaches versus x value for the fayalite–forsterite Mg2(1–x)Fe2xSiO4 solid solution.
The value of strIG ,mix allows one to distinguish mineral species that have the same space group, similar unit-cell parameters, and differ in the degree of disorder only. Sanidine (Sa), orthoclase (Or) and microcline are the polymorphs of KAlSi3O8 with a different degree of Al–Si order at the tetrahedral sites. According to the current nomenclature (see, e.g. Krivovichev, Reference Krivovichev2020a), in K feldspars, Al preferentially occurs at the T1 site. If x Al(T1) is the content of Al at the T1 site, then x Al(T1) = 0.5 for orthoclase and 0.25 for sanidine (in microcline, all Al is at the T10 site with x = 1). The behaviour of strIG ,mix and entropy of mixing versus x Al(T1) is shown in Fig. 2. The crystal chemical complexity (= the degree of order) decreases with the increasing entropy of mixing.

Fig. 2. The behaviour of strIG ,mix and entropy of mixing versus the x Al(T1) content of Al at the T1 site for the orthoclase (Or) – sanidine (Sa) solid solution.
Ladder diagrams
The complexity of a crystal structure is a sum of contributions of different factors. In order to estimate quantitatively the amount of information generated by a particular structural element, Krivovichev (Reference Krivovichev2018) suggested the use of ladder diagrams for visualising different information amounts arising from specific levels of hierarchical organisation of a crystal structure. For oxysalt minerals in particular, the following levels can be recognised: (1) topological information (TI) reflecting the amount of information with respect to the topological structure of basic structural units (clusters, chains, ribbons, layers and frameworks); (2) structural information (SI) arising from the symmetry reduction of structural units due to their distortions induced by their interactions with their local environments (in some cases, structural information equals topological information); (3) packing information (PI) due to the appearance of several identical structural units in the reduced unit cell (for example, the cell may contain two identical layers that may or may not be symmetrically related); (4) information arising from the interstitial structure (IS) except for H atoms; and (5) information due to the presence of H atoms responsible for the formation of a hydrogen bonding (HB) system. The calculation of different contributions proceeds via sequential calculations starting from the determination of the highest symmetry of structural units present in the structure. This first step is probably the most challenging and corresponds to finding the highest symmetry embedding of the chemical bonding net in 3D Euclidean space. In principle, it can be generated by the Systre software program (Delgado-Friedrichs et al., Reference Delgado-Friedrichs, Hyde, O'Keeffe and Yaghi2017). To find the most symmetric embedding of a net, the algorithm of Systre software uses barycentric placement in which each vertex of the net is placed into the centre of gravity of its adjacent vertices (all vertices have the same weight). The resulting net is called stable if no two vertices collide. Stable nets have the maximal achievable crystallographic symmetry (Delgado-Friedrichs and O'Keeffe, Reference Delgado-Friedrichs and O'Keeffe2003). In many cases, the situation does not need application of Systre software, as the highest symmetry embedding may be determined from analysis of the topological structure of structural units by visual inspection. Figure 3 shows ladder diagrams for the four CaAl2Si2O8 polymorphs: anorthite (space group P $\bar{1}$![]() ), high-pressure or high-temperature anorthite (space group I $\bar{1}$
), high-pressure or high-temperature anorthite (space group I $\bar{1}$![]() ), dmisteinbergite and svyatoslavite (Krivovichev, Reference Krivovichev2020a). Both room- and high-temperature anorthites are based upon the feldspar-type tetrahedral framework, which is rather low in complexity (blue colour). The major contribution to the structural complexity is due to the distortion of the tetrahedral framework induced by its interaction to the interstitial Ca2+ cations (green colour). The specific contribution of Ca2+ cations is quite small (yellow colour). The tetrahedral networks in svyatoslavite and dmisteinbergite are topologically simpler than the feldspar framework, which is typical for metastable polymorphs (see below).
), dmisteinbergite and svyatoslavite (Krivovichev, Reference Krivovichev2020a). Both room- and high-temperature anorthites are based upon the feldspar-type tetrahedral framework, which is rather low in complexity (blue colour). The major contribution to the structural complexity is due to the distortion of the tetrahedral framework induced by its interaction to the interstitial Ca2+ cations (green colour). The specific contribution of Ca2+ cations is quite small (yellow colour). The tetrahedral networks in svyatoslavite and dmisteinbergite are topologically simpler than the feldspar framework, which is typical for metastable polymorphs (see below).

Fig. 3. The ladder diagrams for the Ca[Al2Si2O8] polymorphs with tetrahedron topologies: 1 – anorthite I $\bar{1}$![]() ; 2 – anorthite P $\bar{1}$
; 2 – anorthite P $\bar{1}$![]() ; 3 – dmisteinbergite; 4 – svyatoslavite. After Krivovichev (Reference Krivovichev, Charykova and Krivovichev2020a).
; 3 – dmisteinbergite; 4 – svyatoslavite. After Krivovichev (Reference Krivovichev, Charykova and Krivovichev2020a).
For some interesting applications of ladder diagrams to the analysis of uranyl minerals and inorganic compounds see Gurzhiy and Plášil (Reference Gurzhiy and Plášil2019) and Gurzhiy et al. (Reference Gurzhiy, Kuporev, Kovrugin, Murashko, Kasatkin and Plášil2019 and Reference Gurzhiy, Kalashnikova, Kuporev and Plášil2021).
Database on structural and chemical complexity of minerals
The present review is based upon the updated database of structural and chemical complexity parameters of minerals calculated by means of the equations (1–7). For the crystal structures of hydrated minerals, where the positions of H atoms could not be determined, the H-correction procedure was used as first described by Pankova et al. (Reference Pankova, Gorelova, Krivovichev and Pekov2018a) through introduction of surrogate H sites with corresponding multiplicities. No positional disorder was taken into account. For the calculation of chemical complexities, the end-member mineral chemical formulae were used as approved by the International Mineralogical Association (IMA; Pasero, Reference Pasero2021). The structural complexity parameters for mineral species have recently been partially incorporated into the Global Earth Mineral Inventory (GEMI) online database (Prabhu et al., Reference Prabhu, Morrison, Eleish, Zhong, Huang, Golden, Perry, Hummer, Ralph, Runyon, Fontaine, Krivovichev, Downs, Hazen and Fox2021; see below).
Complexity statistics
Average complexity for all minerals
Krivovichev (Reference Krivovichev2013) provided the following average structural complexity values (arithmetic means) for the mineral kingdom: 3.23(2) bits per atom and 228(6) bits per reduced unit cell, which corresponds to the average 70.6 atoms per cell (based upon 3949 structure reports). For October 2021, the revised values (arithmetic means) are 3.54(2) bits/atom and 345(10) bits/cell, respectively, corresponding to the average of 97.5 atoms per cell (based upon 4443 structure reports). The difference between the 2013 and 2021 values is due to the H-correction of the 2013 database and a high number of very complex minerals that have been discovered since 2013 (in particular, polyoxometalates; see below). The average chemical complexities (arithmetic means) are 1.63(1) bits per atom and 63(1) bits per formula, which account for the average number of 38.7 atoms per formula (based upon 5455 chemical formulae). The latter value is rather high, keeping in mind that most rock-forming minerals are rather simple in their chemical compositions.
Complexity distributions
The distributions of atomic information amounts, chemIG and strIG, versus the number of mineral species (N) are shown in Fig. 4a and b, respectively. Both distributions fit the normal modes, with the goodness-of-fit R 2 values of 0.970 and 0.974, respectively. In contrast, the distributions of total complexities, chemIG,total and strIG,total, are heavily right-skewed (Fig. 5a and b, respectively) and correspond to log-normal distributions.

Fig. 4. Distributions of the atomic (a) chemical and (b) structural complexities versus the number of minerals (N).

Fig. 5. Distributions of the total (a) chemical and (b) structural complexities versus the number of minerals (N).
The N− chemIG,total and N− strIG,total can be described by the following exponential functions:
The distributions N− log(chemI G,total) and N − log(strI G,total) for the representative sampling of all minerals are symmetrical and fit the log-normal distribution with the goodness-of-fit R 2 values of 0.954 and 0.974, respectively.
For a log-normal distribution, the most precise method for estimating the parameters μ* and σ* of the statistical population relies on the log transformation. The mean and empirical standard deviation of the logarithms of the data are calculated and then back-transformed (Sachs Reference Sachs1997; Limpert et al., Reference Limpert, Stahel and Abbt2001) as follows:

where $\bar{X}^\ast$![]() is the geometric mean of the data; s* is back-transformed empirical standard deviation of the logarithms of the data.
is the geometric mean of the data; s* is back-transformed empirical standard deviation of the logarithms of the data.
The mean ($\bar{X}_{\rm log\it x_i}$![]() ) and empirical standard deviation $( \rm\sigma_{\rm log \it x_i}$
) and empirical standard deviation $( \rm\sigma_{\rm log \it x_i}$![]() ) of the logarithms of the data and their estimators ($\bar{X}^\ast$
) of the logarithms of the data and their estimators ($\bar{X}^\ast$![]() and s*) for all minerals are given in Table 1. Note that the geometric means are substantially lower than the arithmetic means given above.
and s*) for all minerals are given in Table 1. Note that the geometric means are substantially lower than the arithmetic means given above.
Table 1. Average chemical and structural complexities for minerals.*

* n – number of minerals taken into account; $\bar{X}$![]() = arithmetic mean; σ = standard deviation; ${\rm \sigma} _{\bar{X}}$
= arithmetic mean; σ = standard deviation; ${\rm \sigma} _{\bar{X}}$![]() = standard error of mean; $\bar{X}_{logx_i}$
= standard error of mean; $\bar{X}_{logx_i}$![]() = arithmetic mean; $\rm \sigma _{\rm log\it x_i}$
= arithmetic mean; $\rm \sigma _{\rm log\it x_i}$![]() = standard deviation; ${\rm \sigma}_{\bar{X}}$
= standard deviation; ${\rm \sigma}_{\bar{X}}$![]() = standard error of mean; $\bar{X}^\ast{ = } 10 ^\wedge \bar{X}_{\rm log \it x_i}$
= standard error of mean; $\bar{X}^\ast{ = } 10 ^\wedge \bar{X}_{\rm log \it x_i}$![]() ; $s^\ast{ = } 10 ^\wedge \rm \sigma _{\rm log\it x_i}$
; $s^\ast{ = } 10 ^\wedge \rm \sigma _{\rm log\it x_i}$![]() .
.
The log-normal character of the total structural and chemical complexity distributions is the result of the log-normal distributions of the numbers of atoms per reduced unit cell and per formula unit (Table 1).
Krivovichev (Reference Krivovichev2012, Reference Krivovichev2013) mentioned that the atomic structural complexity (strIG) is symmetry-sensitive, whereas the number of atoms per cell (v) is a size-sensitive parameter, while strIG,total combines both symmetry and size as two sides of complexity. In some sense, the strIG and v quantities can be considered as intensive and extensive parameters, respectively. The normal distribution of strIG seems to be quite natural and reflects the influence of many mutually unrelated parameters upon the symmetry of crystals. The nature of the log-normal distribution of the v value deserves special attention.
Log-normal distributions are of high importance in many areas of science (Limpert et al., Reference Limpert, Stahel and Abbt2001) and, in particular, are used to describe species abundance distributions (SADs) in ecology. According to this model, there are few species with high and low abundances and many with intermediate values. It is, however, unclear how the ecological models can be used to understand the behaviour of mineral systems, where mineral species do not compete for food, territory and other resources. A possible explanation for the log-normal distribution of the number of atoms per formula or per cell is the balance between the need to accommodate different elements in the same cell (most minerals contain from four to five different chemical elements (Krivovichev and Charykova, Reference Krivovichev and Charykova2013; Krivovichev et al., Reference Krivovichev, Charykova and Krivovichev2018b) and the tendency of the crystal structures to be as simple as possible.
Average complexity for mineral classes
Arithmetic means for chemical and structural complexities of different mineral classes are provided in Table 2. It can be seen that the O-free (anoxic) mineral species are both chemically and structurally simpler than the mineral species containing oxygen as a mineral-forming component. Among O-bearing species, oxides are the simplest (taking into account the large number of binary oxides with relative chemical simplicity), whereas sulfates and borates are the most complex. The latter observation is expected, as the majority of sulfates and borates crystallise at low temperatures and are very frequently hydrated. Next in complexity are silicates, arsenates and phosphates that have different modes of origin, including both low- and high-temperature environments.
Table 2. Average structural and chemical complexities for different mineral classes.*

* N = number of minerals taken into account; $\bar{X}$![]() = arithmetic mean; $\rm\sigma _{\bar{X}}$
= arithmetic mean; $\rm\sigma _{\bar{X}}$![]() = standard error of arithmetic mean.
= standard error of arithmetic mean.
The higher complexity of O-bearing minerals agrees well with the fact that a large number of them have a secondary origin and form at the expense of primary O-free minerals (e.g. during oxidation of sulfide mineral deposits; Krivovichev et al., Reference Krivovichev, Krivovichev and Charykova2019b, Reference Krivovichev, Krivovichev and Charykova2020b). The difference in complexity between anoxic and O-bearing minerals also plays a crucial role in the complexity changes during mineral evolution, i.e. with the formation of a large suite of complex oxysalt minerals as a result of the Great Oxidation Event (Hazen et al., Reference Hazen, Papineau, Bleeker, Downs, Ferry, McCoy, Sverjensky and Yang2008; see below).
Most complex minerals: an update
Twenty most complex minerals: the 2021 list
Krivovichev (Reference Krivovichev2013) provided the following list of twenty most structurally complex minerals known at the time (IG,total in bits per cell): paulingite-(Ca) (6767), fantappièite (5948), sacrofanite (5317), mendeleevite-(Ce) (3399), bouazzerite (3035), megacyclite (2951), vandendriesscheite (2835), giuseppettite (2723), stilpnomelane (2484), stavelotite-(La) (2411), rogermitchellite (2321), parsettensite (2310), apjohnite (2305), antigorite (m = 17 polysome) (2250), tounkite (2188), tschörtnerite (2132), farneseite (2094), kircherite (2053), bannisterite (2031) and mutinaite (2025). The updated 2021 list of twenty most structurally complex minerals is given in Table 3 (the difference between the 2013 and 2021 parameters for particular minerals is due to the fact that the 2013 data did not take into account contributions from H atoms). Only one representative of a given structure type is listed: for example, only one member of the voltaite group is given, whereas other mineral species isotypic to voltaite (Majzlan et al., Reference Majzlan, Schlicht, Wierzbicka-Wieczorek, Giester, Pöllmann, Brömme, Doyle, Buth and Bender Koch2013) are omitted; mendeleevite-(Nd) is omitted, etc. Only eight species from the 2013 list remain in the 2021 list. The main reason is the discoveries of seven very complex minerals since 2013 (ewingite, morrisonite, vanarsite, paddlewheelite, gauthierite, rowleyite and meerschautite), the crystal-structure solution of ilmajokite, and the inclusion of the previously neglected or H-corrected species (voltaite, alfredstelznerite, manitobaite, parsettensite and postite).
Table 3. Twenty most structurally complex minerals, their space groups and complexity characteristics.

References: (1) Olds et al. (Reference Olds, Plášil, Kampf, Simonetti, Sadergaski, Chen and Burns2017a); (2) Kampf et al. (Reference Kampf, Hughes, Nash and Marty2016); (3) Zolotarev et al. (Reference Zolotarev, Krivovichev, Cámara, Bindi, Zhitova, Hawthorne and Sokolova2020); (4) Gordon et al. (Reference Gordon, Samson and Kamb1966); (5) Cámara et al. (Reference Cámara, Bellatreccia, Della Ventura, Mottan, Bindi, Gunter and Sebastiani2010); (6) Brugger et al. (Reference Brugger, Meisser, Krivovichev, Armbruster and Favreau2007); (7) Olds et al. (Reference Olds, Plášil, Kampf, Dal Bo and Burns2018); (8) Effenberger et al. (Reference Effenberger, Giester, Krause and Bernhardt1998); (9) Burns, Reference Burns1997); (10) Sokolova et al. (Reference Sokolova, Hawthorne, Pautov, Agakhanov and Karpenko2011); (11) Cooper et al. (Reference Cooper, Hawthorne, Galliski and Márquez-Zavalía2010); (12) Olds et al. (Reference Olds, Plášil, Kampf, Škoda, Burns, Čejka, Bourgoin and Boulliard2017b); (13) Kampf et al. (Reference Kampf, Cooper, Nash, Cerling, Marty, Hummer, Celestian, Rose and Trebisky2017); (14) Biagioni et al. (Reference Biagioni, Moëlo, Orlandi and Stanley2016); (15) Mereiter, Reference Mereiter1972); (16) Guggenheim and Eggleton, Reference Guggenheim and Eggleton1994); (17) Tait et al. (Reference Tait, Ercit, Abdu, Černý and Hawthorn2011); (18) Kampf et al. (Reference Kampf, Hughes, Marty and Nash2012); and (19) McDonald and Chao (Reference McDonald and Chao2010).
Ewingite, Mg8Ca8[(UO2)24(CO3)30O4(OH)12(H2O)8](H2O)130, is the Earth's most complex mineral reported so far with an estimated complexity of 23478 bits/cell. The mineral was found as golden-yellow crystals on a damp wall of the old Plavno mine of the Jáchymov ore district, western Bohemia, Czech Republic (Olds et al., Reference Olds, Plášil, Kampf, Simonetti, Sadergaski, Chen and Burns2017a), where it crystallised from low-temperature uranyl-bearing aqueous solutions. Its crystal structure contains a 54-nuclear (24U + 30C) uranyl carbonate cluster [(UO2)24(CO3)30O4(OH)12(H2O)8]32– shown in Fig. 6a. Its skeletal representation (Fig. 6b), where each node corresponds either to U (yellow) or to C (grey) centre emphasises the presence of four U3 triangles (with U–U distances shorter than 4 Å) that correspond to the trimers of three ((UO2)O5) pentagonal bipyramids sharing the same equatorial O atom. Two other building units are the [(UO2)(CO3)3] and [(UO2)(CO3)2(H2O)2] hexagonal bipyramids. The visual complexity of the cluster architecture can further be reduced by leaving only U atoms and the addition of the U–U links corresponding to the U–U distances in between 4 and 6.2 Å (Fig. 6c). The resulting graph can be considered as consisting of four U3 trimers (U–U < 4 Å) and six U4 dihedra of two edge-sharing U3 triangles (U–U = 4.0–6.2 Å). The centres of the trimers and the dihedra (denoted by red and blue circles in Fig. 6c) form a tetrahedron and an octahedron, respectively, with six tetrahedral edges in correspondence to six octahedral vertices (Fig. 6d). Such a relation between the tetrahedron and octahedron graphs is known in graph theory as an edge-to-vertex duality.

Fig. 6. The [(UO2)24(CO3)30O4(OH)12(H2O)8] cluster in: (a) ewingite; (b) its skeletal representation; (c) the U core (the U…U contacts shorter than 4 Å are shown as thick black lines; those between 4 and 6.2 Å as thin black lines; red and blue points indicate centres of the U3 trimers and midpoints of the shared U…U edges of the U4 dihedra, respectively); and (d) the arrangements of the red and blue circles that correspond to the intersection of tetrahedron and octahedron, respectively. After Krivovichev (Reference Krivovichev, Charykova and Krivovichev2020a).
Morrisonite, Ca11[As3+V4+2V5+10As5+6O51]2⋅78H2O, has 13,558 bits of Shannon information per unit cell and, after ewingite, is the second most complex mineral known so far. The vanarsite-group minerals (including morrisonite itself; Kampf et al., Reference Kampf, Hughes, Nash and Marty2016) contain a unique and previously unknown type of the V–As polyoxometalate cluster with the composition [As3+V12As5+6O51]. The cluster consists of twelve (VO6) octahedra forming a wheel- or corona-shaped unit centred by an As3+ cation in trigonal-pyramidal coordination (due to the stereoactivity of a lone-electron pair) and surrounded by six (As5+O4) tetrahedra (Fig. 7). The same polyoxometalate cluster occurs in the crystal structure of vanarsite, NaCa12[As3+2V5+17V4+7As5+12O102]⋅78H2O, but with a different mode of packing of polyoxometalate units. The vanarsite-group minerals form from low-temperature aqueous solutions with V and As derived from the oxidation of primary unoxidised phases.

Fig. 7. The [As3+V4+2V5+10As5+6O51] cluster in morrisonite in (a) polyhedral and (b) skeletal representations. Adapted from Krivovichev (Reference Krivovichev2020a).
Zolotarev et al. (Reference Zolotarev, Krivovichev, Cámara, Bindi, Zhitova, Hawthorne and Sokolova2020) reported the crystal structure of ilmajokite, Na11KBaCe2[Ti12Si37.5O94(OH)31]·29H2O, the third most complex mineral, which was first reported from a hydrothermal vein in Karnasurt Mountain, Lovozero, Kola Peninsula, Russia (Bussen et al., Reference Bussen, Gannibal, Goiko, Mer'kov and Nedorezova1972). The crystal structure is based on a 3D titanosilicate framework consisting of trigonal prismatic titanosilicate (TPTS) clusters centred by Ce3+ in [9]-coordination (Fig. 8). There are two symmetry-independent clusters within the unit cell. In each cluster, three [Ti2O10] dimers of edge-sharing TiO6 octahedra in parallel orientation form a trigonal prism centred by Ce3+ cations. The triple-dimer titanate structure is surrounded by SiO4 tetrahedra to form a TPTS cluster. Four adjacent TPTS clusters are linked into four-membered rings within the (010) plane and linked into ribbons parallel to [$\bar{1}$![]() 01]. The ribbons are organised into layers parallel to (010) and modulated with a modulation wavelength of 32.91 Å and an amplitude of 13.89 Å. The layers are further linked into a titanosilicate framework via additional SiO4 tetrahedra. The Na+, K+, Ba2+ and H2O groups occur in the framework cavities and have different occupancies and coordination environments.
01]. The ribbons are organised into layers parallel to (010) and modulated with a modulation wavelength of 32.91 Å and an amplitude of 13.89 Å. The layers are further linked into a titanosilicate framework via additional SiO4 tetrahedra. The Na+, K+, Ba2+ and H2O groups occur in the framework cavities and have different occupancies and coordination environments.

Fig. 8. Trigonal-prismatic titanosilicate (TPTS) clusters in the crystal structure of ilmajokite shown in (a, c) polyhedral and (b, d) nodal representations. The numbering scheme corresponds to the numbering of Si and Ti atoms from the experiment. The Ce-centred Ti6 trigonal prism is highlighted in yellow. Legend: Si tetrahedra = yellow, Ti octahedra = blue; H2O molecules, Na, K, Ba and Ce atoms are shown as red, light-blue, green, brown, and orange spheres, respectively (after Zolotarev et al., Reference Zolotarev, Krivovichev, Cámara, Bindi, Zhitova, Hawthorne and Sokolova2020).
Complexity-generating mechanisms in minerals
The list of twenty most structurally complex minerals known so far given in Table 3 reveals the following most important complexity-generating mechanisms in minerals:
(1) the presence of large (sometimes nanometre-scale) clusters such as polyoxometalates or related finite-cluster structures (Krivovichev, Reference Krivovichev2020b) isolated from each other; such multinuclear atomic units possess a large number of atoms with different topological functions; the examples are ewingite, morrisonite, vanarsite, bouazzerite and postite; as a rule, natural polyoxometalate minerals are also highly hydrated, with the exception of arsmirandite and lehmannite, which are anhydrous polyoxocuprates formed in volcanic fumaroles (Britvin et al., Reference Britvin, Pekov, Yapaskurt, Koshlyakova, Göttlicher, Krivovichev, Turchkova and Sidorov2020);
(2) the presence of large clusters linked together to form three-dimensional frameworks; the examples are ilmajokite and paddlewheelite (both minerals are also highly hydrated, which contributes greatly to their structural complexities);
(3) the formation of complex three-dimensional modular frameworks formed by cages of different sizes and topologies; this complexity type corresponds to paulingite-group minerals, fantappièite and sacrofanite (members of the sodalite–cancrinite ABC series (Bonaccorsi and Nazzareni, Reference Bonaccorsi and Nazzareni2015; Chukanov et al., Reference Chukanov, Aksenov and Rastsvetaeva2021), tschörtnerite, mendeleevite-(Ce) and rowleyite;
(4) the formation of complex layers with different combinations of modules (chains or rings); this type is characteristic for layered uranyl minerals (such as vandendriesscheite and gauthierite) and layered silicates (parsettensite);
(5) a high hydration state in salts with complex heteropolyhedral units (alfredstelznerite and voltaite-group minerals);
(6) the formation of ordered superstructures of relatively simple structure types; the examples are meerschautite (which is the only sulfide species in the list and was described by Biagioni et al. (Reference Biagioni, Moëlo, Orlandi and Stanley2016) as an expanded derivative of owyheeite) and manitobaite (that has a fivefold superstructure relative to alluaudite (Tait et al., Reference Tait, Ercit, Abdu, Černý and Hawthorn2011)); for further discussion on the relations between superstructures and complexity see Krivovichev et al. (Reference Krivovichev, Panikorovskii, Zolotarev, Bocharov, Kasatkin and Škoda2019a, Reference Krivovichev, Panikorovskii, Yakovenchuk, Selivanova and Ivanyuk2021), Kornyakov et al. (Reference Kornyakov, Vladimirova, Siidra and Krivovichev2021) and Kornyakov and Krivovichev (Reference Kornyakov and Krivovichev2021).
Complexity and symmetry
The Fedorov–Groth statistical law
Fedorov (Reference Fedorov1913, Reference Fedorov1914) and Groth (Reference Groth1921) pointed out that, in general, symmetry of crystalline compounds correlates with their chemical complexity. Less complex compounds (e.g. native elements) tend, on average, to have higher symmetries than compounds consisting of two elements, etc. This empirical observation, known in Russian literature as a Fedorov–Groth law (Shafranovskii, Reference Shafranovskii1973), was recently analysed by Krivovichev and Krivovichev (Reference Krivovichev and Krivovichev2020) using modern crystallographic data for minerals and the concepts of structural and chemical complexity of crystals formulated above. They have shown that there is a strong correlation (Fig. 9; confidence level >0.99) between the atomic chemical (chemIG) and structural (strIG) complexities, and the point-group order |PG| taken as a measure of symmetry (|PG| may be equal to 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48). The relations between these parameters are described by the following exponential functions:



Fig. 9. The plot of average atomic chemical (chemI G) and structural (strI G) complexities of minerals versus the order of the point group, |PG|. After Krivovichev and Krivovichev (Reference Krivovichev and Krivovichev2020).
No good correlations have been obtained for the amounts of chemical and structural information per formula and per reduced unit cell, versus the |PG| values, which is not surprising, as the point-group symmetry of a system is not a function of its size.
The observed strong correlation between the amount of chemical information per atom, chemI G, and the order of the point group, |PG|, indicates that the Fedorov–Groth law is indeed valid and has a statistical meaning. Chemical simplicity measured as an amount of Shannon information per atom on average corresponds to higher symmetry measured as an order of the point group of a mineral.
Complexity and crystal systems
The distribution of minerals among the crystal systems and classes has been extensively discussed in the past, especially in the Russian mineralogical literature (Povarennykh, Reference Povarennykh1966; Shafranovskii and Feklichev, Reference Shafranovskii and Feklichev1982; Shafranovskii, Reference Shafranovskii1983a, Reference Shafranovskii1983b, Reference Shafranovskii1985, Reference Shafranovskii1987, Reference Shafranovskii1988; Dolivo-Dobrovolsky, Reference Dolivo-Dobrovolskii1987, Reference Dolivo-Dobrovolskii1988; Urusov, Reference Urusov2002, Reference Urusov2007; Filatov, Reference Filatov2020). Table 4 provides the modern analysis of the problem that shows that the monoclinic system is most common (>35% of all minerals), followed by orthorhombic (~20%), trigonal (~11.5%) and triclinic (~10.6%) systems (we distinguish between trigonal and hexagonal systems as having threefold and sixfold rotation or inversion axes, respectively). In their analysis of the 1981 data, Shafranovskii and Feklichev (Reference Shafranovskii and Feklichev1982) reported the following sequence of crystal systems: monoclinic (30.8%), orthorhombic (23.4%), cubic (11.2%), hexagonal (9.0%), trigonal (8.7%), tetragonal (8.5%) and triclinic (8.4%). Shafranovskii (Reference Shafranovskii1983a, Reference Shafranovskii1983b, Reference Shafranovskii1987, Reference Shafranovskii1988) suggested that the quantitative distribution of minerals among different crystal systems can be considered as a statistical ‘law of nature’, similar to the Fedorov–Groth law (see above), however Dolivo-Dobrovolsky (Reference Dolivo-Dobrovolskii1988) challenged this view and showed that the number of cubic and triclinic minerals is decreasing and increasing with the historical time, respectively. Urusov (Reference Urusov2002, Reference Urusov2007) supported this view by noticing that most of the rare minerals discovered within last few decades are complex and possess low symmetry. Filatov (Reference Filatov2020) explained the high abundance of monoclinic minerals by the ability of the monoclinic system to adapt complex atomic arrangements, but did not provide any quantitative metrics to support his conclusion. Moreover, Filatov (Reference Filatov2020) based his analysis on old statistical data (e.g. he used 30.5 and 7.4% for the monoclinic and triclinic systems, respectively, which do not correspond to the current situation described in Table 4).
Table 4. Distribution of mineral species among different crystal systems and their average atomic complexities.

The analysis of atomic chemical and structural complexities for different crystal systems shows general agreement with the Fedorov–Groth law with the exception of the trigonal system, which has relatively high values compared to tetragonal and hexagonal systems. The slightly anomalous behavior of the trigonal system is due to the fact that, surprisingly enough, this system is characteristic for many very complex minerals, including, e.g. the members of the cancrinite–sodalite supergroup.
Complexity and space groups
A list of most common space groups observed in minerals according to data for 2020, along with their average atomic structural complexities is shown in Table 5. As the strI G parameter is symmetry-sensitive, it is not surprising that it correlates with the degree of symmetry described by corresponding space groups. Shafranovskii and Feklichev (Reference Shafranovskii and Feklichev1982) analysed the relative abundance of different space groups in minerals based upon the 1981 data and reported the following ten space groups taken in the order of their abundance: P21/c – Pnma – P $\bar{1}$![]() – C2/m – C2/c – R $\bar{3}$
– C2/m – C2/c – R $\bar{3}$![]() m – P21/m – Fd $\bar{3}$
m – P21/m – Fd $\bar{3}$![]() m – Fm $\bar{3}$
m – Fm $\bar{3}$![]() m – P63/mmc. Comparison with the data given in Table 5 indicates the number of monoclinic minerals increased significantly since 1981 relative to the numbers of orthorhombic, trigonal and cubic species. Analysis of Table 3 reveals that, among twenty most structurally complex minerals, four crystallise in the P21/c space group, whereas all others correspond to unique space groups.
m – P63/mmc. Comparison with the data given in Table 5 indicates the number of monoclinic minerals increased significantly since 1981 relative to the numbers of orthorhombic, trigonal and cubic species. Analysis of Table 3 reveals that, among twenty most structurally complex minerals, four crystallise in the P21/c space group, whereas all others correspond to unique space groups.
Table 5. Ten most common space groups for minerals.*

* n min = number of minerals crystallising in the given space group
Urusov and Nadezhina (Reference Urusov and Nadezhina2006) listed 54 space groups that are ‘empty’ of minerals, i.e. have no mineral species crystallised with those symmetries. Our analysis (Table 6) shows that: (1) several ‘empty’ space groups were missed in the compilation and (2) several ‘empty’ space groups have been filled by new mineral species discovered since 2006. For instance, the Pm $\bar{3}$![]() space group, which was ‘empty’ in 2006, was ‘filled’ by the discovery of mendeleevite-(Ce) (Sokolova et al., Reference Sokolova, Hawthorne, Pautov, Agakhanov and Karpenko2011). It is remarkable that the previous compilation of ‘empty’ mineralogical space groups given by Povarennykh (Reference Povarennykh1966) listed 112 groups, i.e. slightly less than half of all possible space groups. In 2021, the number of ‘empty’ space groups (45) is less than 20% of the total number of possible space groups.
space group, which was ‘empty’ in 2006, was ‘filled’ by the discovery of mendeleevite-(Ce) (Sokolova et al., Reference Sokolova, Hawthorne, Pautov, Agakhanov and Karpenko2011). It is remarkable that the previous compilation of ‘empty’ mineralogical space groups given by Povarennykh (Reference Povarennykh1966) listed 112 groups, i.e. slightly less than half of all possible space groups. In 2021, the number of ‘empty’ space groups (45) is less than 20% of the total number of possible space groups.
Table 6. ‘Empty’ space groups (45) in structural mineralogy.*

* The space-group number is given in brackets
** Absent in the list of ‘empty’ groups by Urusov and Nadezhina (Reference Urusov and Nadezhina2006)
*** ‘empty’ group for all inorganic crystal structures
Recently Hummer (Reference Hummer2021) investigated the distribution of mineral species among 32 point groups and demonstrated that the abundance of minerals belonging to each point group approximately obeys a power law with respect to group order, i.e. corresponds to fractal behaviour.
It is interesting that the order of space-group abundance in inorganic compounds (i.e. both minerals and synthetic compounds) differs from that observed in minerals and corresponds to the following sequence (Urusov and Nadezhina, Reference Urusov and Nadezhina2009): Pnma (7.4%), P21/c (7.2%), Fm $\bar{3}$![]() m (5.6%), Fd $\bar{3}$
m (5.6%), Fd $\bar{3}$![]() m (5.1%), P $\bar{1}$
m (5.1%), P $\bar{1}$![]() (4.0%), I4/mmm (4.0%), C2/c (3.8%), P63/mmc (3.4%), C2/m (3.4%) and Pm $\bar{3}$
(4.0%), I4/mmm (4.0%), C2/c (3.8%), P63/mmc (3.4%), C2/m (3.4%) and Pm $\bar{3}$![]() m (3.0%). These data show that the total kingdom of inorganic crystal structures is, on average, higher in symmetry relative to the mineral kingdom, which is rather remarkable. One may speculate that this tendency is due to the limited chemical diversity of natural systems compared to synthetic ones, which provides a broad avenue for synthetic chemical exploration of chemically simple, but naturally unstable or geochemically unusual combination of elements. In fact, synthetic chemists rarely study systems of more than three or four elements. Even though they consider combinations of elements not found in Nature, they very rarely attempt to study compounds in a system with seven or eight elements, as are often found in Nature. Therefore, the trend of fewer elements leading to higher average symmetry is reflected in synthetic inorganic chemistry. High temperatures of synthesis (compared to all of the low-temperature weathering/alteration minerals) may also play a role. We may hypothesise that the average chemical simplicity of synthetic systems results in their higher symmetry, according to the Fedorov–Groth law, which is statistically valid for large numbers of observations (see above).
m (3.0%). These data show that the total kingdom of inorganic crystal structures is, on average, higher in symmetry relative to the mineral kingdom, which is rather remarkable. One may speculate that this tendency is due to the limited chemical diversity of natural systems compared to synthetic ones, which provides a broad avenue for synthetic chemical exploration of chemically simple, but naturally unstable or geochemically unusual combination of elements. In fact, synthetic chemists rarely study systems of more than three or four elements. Even though they consider combinations of elements not found in Nature, they very rarely attempt to study compounds in a system with seven or eight elements, as are often found in Nature. Therefore, the trend of fewer elements leading to higher average symmetry is reflected in synthetic inorganic chemistry. High temperatures of synthesis (compared to all of the low-temperature weathering/alteration minerals) may also play a role. We may hypothesise that the average chemical simplicity of synthetic systems results in their higher symmetry, according to the Fedorov–Groth law, which is statistically valid for large numbers of observations (see above).
For organic compounds, the P21/c group is the most common (46%), followed by P $\bar{1}$![]() (20%), C2/c (7%), Pbca (6%), P212121 (5%), P21 (3%), Pna21 (2%) and Pca21 (2%) (Rekis, 2020). The space-group distribution pattern here is drastically different from that observed in minerals and inorganic compounds, though the leading role of the P21/c group is again remarkable.
(20%), C2/c (7%), Pbca (6%), P212121 (5%), P21 (3%), Pna21 (2%) and Pca21 (2%) (Rekis, 2020). The space-group distribution pattern here is drastically different from that observed in minerals and inorganic compounds, though the leading role of the P21/c group is again remarkable.
As far as we know, there is no comprehensive explanation for the space-group distribution in crystals. Hellner and Sowa (Reference Hellner and Sowa1985) and Dolivo-Dobrovolsky (Reference Dolivo-Dobrovolskii1988) pointed out that space groups with large percentages of characteristic orbits (i.e. orbits that possess symmetry of the generating space groups and not higher) have higher abundance. However, as was mentioned by Urusov and Nadezhina (Reference Urusov and Nadezhina2009), this cannot explain the predominance of the P21/c space group that contains only one kind of characteristic orbit, whereas all its orbits of other kinds are non-characteristic.
Complexity, symmetry and temporal dynamics of mineralogical research
It was mentioned above that our information on the distributions of minerals among different crystal systems has changed significantly within the last four decades with the relative increase of the number of triclinic minerals. This tendency is related directly to the general tendency of temporal complexification of mineralogical objects in the history of mineralogical research. Kaußler and Kieslich (Reference Kaußler and Kieslich2021) provided a temporal analysis of complexity parameters of crystal structures in the history of crystallography, demonstrating that the atomic structural complexities have increased continuously since the birth of X-ray diffraction analysis of crystals in 1914. With time, more and more complex crystal structures are solved and refined, thanks to the enormous advances in diffraction techniques, including recent advancements in detector technologies, X-ray sources and electron diffraction, as well as improved computational methods for the direct solution of complex crystal structures.
We have done a similar analysis of complexity of minerals in the history of mineralogy, starting from 1875, when Weisbach's Synopsis mineralogica was published that contained the full list of minerals (631 species) known at the time (Weisbach, Reference Weisbach1875). The lists of minerals were then split into quarters of a century, where for each mineral the year of its discovery was assigned as the year of publication of its description according to bibliographic data provided in the International Mineralogical Association (IMA) Database of Mineral Properties (https://rruff.info/ima/). It is important to note that mineralogical knowledge was revised according to the IMA rules in existence at that time. For instance, in plagioclases, only two species were recognised, i.e. anorthite and albite, whereas their varieties such as bytownite, labradorite, andesine, and oligoclase were not considered as separate mineral species, despite their recognition as such in the 19th and 20th centuries. The temporal lists of minerals have been used to calculate their average complexities (arithmetic means). The numerical data are given in Table 7, whereas their visualisation is presented in Fig. 10. Fig. 10a shows the temporal dynamics of mineralogical discoveries since 1875 with steps of 25 years, whereas Figs 10b and c show the increasing chemical and structural complexity of human knowledge of the mineral kingdom in the history of mineralogy. With time, more and more chemically and structurally complex minerals have been discovered, which is exemplified by the family of natural polyoxometalates that belong to the most complex mineral species known so far (see above).

Fig. 10. Temporal dynamics of complexity in mineralogical research: average chemical and structural complexity parameters for the total lists of mineral species in different times.
Table 7. Average chemical and structural complexity parameters for minerals in temporal dynamics.

The temporal dynamics of distribution of known minerals among crystal systems is given in Table 8 and visualised in Fig. 11. It can be seen clearly that, in the history of mineralogy, the percentage of triclinic minerals has continuously increased, whereas that of cubic minerals has continuously decreased. It is interesting that the percentage of hexagonal minerals has also increased, though this trend is less pronounced compared to that of triclinic minerals. The most remarkable change is observed for cubic minerals; their percentage has decreased by ~5% since 1875. Our results reported here are in agreement with similar observations made by Dolivo-Dobrovolsky (Reference Dolivo-Dobrovolskii1988), who also demonstrated the rise of triclinic and the decline of cubic mineral species in the history of mineralogical research.

Fig. 11. Relative percentages of crystal systems for minerals known in different time periods of mineralogical research. Legend: Tricl = triclinic; Mon = monoclinic; Orth = orthorhombic; Tetr = tetragonal; Trig = trigonal; Hex = hexagonal; and Cub = cubic.
Table 8. Temporal dynamics of the distribution of minerals among different crystal systems from 1875 to 2020 (in %).

Complexity, paragenetic modes and mineral evolution
The idea that the mineral kingdom has changed in diversity and distribution with geological time dates back to the 1980s (Zhabin, Reference Zhabin1981; Yushkin, Reference Yushkin1982), but the most important revolutionary contribution to the field is due to the recent works by Hazen and Morrison, and coworkers (Hazen and Morrison, Reference Hazen and Morrison2020, Reference Hazen and Morrison2021a; Morrison and Hazen, Reference Morrison and Hazen2020, Reference Morrison and Hazen2021; Hazen et al., Reference Hazen, Morrison and Prabhu2021, etc.). Krivovichev et al. (Reference Krivovichev, Krivovichev and Hazen2018a) used the chronological lists provided by Hazen et al. (Reference Hazen, Papineau, Bleeker, Downs, Ferry, McCoy, Sverjensky and Yang2008) and Hazen (Reference Hazen2013), who subdivided mineral evolution into four partially overlapping eras and ten stages, each of which saw the expansion of mineralogical diversity and/or variation in relative mineral abundances. The starting point of mineral evolution is that of the ‘ur-minerals’, the twelve earliest mineral phases to appear in the pre-solar nebulae (I). Chondritic meteorites incorporate ~60 primary mineral phases, which constitute the second phase (II). For the Hadean Eon, Hazen (Reference Hazen2013) estimated 425 mineral species (III), whereas post-Hadean processes were responsible for the appearance of more than 5000 mineral species known today (IV). Figure 12 shows that both chemical and structural complexity are gradually increasing in the course of mineral evolution. However, one should take into account that many very complex minerals (especially surficial ones) have limited stability and are unlikely to survive for very long geological periods of time (Mills and Christy, Reference Mills and Christy2019).

Fig. 12. Mean chemical and structural complexities for minerals occurring in different eras of mineral evolution (1 = 'ur-minerals'; 2 = minerals of chondritic meteorites; 3 = minerals of the Hadean epoch; 4 = minerals of the post-Hadean era): (a) Shannon information per atom and (b) per unit cell or formula unit. After Krivovichev et al. (Reference Krivovichev, Krivovichev and Hazen2018a).
In a recent paper, Hazen and Morrison (Reference Hazen and Morrison2021b) subdivided all known minerals into 57 paragenetic modes, most of which can be assigned to a particular stage of mineral evolution. The average chemical and structural complexities for different paragenetic modes and respective stages of mineral evolution are given in Supplementary table S1. The evolutionary dynamics of mineral diversity and total structural and chemical complexities with the passage of geological time are shown in Figure 13. Both diversity and complexity increase dramatically in association with the formation of Earth's continental crust, the initiation of plate tectonics, and the Great Oxidation event. For paragenetic modes, the highest complexity is associated with secondary uranium mineralisation (P27 and P47f) and basalt-hosted zeolite crystallisation (P10). Both modes are associated with low-temperature hydrous activity, paralleling the conclusion by Hazen and Morrison (Reference Hazen and Morrison2021b) that “by far the most significant factor in enhancing Earth's mineral diversity has been its dynamic hydrological cycle”.
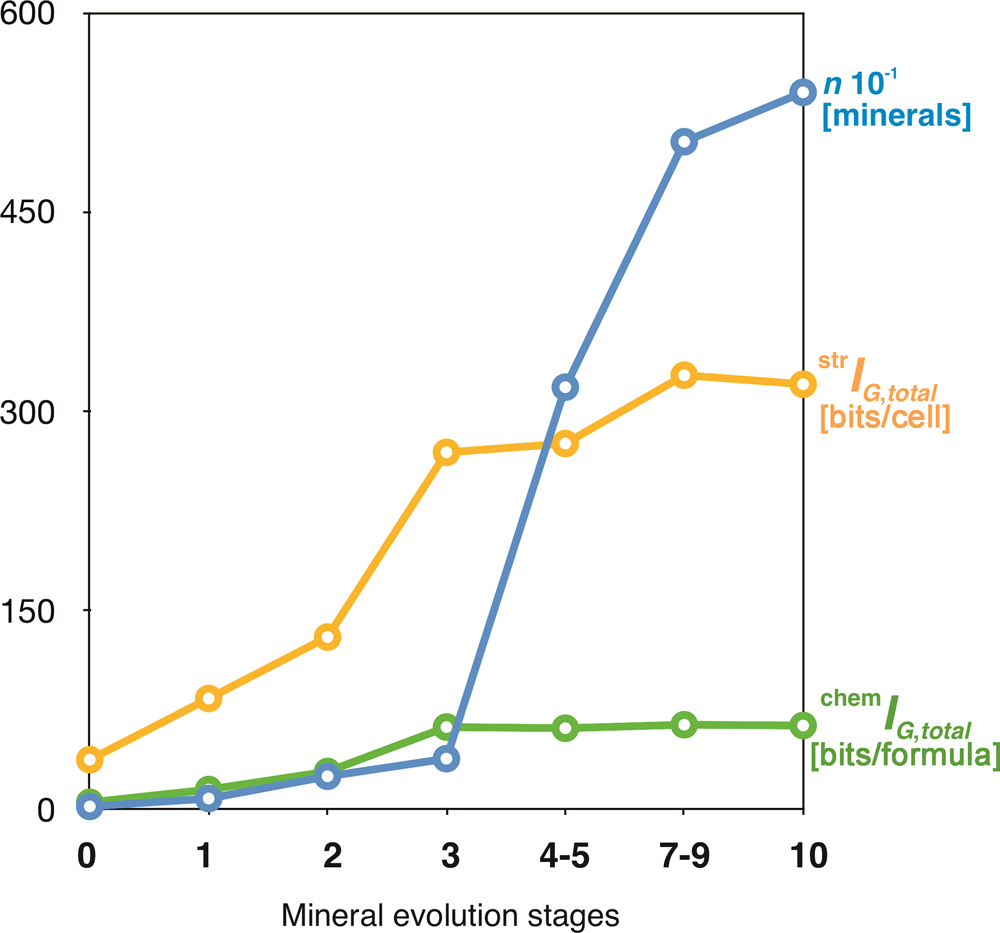
Fig. 13. The evolution of mineral diversity (blue), total structural (yellow) and total chemical (green) complexities at different stages of mineral evolution.
Further directions
Structural complexity in Data-Driven Discovery
Hazen (Reference Hazen2014) and Hazen et al. (Reference Hazen, Downs, Eleish, Fox, Gagné, Golden, Grew, Hummer, Hystad, Krivovichev, Li, Liu, Ma, Morrison, Pan, Pires, Prabhu, Ralph, Runyon and Zhong2019) advocated Data-Driven Discovery as a new direction in the science of mineralogy that deals with the analysis of large volumes of data on chemical composition, crystal structure, physical properties and geological origins of minerals that have been accumulated in scientific literature over several last hundred years. The implementation of various numerical techniques (e.g. network analysis (Morrison et al., Reference Morrison, Liu, Eleish, Prabhu, Li, Ralph, Downs, Golden, Fox, Hummer, Meyer and Hazen2017, Reference Morrison, Buongiorno, Downs, Eleish, Fox, Giovannelli, Golden, Hummer, Hystad, Kellogg, Kreylos, Krivovichev, Liu, Merdith, Prabhu, Ralph, Runyon, Zahirovic and Hazen2020)) would provide us with new insights into distribution and diversity of minerals through space and time. Structural and chemical complexity are important characteristics of minerals reflecting their formation and evolution in geological environments. Incorporation of complexity data into modern mineralogical databases (such as GEMI (Prabhu et al., Reference Prabhu, Morrison, Eleish, Zhong, Huang, Golden, Perry, Hummer, Ralph, Runyon, Fontaine, Krivovichev, Downs, Hazen and Fox2021)) provides additional possibilities to extract novel and interesting regularities, due to the general relations between complexity and configurational entropy of crystalline solids (Krivovichev, Reference Krivovichev2016).
Structural complexity and thermodynamics
The relations between structural complexity and temperature and pressure have been discussed briefly by Krivovichev (Reference Krivovichev2012, Reference Krivovichev2013) and is beyond the topic of the current review. However, several general points can be outlined here. As the structural complexity strIG ,mix, defined by equations (27) and (29) as consisting of the complexity of atomic architecture and positional disorder, is related to configurational entropy, and the latter is related to vibrational entropy, it can be expected that structural complexity decreases with increasing temperature and increases with increasing pressure. The first trend is confirmed by numerous data, including recent results on phase transitions in minerals (e.g. Avdonceva et al., Reference Avdontceva, Krzhizhanovskaya, Krivovichev and Yakovenchuk2015a, Reference Avdontceva, Zolotarev and Krivovichev2015b). Increasing temperature also generally leads to an increase in structural disorder. Filatov (Reference Filatov2011) emphasised the principle that increasing symmetry is often correlated with an increase of temperature. However, the principle of decreasing complexity with increasing temperature includes symmetry as one of its aspects and better describes the behaviour of solids under heating. For instance, Ismagilova et al. (Reference Ismagilova, Zhitova, Krivovichev, Sergeeva, Nuzhdaev, Anikin, Krzhizhanovskaya, Nazarova, Kupchinenko and Zolotarev2021) noticed that there are two natural Cu3(VO4)2 polymorphs, pseudolyonsite and mcbirneyite, that correspond to high- and low-temperature modifications, respectively, which conforms well with their densities, 4.71 and 4.48 g.cm–3, respectively. However, pseudolyonsite has higher (monoclinic) symmetry than mcbirneyite (triclinic polymorph), which is in obvious contradiction with the rule emphasised by Filatov (Reference Filatov2011). In contrast, structural complexity calculations show that triclinic mcbirneyite is structurally simpler (36 bits/cell) than monoclinic pseudolyonsite (72 bits/cell), in agreement with the observation that, generally, complexity decreases upon heating. However, this empirically derived tendency may be violated as, for example, was shown for BiSeO3Cl (Aliev et al., Reference Aliev, Kovrugin, Colmont, Terryn, Huvé, Siidra, Krivovichev and Mentré2014). The low- and high-temperature modifications, α- and γ- BiSeO3Cl, respectively, have the same complexity, 62 bits/cell. However, the intermediate β-phase is very complex with strIG,total = 4706 bits/cell. Aliev et al. (Reference Aliev, Kovrugin, Colmont, Terryn, Huvé, Siidra, Krivovichev and Mentré2014) showed that the extreme complexity of this phase is due to its transitional character, as its structure can be considered a ‘frozen’ transitional state between the low- and high-temperature forms. In general, transitional crystalline states existing on the border between stability fields of simple phases, may possess extraordinarily high complexity (Gurzhiy et al., Reference Gurzhiy, Tyumentseva, Krivovichev, Krivovichev and Tananaev2016).
Hazen and Navrotsky (Reference Hazen and Navrotsky1996) analysed the influence of pressure upon order–disorder reactions and showed that, in the majority of cases, increasing pressure is associated with decreasing positional disorder, though there are exceptions to this rule (Deng et al., Reference Deng, Kang, Croft, Li, Shen, Zhao, Yu, Jin, Kotliar, Liu, Tyson, Tappero and Greenblatt2020). The ordering reactions mean that structural complexity is increasing. Krivovichev (Reference Krivovichev2021a) recently reviewed the crystal chemistry of high-pressure silicates and showed that, in many cases, structural complexity increases with pressure, but only when coordination numbers of atoms remain constant during phase transitions from low- to high-pressure modification. However, even then the situation is not straightforward, as can be seen from the high-pressure phase transitions of coesite, SiO2. Bykova et al. (Reference Bykova, Bykov, Černok, Tidholm, Simak, Hellman, Belov, Abrikosov, Liermann, Hanfland, Prakapenka, Prescher, Dubrovinskaia and Dubrovinsky2018) reported five coesite polymorphs, numbered from I to V with increasing pressure. The coesite-I → coesite-II → coesite-III phase transitions are displacive and do not modify the topology of the framework; Si atoms remain in tetrahedral coordination. Along the pathway, the symmetry is decreasing (C2/c → P21/n → P $\bar{1}$![]() ), which corresponds to the increasing number of symmetrically independent sites and the increasing structural information per atom (2.752 → 4.585 → 5.198 bits/atom). However, the total structural information does not behave similarly (66 → 440 → 374 bits/cell). The coesite-IV and V polymorphs contain tetra-, penta- and hexa-coordinated Si and have the same complexity, 4.585 bits/atom and 220 bits/cell. The change in coordination number may modify the complexity behaviour unpredictably. The most probable reason is that the increase in pressure results in the increase of vibrational entropy, which is not a direct function of configurational entropy and structural complexity described by equations (27) and (28).
), which corresponds to the increasing number of symmetrically independent sites and the increasing structural information per atom (2.752 → 4.585 → 5.198 bits/atom). However, the total structural information does not behave similarly (66 → 440 → 374 bits/cell). The coesite-IV and V polymorphs contain tetra-, penta- and hexa-coordinated Si and have the same complexity, 4.585 bits/atom and 220 bits/cell. The change in coordination number may modify the complexity behaviour unpredictably. The most probable reason is that the increase in pressure results in the increase of vibrational entropy, which is not a direct function of configurational entropy and structural complexity described by equations (27) and (28).
Structural complexity and crystallization
Krivovichev (Reference Krivovichev2013) provided an overview of relations between structural complexity and metastable crystallisation based upon the Goldsmith's simplexity principle that states that simple structures crystallise more easily. This idea was supported by many subsequent observations, including metastable feldspar polymorphs (Zolotarev et al., Reference Zolotarev, Krivovichev, Panikorovskii, Gurzhiy, Bocharov and Rassomakhin2019; Krivovichev, Reference Krivovichev and Krivovichev2020, and references therein), perovskite-group minerals (Zaitsev et al., Reference Zaitsev, Zhitova, Spratt, Zolotarev and Krivovichev2017), uranyl minerals (Plášil et al., Reference Plášil2018b, Reference Plášil2018c), sulfates (Plášil et al., Reference Plášil, Petříček and Majzlan2017; Majzlan et al., Reference Majzlan, Dachs, Benisek, Plášil and Sejkora2018), phosphates and arsenates (Krivovichev et al., Reference Krivovichev, Zolotarev and Popova2016; Krivovichev, Reference Krivovichev2017; Kolitsch et al., Reference Kolitsch, Weil, Kovrugin and Krivovichev2020), Cu2(OH)3Cl polymorphs (Krivovichev et al., Reference Krivovichev, Hawthorne and Williams2017), borates (Grew et al., Reference Grew, Krivovichev, Hazen and Hystad2016), borosilicates (Cempírek et al., Reference Cempírek, Grew, Kampf, Ma, Novák, Gadas, Škoda, Vašinová-Galiová, Pezzotta, Groat and Krivovichev2016), oxalates (Huskić et al., Reference Huskić, Novendra, Lim, Topić, Titi, Pekov, Krivovichev, Navrotsky, Kitagawa and Friščić2019), etc. In his review on metastable-mineral formation in oxidation zones and mine wastes, Majzlan (Reference Majzlan2020) recently noted that “a quantitative link…” between structural complexity and metastability “…is missing”. Indeed, no equation could be written that would directly relate structural information and the ease of crystallisation, as complexity is not the only factor that defines the sequence of crystallisation. An example of non-linear behaviour is given by TiO2 polymorphs. It is usually assumed that, under ambient conditions, anatase and brookite are metastable, whereas rutile is thermodynamically stable (Ranade et al., Reference Ranade, Navrotsky, Zhang, Banfield, Elder, Zaban, Borse, Kulkarni, Doran and Whitfield2002). The structural complexity parameters of the three phases do not conform to Goldsmith's principle, as anatase and rutile have the same complexity (0.918 bits/atom and 5.5 bits/cell), whereas brookite is the most complex among these TiO2 polymorphs (1.585 bits/atom and 38 bits/cell). This example shows that the correlation between structural complexity and metastability is not straightforward and outlines an empirical tendency rather than rigorous regularity. The detailed account of the relations between complexity and metastability will be published elsewhere.
Structural complexity and modularity
Modularity is an important structural principle for minerals and inorganic compounds, as many mineral structures can be considered as built up from modules (blocks) derived from simple archetype structures and recombined in a particular way (Ferraris et al., Reference Ferraris, Makovicky and Merlino2004). As one could imagine an infinite number of modular combinations, it could be expected that the number of possible derivative structures is infinite. However, only a few combinations are observed in Nature, and those are usually the simplest possible. Pankova et al. (Reference Pankova, Krivovichev, Pekov, Grew and Yapaskurt2018b) showed that, in the kurchatovite family, only the two simplest variations are realised in Nature that can be generated according to the given structural principles of modular combinations. The principle of simplicity in modular series and its relation to abundances of structural architectures will be discussed in detail elsewhere.
Summary and outlook
Structural and chemical complexity is an important parameter relevant to the constitution, origin and behaviour of minerals. Quantitative measures of complexity that are applicable to any mineral are therefore useful numerical characteristics that can be used to reveal hidden relations among structure, composition and configuration entropy of crystalline solids, on one hand, and their stability and formation conditions on the other. The key concept behind the complexity parameters is that of information. Minerals do not have a material carrier of information, which is present in living organisms and viruses in the form of a genome, i.e. the sequence of nucleotides that govern the synthesis of proteins. Instead, information is encoded in minerals in various forms, from which an idealised crystal structure and idealised end-member formula are just the first and basic approximations. Further developments may include understanding and quantification of real crystal chemistry that includes chemical admixtures, short-range order, defects and information encoded in microstructural irregularities. The present review further emphasises the importance of the fundamental concept of information in mineralogy, which provides a different perspective to look at such traditional concepts as symmetry. From the viewpoint of an information approach, symmetry is seen as a way to minimise the information content, i.e. as the principle of information minimisation. The advances in experimental techniques provide new and deeper understanding of mineralogical objects, which is evident, in particular, in the modern developments in structural and descriptive mineralogy. For instance, the new discoveries of polyoxometalate minerals in the 21st century witness that the role of polynuclear atomic clusters in geochemical processes may be underestimated and that new models are needed (Rustad, Reference Rustad2010; Friis and Casey, Reference Friis and Casey2018). To conclude, the developments in complexity theory of minerals provide a new way to look at mineralogical objects, which complement the existing theoretical and experimental approaches.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1180/mgm.2022.23
Acknowledgements
We are grateful to Associate Editor Andrew G Christy, Frank Hawthorne and an anonymous reviewer for useful reviews of the first version of the manuscript. This work was supported by the Russian Science Foundation (grant 19-17-00038 to S.V.K.). RMH and SMM acknowledge support from the NASA Astrobiology Institute (Cycle 8) ENIGMA: Evolution of Nanomachines In Geospheres and Microbial Ancestors (80NSSC18M0093); findings expressed herein are those of the authors and do not necessarily reflect the views of the National Aeronautics and Space Administration.



























