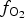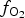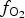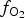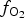Introduction
Oxide minerals of the spinel group (from here on referred to as spinels), alongside being important constituents of the uppermost mantle, are common accessory minerals in both igneous and metamorphic rocks, and commonly occur as detrital grains in sedimentary deposits. Furthermore, spinels are found in a wide range of extra-terrestrial samples with their ubiquity suggesting an early role in the formation of the solar system (Roeder, Reference Roeder1994). Spinel-group minerals are useful petrogenetic indicators in terrestrial magmas because they form complex solid solutions which crystallize in a wide range of magmatic compositions. Spinels can be found as both early- and late-crystallizing phases during magma fractionation, and are often the first phase to form (Barnes and Roeder, Reference Barnes and Roeder2001). When compared to other high-temperature igneous minerals such as olivine, spinels are fairly resistant to chemical and physical alteration (Cookenboo et al., Reference Cookenboo, Bustin and Wilks1997). Therefore, detrital spinel found in early sedimentary deposits could record conditions (e.g. temperature, redox conditions and pressure) prevalent in early Earth's history.
Spinels tend to have high partition coefficients for trace elements in magmatic systems. Consequently, crystallization of a spinel phase strongly influences the budgets of trace elements. The partitioning of elements between spinels and silicate melts is affected strongly by temperature (T), oxygen fugacity (![]() $f_{{\rm O}_{\rm 2}}$) and spinel composition (Righter et al., Reference Righter, Leeman and Hervig2006), and may also be affected by pressure (P). Spinel geochemistry can, therefore, be used as an important tool in determining fractionation trends of magmas and the trace-element budget of primary basaltic magmas (Wijbrans et al., Reference Wijbrans, Klemme, Berndt and Vollmer2015), which gives insight into the source region of these melts in the mantle. The potential of spinels to determine
$f_{{\rm O}_{\rm 2}}$) and spinel composition (Righter et al., Reference Righter, Leeman and Hervig2006), and may also be affected by pressure (P). Spinel geochemistry can, therefore, be used as an important tool in determining fractionation trends of magmas and the trace-element budget of primary basaltic magmas (Wijbrans et al., Reference Wijbrans, Klemme, Berndt and Vollmer2015), which gives insight into the source region of these melts in the mantle. The potential of spinels to determine ![]() $f_{{\rm O}_{\rm 2}}$ is important for further understanding magmatic differentiation, mineral assemblages and elemental partitioning (Sato, Reference Sato1978). As well as controlling the chemistry of magmas, spinel composition is sensitive to changes in the chemistry of the surrounding magma because of several substituting cations which can subtly change according to the physico-chemical conditions of the parental melt (Arai, Reference Arai1992).
$f_{{\rm O}_{\rm 2}}$ is important for further understanding magmatic differentiation, mineral assemblages and elemental partitioning (Sato, Reference Sato1978). As well as controlling the chemistry of magmas, spinel composition is sensitive to changes in the chemistry of the surrounding magma because of several substituting cations which can subtly change according to the physico-chemical conditions of the parental melt (Arai, Reference Arai1992).
The complex chemistry of spinels in igneous systems is due to the extensive solid solutions and the extent of cation disorder across different crystallographic sites. Diversity in natural spinels also arises from the valence of the cations found in either the tetrahedral or octahedral sites. Divalent, trivalent and tetravalent cations can all be accommodated into the spinel structure, and many transitional elements can be present in varying amounts of multiple valences. The general formula of spinels is typically expressed as AB2O4, where A and B are different cations. Common cations include Mg, Fe, Al, Zn, Mn, Cr, Ga, Ti and Si. Spinels are also an important mineral group for industrial and technological applications due to their extraordinary catalytic, electrical, optical and magnetic properties (Carta et al., Reference Carta, Marras, Loche, Mountjoy, Ahmed and Corrias2013), which arises from their ability to incorporate many transitional elements into their structure (e.g. Fe, Mo, Zn, Ti, Cr, Mn and V).
Galaxite (MnAl2O4) and jacobsite (MnFe2O4) are two Mn spinel end-members. In nature, galaxite often forms in carbonate-rich silica under-saturated metamorphosed Mn deposits (Anthony et al., Reference Anthony, Bideaux, Bladh and Nichols1997). Jacobsite generally forms as a primary mineral or alteration product in similar metamorphosed Mn deposits (Anthony et al., Reference Anthony, Bideaux, Bladh and Nichols1997). The structure of jacobsite, galaxite, and other oxide minerals with a spinel structure, consists of oxygen atoms arranged in a cubic close packed (ccp) structure, with cations filling ⅛ of the tetrahedral (T) and ½ of the octahedral (M) sites. An excess of metal cations will occupy normally vacant interstitial sites (Fleet Reference Fleet1981; Henderson et al., Reference Henderson, Pearce, Charnock, Harrison and Rosso2016). The typical space group symmetry of spinels is Fd ![]() $\bar 3$m. In an ideal ‘2–3 spinel’ structure, divalent cations are housed on the T site, whilst trivalent cations are present on the M site. Spinel-group minerals typically display variable degrees of disorder of A and B cations across the T and M sites (Redfern et al., Reference Redfern, Harrison, O'Neill and Wood1999). The amount of cation disorder can be described using the inversion parameter i, which is defined by the equation:
$\bar 3$m. In an ideal ‘2–3 spinel’ structure, divalent cations are housed on the T site, whilst trivalent cations are present on the M site. Spinel-group minerals typically display variable degrees of disorder of A and B cations across the T and M sites (Redfern et al., Reference Redfern, Harrison, O'Neill and Wood1999). The amount of cation disorder can be described using the inversion parameter i, which is defined by the equation:
When i = 0, a ‘2–3’ spinel is described as completely normal (TAMB2O4), whereas i = 1 describes an ‘inverse’ configuration (TBM(AB)2O4), and an inversion parameter of 0.67 indicates a completely disordered spinel. In a completely normal spinel, A ions fully occupy the T sites, whilst the M site is filled by B cations. Inverse spinels have half of the B and all the A cations on the M site, whilst the other B cations fully occupy the T sites. At high temperatures, i tends toward complete disorder for all compositions. ‘4–2’ spinels are rarer than ‘2–3’ spinels and have a tetravalent A cation and divalent B cation (Biagioni and Pasero, Reference Biagioni and Pasero2014).
Jacobsite is a nominally ‘normal’ Fe3+–Mn2+ ‘2–3’ spinel. However, the actual assignment of cation oxidation states is difficult due to: (1) the multivalence characteristic of both Mn and Fe; (2) the equilibrium Mn2+ + Fe3+ ⇌ Mn3+ + Fe2+; (3) electron hopping between cation sites (Biagioni and Pasero, Reference Biagioni and Pasero2014); and (4) the similar atomic number of these elements. Fe–Mn spinels are of particular interest to industry because they provide improved performance catalysts in Fischer–Tropsh synthesis (Herranz et al., Reference Herranz, Rojas, Ojeda, Pérez-Alonso, Terreros, Pirota and Fierro2006), are used as negative temperature coefficient (NTC) thermistors (Battault et al., Reference Battault, Legros and Rousset1995), act as contrasting agents in MRI imaging (Lu et al., Reference Lu, Ma, Sun, Xia, Liu, Wang, Zhao, Gao, Gong and Song2009), and as hyperthermia agents in cancer treatment (Kim et al., Reference Kim, Zeng, Ng and Brazel2009). Galaxite is also a ‘normal’ spinel, although in this case assignment of the Mn oxidation state is simpler due to the significant difference in atomic number between Al and Mn, as well as the single valence state of Al within spinels.
Recent work on spinel-group minerals within Earth sciences has focussed on the development of calibrated thermometers, barometers, and oxygen barometers based on the partitioning of redox sensitive trace elements between spinel and melts, for use when conventional methods cannot be performed (e.g. Canil Reference Canil1999; Righter et al., Reference Righter, Leeman and Hervig2006; Burger et al., Reference Burger, Shearer, Papike, Bell and Muttik2016; Arató and Audétat, Reference Arató and Audétat2017). Manganese is a redox sensitive element which readily substitutes into both the tetrahedral and octahedral crystallographic sites in the spinel structure, and can be present either as Mn2+, Mn3+ and/or Mn4+. Mn can also be present in multiple oxidation states on the same or different sites. However, little is known on the behaviour of Mn in the spinel structure as a function of P, T and ![]() $f_{{\rm O}_{\rm 2}}$, or the extent to which Mn speciation and partitioning into spinels can be used to probe
$f_{{\rm O}_{\rm 2}}$, or the extent to which Mn speciation and partitioning into spinels can be used to probe ![]() $f_{{\rm O}_{\rm 2}}$ conditions in magmas.
$f_{{\rm O}_{\rm 2}}$ conditions in magmas.
Measuring valance states can be challenging in the simple end-member spinels, and is further complicated in the solid solutions. The arrangement of cations in the spinel structure is often investigated using X-ray diffraction (XRD) and neutron diffraction (ND) data. However, this data can be ambiguous in spinels that contain cations with similar scattering properties, and is further complicated by the coupled effects of changes in valence state and ordering. Determining the oxidation state of cations on the T and M sites is also very difficult as most techniques cannot differentiate the valence state of cations. 57Fe Mössbauer spectra provides important data for the valence, coordination, and ordering of Fe cations but fails to distinguish Fe3+ and Fe2+ above the Verwey transition temperature (Henderson et al., Reference Henderson, Pearce, Charnock, Harrison and Rosso2016). Furthermore, Mössbauer cannot always distinguish Fe3+ site occupation between M and T sites (Zhang et al., Reference Zhang, Wang, Chakoumakos and Yin1998), and is only applicable for cations with a Mössbauer spectrum. X-ray absorption near edge structure (XANES) spectroscopy is a method which is becoming increasingly common in determining oxidation state and coordination state in geological materials. Unlike electron energy loss spectroscopy (EELS), XANES is a non-destructive technique which can obtain spectra from samples mounted for optical and electron microscopy. As spinel is an isotropic mineral, XANES spectra can be recorded from any grain without having to account for the effects of crystallographic orientation (Berry et al., Reference Berry, Yaxley, Woodland and Foran2010).
Here, XANES K-edge data are used to provide averaged site information, which is combined with single-crystal X-ray diffraction (SC-XRD) structural refinements and compositional data from electron microprobe analyses (EMPA) to provide an estimate for cation coordination and valence in synthetic jacobsite- and galaxite-like spinels (from here on, just referred to as jacobsite and galaxite). This multidisciplinary approach is used to estimate the cation distribution and oxidation state for Al, Mn and Fe across the T and M sites, using previously published cation site preferences. Varying ![]() $f_{{\rm O}_{\rm 2}}$ conditions during synthesis are used to determine the effect of redox on either the amount, valence, or distribution of Al, Mn and Fe in jacobsite and galaxite to determine the potential of an oxy-geobarometer based on Mn-in-spinel.
$f_{{\rm O}_{\rm 2}}$ conditions during synthesis are used to determine the effect of redox on either the amount, valence, or distribution of Al, Mn and Fe in jacobsite and galaxite to determine the potential of an oxy-geobarometer based on Mn-in-spinel.
Mineral synthesis
Single crystals of jacobsite and galaxite were synthesized using a similar flux growth method to that of Andreozzi (Reference Andreozzi1999). Starting mixtures were prepared from stoichiometric proportions of analytical grade powders (MnO2, Al2O3 and Fe2O3) and mixed with anhydrous borax (Na2B4O7), the flux compound. The starting material was weighed and homogenized by grinding under acetone in an agate mortar before being placed in a Pt/Au (5%) crucible. This type of crucible was selected due to its low wettability and high resistance to chemical attack at high temperatures under reducing conditions. Experimental runs were performed using a platinum wound vertical tube gas-mixing furnace with Bronkhorst mass flow controllers. Oxide and flux mixes were heated to 1200°C for 1 hr before cooling at 12.5°C/hr to the final run temperature of 900°C, then held for 24 hr, before being quenched rapidly. Each experiment (except for Ga60, which was quenched by quickly raising the charge out of the hotspot) was drop quenched into water upon completion of the run. A mixture of CO2/H2 gas was used to control the oxygen fugacity conditions during synthesis (Deines et al., Reference Deines, Nafziger, Ulmer and Woermann1974), with ![]() $f_{{\rm O}_{\rm 2}}$ values confirmed using an Australian Oxytrol Systems solid zirconia electrolyte oxygen sensor (SIRO2 sensor). Runs JcAC and GaAC were both run with the furnace open to air (Log
$f_{{\rm O}_{\rm 2}}$ values confirmed using an Australian Oxytrol Systems solid zirconia electrolyte oxygen sensor (SIRO2 sensor). Runs JcAC and GaAC were both run with the furnace open to air (Log ![]() $f_{{\rm O}_{\rm 2}}$ (air) = –0.68 for all temperatures, if we assume it is behaving as an ideal gas). Runs suffixed by 93, 90 and 60 indicate the %CO2 used in the gas mix, and equate to log
$f_{{\rm O}_{\rm 2}}$ (air) = –0.68 for all temperatures, if we assume it is behaving as an ideal gas). Runs suffixed by 93, 90 and 60 indicate the %CO2 used in the gas mix, and equate to log ![]() $\hskip 2pt f_{{\rm O}_{\rm 2}}$= –13.8, –14.2 and –15.8, respectively, at 900°C. Recovered spinels were mounted in epoxy, ground, and polished using standard diamond solutions for XANES analysis and EMPA. Individual crystals of each sample were selected for high-quality XRD analysis, and examined optically to ensure absence of twinning and inclusions.
$\hskip 2pt f_{{\rm O}_{\rm 2}}$= –13.8, –14.2 and –15.8, respectively, at 900°C. Recovered spinels were mounted in epoxy, ground, and polished using standard diamond solutions for XANES analysis and EMPA. Individual crystals of each sample were selected for high-quality XRD analysis, and examined optically to ensure absence of twinning and inclusions.
Analytical methods
EMPA
Compositions were determined with a Cameca SX-100 electron microprobe, using an accelerating voltage of 15 KeV, a 20 nA beam current with a 2 µm effective beam diameter. Primary standards and analysing crystals were as follows: Al (Spinel BL8, TAP, 593.6 cps/nA), Mn (Tephroite, LLIF, 247.4 cps/nA), O (Tephroite, PCO, 46.4 cps/nA) and Fe (Fayalite, LLIF, 300.4 cps/nA). Kα lines were used for all analyses. Sample Ga60 was measured using a JEOL JXA8530 F Hyperprobe, at the University of Bristol. Data for this sample were collected with an accelerating voltage of 15 keV, a 10 nA beam current and a 1 µm beam diameter. Primary standards and analysing crystals were as follows: Al (B4 Spinel, TAP), Mn (Mn metal, LLIF) and Fe (Fayalite, LLIF). Transects of larger crystals indicate crystals are chemically homogenous, unzoned in Fe/Mn/Al/O content. However, for some samples, up to 1.2 wt.% standard deviations may suggest some minor compositional variation between crystals from the same run.
X-ray absorption spectroscopy
Beamline I18 at the Diamond Light Source (DLS), Harwell, UK was used to collect Mn K-edge and Fe K-edge XANES spectra. These spectra were acquired in fluorescence geometry, with samples angled at 80° to the incident beam. A Si(111) double crystal monochromator was used to finely tune the energy of the beam, which was focused on the sample with a spot size of 6 µm. Scans were measured over an energy range of 6400–6570 eV for the Mn K-edge and 7000–7320 eV for the Fe K-edge. Step size for Mn XANES scans across the pre-edge peak and main edge region was 0.25 eV. Step size for Fe XANES data was 0.25 eV over the pre-edge peak and 0.3 eV across the edge region. Following data collection, scans were imported into the ATHENA program (Ravel and Newville, Reference Ravel and Newville2005) where spectra were deglitched, aligned, merged, and normalized using standard in-built routines. The Fluo algorithm (Haskel, Reference Haskel1999) was applied to correct for self-absorption. A reference foil of Mn and Fe was used for energy calibration of the monochromator, which was applied to all spectra. The Fe K-edge calibration was set to the first inflection point of the reference foil, set at 7112 eV, and corrected to 7110.75 eV (Kraft et al., Reference Kraft, Stümpel, Becker and Kuetgens1996) for easy comparison with other work. The Mn K-edge calibration was set to the first inflection point in Mn foil, set at 6539 eV and corrected to 6537.67 eV (Kraft et al., Reference Kraft, Stümpel, Becker and Kuetgens1996). The AUTOBK algorithm was used to model and remove the background using a spline fit procedure. Following normalization data were then exported to the Fityk software (Wojdyr, Reference Wojdyr2010) where a convex hull spline fit was used to subtract the background from pre-edge peaks, prior to the fitting of Gaussian peaks.
Single-crystal X-ray diffraction
Crystals of galaxite and jacobsite, observably free of defects and untwinned under a polarized transmitting-light microscope, were selected for SC-XRD experiments at the Dipartimento Scienze della Terra, Università degli Studi di Milano. A preliminary test on the crystal quality was performed using a KUMA KM4 four-circle diffractometer, equipped with a point-detector and a monochromatized MoKα radiation, by the analysis of the profile of the diffraction peaks; samples with poorer observed crystallinity were discounted. Intensity data were then collected using an Oxford Diffraction Xcalibur diffractometer, equipped with a CCD detector and operating at 50 kV and 40 mA, with monochromatized MoKα radiation. A combination of ω scans, with 1° step and 10 s exposure time per frame, was chosen to maximize the redundancy and data coverage. For all the data collections, the reflection conditions agreed with the space group Fd ![]() $\bar 3$m, as expected for galaxite and jacobsite. Intensity data were then integrated and corrected for Lorentz-polarization and absorption effects (by Gaussian integration based upon the physical description of the crystal) using the CrysAlis software package (Agilent, 2012). Further details pertaining to the data collection protocols are given in Table 1.
$\bar 3$m, as expected for galaxite and jacobsite. Intensity data were then integrated and corrected for Lorentz-polarization and absorption effects (by Gaussian integration based upon the physical description of the crystal) using the CrysAlis software package (Agilent, 2012). Further details pertaining to the data collection protocols are given in Table 1.
Table 1: Details pertaining to the X-ray single-crystal structure refinements of the galaxite and jacobsite samples.
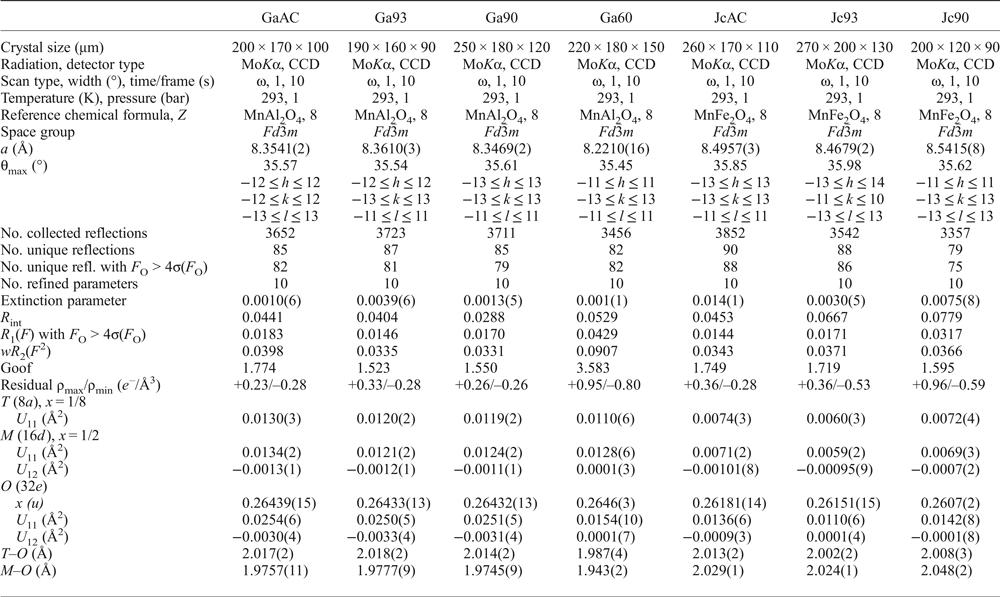
Note: origin fixed at ![]() $\bar 3$m; R int = Σ|F O2 – F O2(mean) |/Σ[ F obs2 ]; R 1(F) = Σ (|F O| – |F C|)/Σ|F O|; wR 2 (F 2) = [Σ [w(F 2O – F 2C)2]/ Σ [w(F 2O)2]]0.5; s.o.f. are given in Table 3, as refined atomic fraction and as electron content per site Σe–.
$\bar 3$m; R int = Σ|F O2 – F O2(mean) |/Σ[ F obs2 ]; R 1(F) = Σ (|F O| – |F C|)/Σ|F O|; wR 2 (F 2) = [Σ [w(F 2O – F 2C)2]/ Σ [w(F 2O)2]]0.5; s.o.f. are given in Table 3, as refined atomic fraction and as electron content per site Σe–.
The anisotropic displacement factor exponent takes the form: –2π2[(ha*)2U 11 +…+ 2hka*b*U 12 +…+2klb*c*U 23].
The anisotropic structural refinements were performed using the SHELX-97 software (Sheldrick, Reference Sheldrick2008) starting from the atomic coordinates of Lucchesi et al. (Reference Lucchesi, Russo and Della Giusta1997). Neutral atomic scattering factors for O, Al, Mn and Fe were taken from the International Tables for Crystallography (Wilson and Prince, Reference Wilson and Prince1999). The site population was modelled with two different protocols for galaxite and jacobsite, respectively, as described below. Secondary isotropic extinction effects were corrected according to the formalism of Larson (Reference Larson1967), as implemented in the SHELXL-97 package. Further details pertaining to the structure refinements are given in Table 1.
Results
Galaxite
The averaged chemical compositions of the synthetic galaxite samples are summarized in Table 2, with Mn valence estimated based on ensuring net neutrality with O2– and Al3+. Samples GaAC, Ga93 and Ga90 all have similar chemical compositions, but are depleted in Al and O compared to stoichiometric galaxite. These three samples are closer in composition to spinels with 2:1 cations of Mn:Al. In contrast, Ga60 has near equal wt.% abundance of Mn and Al and a higher wt.% O than the other samples, with a composition more similar to end-member galaxite with 2:1 cations of Al:Mn.
Table 2: Averaged compositions and element totals of jacobsite and galaxite samples determined by electron microprobe.1
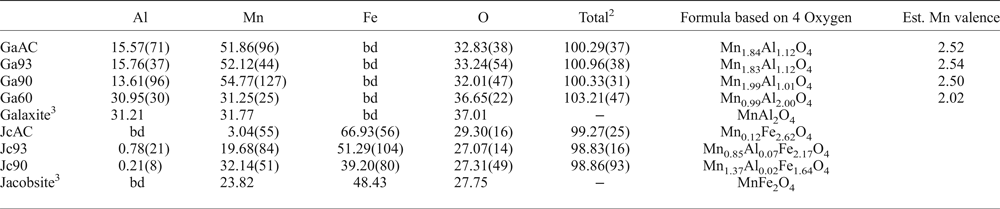
1Figures in parentheses are the standard deviations on the last significant figure of the average value, including element totals.
2Average of the element totals for all analyses.
3Compositions of the ideal end-member.
bd – below detection limits.
Single-crystal XRD refinements for the galaxite samples (i.e. ‘GaAC’, ‘Ga93’, ‘Ga90’, ‘Ga60’, Table 1 and 3) were performed using a mixed Al/Mn- scattering curve at the M and T sites. The fraction of Al and Mn at both M and T sites was refined simultaneously. For all the data sets, convergence was achieved rapidly and the variance–covariance matrix showed no significant correlation between the refined parameters. At the end of all the refinements, the residuals in the difference-Fourier maps of the electron density were less than ±0.3 e –/Å3, with agreement factors R 1(F) < 0.02 (with F O > 4σ(F O) and 10 refined parameters, Table 1). For the sample ‘Ga93’, which showed a lower crystallinity as deduced based on the profile shape of the Bragg peaks, the residuals were ±0.9 e –/Å3, with agreement factors R 1(F) ~ 0.04. Atomic positions, site occupancy factors (s.o.f.), displacement parameters and bond distances are also reported in Tables 1 and 3.
Table 3: SC-XRD refinements for galaxite-group data, and refinement which includes cation distribution based on modelling of bond lengths.

Δ (![]() $\Sigma {e}_{{\rm pfu}}^{\rm \ndash} $.)% is defined as the difference of the total e- number between the structural refinement and the final refinement based on bond-length modelling.
$\Sigma {e}_{{\rm pfu}}^{\rm \ndash} $.)% is defined as the difference of the total e- number between the structural refinement and the final refinement based on bond-length modelling.
Data from XANES of the Mn K-edge for the galaxite samples are shown in Fig. 1. The spectra for GaAC, 93 and 90 are all remarkably similar with a small, less defined shoulder on the rising edge (6551.5 eV), followed by the white line position at ~6557 eV and a slight shoulder at ~6569 eV. In comparison, the Ga60 spectrum has a more intense pre-edge peak, a much more defined peak on the rising shoulder and a more defined peak following the main absorption crest (6569 eV). The lower shoulder position may be associated with the white line peak position of Mn2+, whilst the main absorption peak is associated with Mn3+. This suggests both the presence of Mn2+ and Mn3+ in the galaxite samples. The more intense 1s→3d transition (pre-edge peaks) found in the spectrum for Ga60 suggests a larger proportion of Mn cations on T sites (Chalmin et al., Reference Chalmin, Farges and Brown2009). XANES spectra for these samples lack any characteristic features in the main edge and pre-edge peak region associated with Mn4+. The edge energy, white line position, and pre-edge centroid energy are all at a lower energy in the galaxite samples than their positions in standards with Mn4+ (Farges, Reference Farges2005; Chalmin et al., Reference Chalmin, Farges and Brown2009; Manceau et al., Reference Manceau, Marcus and Grangeon2012) so it was assumed that no Mn4+ was present, although the presence of minor proportions of Mn4+ cannot be dismissed.
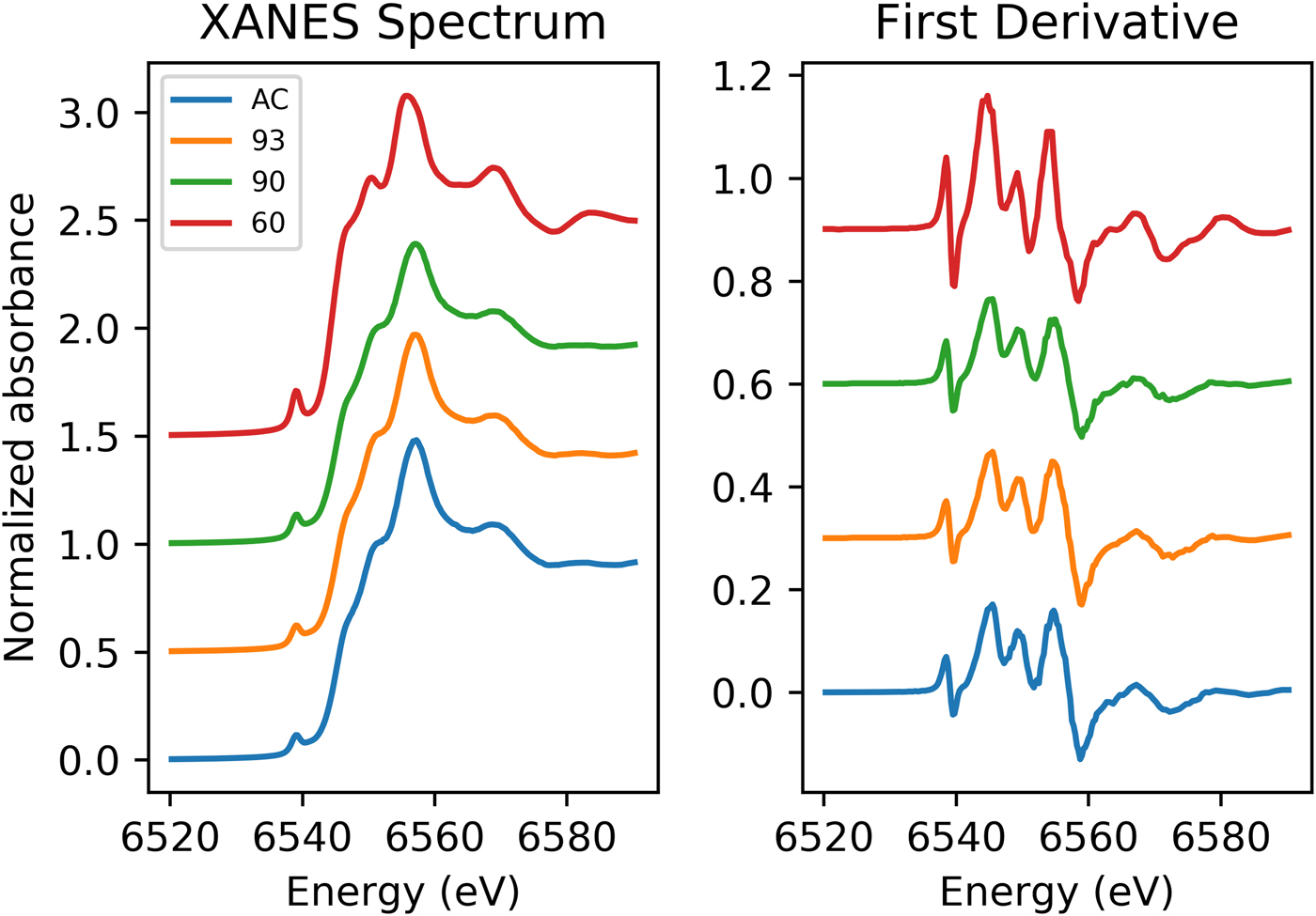
Fig. 1. Normalized Mn K-edge XANES spectra for galaxite samples AC, 93, 90 and 60 (offset vertically for clarity).
Peak fitting of the pre-edge peak for the galaxite samples, following background removal, show that the 1s→3d transition peak can be modelled using one or two Gaussian peaks. The results of fitting are shown in Table 4. The centroid energy for all Galaxite groups are within error of each other, suggesting that the mean valence of Mn in all groups is the same. However, as identified from Fig. 1, the pre-edge peak intensity varies between samples, suggesting that samples GaAC and Ga93 have the least amount of Mn in tetrahedral coordination and Ga60 has the most.
Table 4: Mn K-edge pre-peak data for galaxite and jacobsite samples and Fe K-edge data from jacobsite spectra.
Jacobsite
The averaged EMPA data for the three jacobsite runs (JcAC, Jc93 and Jc90, Table 2) show a decrease in Fe and an increase in Mn under more reducing conditions. Sample JcAC is almost Mn free, and, therefore, is expected to be similar in structure to magnetite (Fe3O4). Samples Jc93 and Jc90 are closer in composition to ideal jacobsite, but Jc93 has excess Fe while Jc90 is deficient in Fe compared to the ideal end-member.
Single-crystal XRD refinements for the jacobsite samples (JcAC, Jc93 and Jc90) were first performed using a mixed Fe/Mn-scattering curve at the octahedral and tetrahedral sites, while the fraction of Fe and Mn at the M and T sites were refined simultaneously. However, the similar X-ray scattering factors of Fe and Mn led to a severe correlation between the refined Fe/Mn site populations. A different strategy was then adopted, where site occupancies were modelled using the scattering curve of Fe alone (i.e. the element with the highest scattering factor). The refined partial site occupancy confirms the presence of a lighter element (i.e. Mn), and the refined e – content per site represents the actual (Fe + Mn) contribution (Table 3). With this protocol, convergence was achieved rapidly on all the data sets, and the variance–covariance matrix showed no significant correlation between the refined parameters. The quality of the refinements of the sample ‘JcAC’ (±0.3 e –/Å3, R 1(F) ~ 0.01) and ‘Jc93’ (±0.5 e –/Å3, R 1(F) ~ 0.02) was slightly better than that of the sample ‘Jc90’ (±0.9 e –/Å3, R 1(F) ~ 0.03; Table 1). Atomic positions, site occupancy factors, displacement parameters and bond distances are also reported in Tables 1 and 3. The crystallographic information files have been deposited with the Principal Editor of Mineralogical Magazine and are available as Supplementary material (see below).
Stacked Fe K-edge XANES spectra for jacobsite samples are shown in Fig. 2. The absorption edge in Jc90 and Jc93 plots between the edge position of Fe3O4 and Fe2O3, suggesting the mean oxidation state of iron may be greater than +2.6 in these samples. The K-edge of JcAC is similar to that of Fe2O3, suggesting the mean valance state is close to +3, as would be expected.
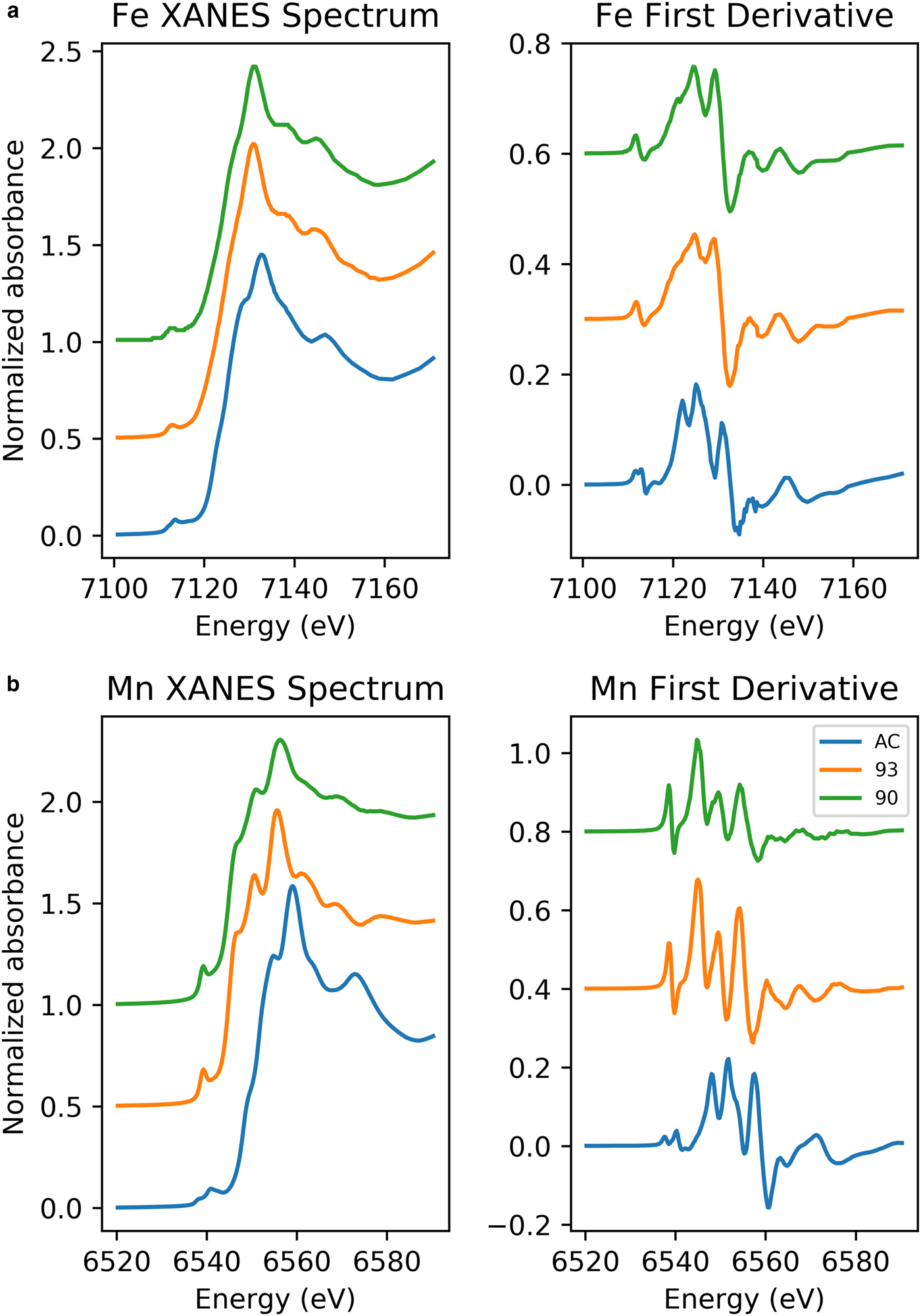
Fig. 2. (a) Fe K-edge XANES spectra of jacobsite spinel synthesized with: 93%, 90% CO2 and no gas flow. (b) Mn K-edge XANES spectra of jacobsite spinel synthesized with: 93% CO2, 90% CO2 and no gas flow.
The number, intensity and centroid position of Gaussian/pseudo-Voight components which can be fitted to the 1s→3d and 1s→4p (quadrupolar and dipolar) electronic transitions that produce the Fe pre-edge feature can be used to extract information on the coordination and average oxidation state of Fe (Waychunas et al., Reference Waychunas, Brown and Apted1983; Westre et al., Reference Westre, Kennepohl, DeWitt, Hedman, Hodgson and Solomon1997; Wilke et al., Reference Wilke, Farges, Petit, Brown and Martin2001). By comparing the Fe pre-edge data to mineral standards where Fe is in a single valence, the average valence of iron can be estimated if it is assumed that there is a linear trend between centroid energy and valence state. Using tabulated values for mineral standards from Wilke et al. (Reference Wilke, Farges, Petit, Brown and Martin2001), Fe oxidation state has been estimated for the jacobsite samples. However, these are only approximations for the Fe redox state, as when redox state and coordination change at the same time there is a considerable non-linearity with redox and centroid position (Wilke et al., Reference Wilke, Farges, Petit, Brown and Martin2001).
Jc90 and Jc93 Fe K-edge pre-edge features can be fitted using two Gaussian functions. The centroid position for these two functions were close to 7112.2 eV and 7113.2 eV. The JcAC spectrum required fitting using four Gaussian functions, with two at ~7113.45 eV and two further peaks with centroid positions greater than 7115 eV, indicating either an environment around Fe which is either tetrahedral or distorted octahedral (Pinakidou et al., Reference Pinakidou, Katsikini, Paloura, Kavouras, Kalogirou, Komninou, Karakostas and Erko2006) or long-range order around Fe involving 3d orbitals of neighbouring iron atoms (Wilke et al., Reference Wilke, Farges, Petit, Brown and Martin2001). Therefore, the third and fourth peak were excluded from calculating the mean centroid position and total integrated area. The pre-edge averaged centroid position (Table 4) was compared to the variation of centroid position with redox ratio of mixtures found in Wilke et al., (Reference Wilke, Farges, Petit, Brown and Martin2001). The estimated Fe3+/∑Fe values were taken for the mixtures of IVFe2+/VIFe3+ which should give the maximum %Fe3+ for a given centroid position. JcAC plots with 98% Fe3+, whilst there is ~74% Fe3+ in samples Jc93, and 70% Fe3+ in Jc90. The integrated pre-edge intensity suggests that sample Jc90 contains greater proportions of Fe on the M site compared to samples Jc93 and JcAC.
The Mn K-edge spectra for the jacobsite samples are shown in Fig. 2b. As with Fe K-edge spectra shown in Fig. 2, samples Jc90 and Jc93 have a similar shape, but different intensities, whereas the JcAC spectrum is shifted towards a higher absorption energy, which suggests Mn in this sample, on average, is in a higher redox state. For samples Jc93 and Jc90 there is a slight peak on the rising edge at ~6551 eV, which corresponds with the white line position of Mn2+ standards, and a further peak with the greatest intensity at 6556 eV, which is slightly lower than the white line position of Mn3+ standards found over the energy range 6557–6559 eV. The pre-edge peak for samples Jc93 and Jc90 can be modelled using three peaks whereas JcAC has to be modelled using more functions. A triplet is suggestive of Mn3+ or Mn4+ being present in the 93 and 90 samples (Farges, Reference Farges2005). The averaged Mn pre-edge peak centroid position is given in Table 4. The intensity of the 1s→3d transition suggests that Jc93 has greater amounts of T coordinated manganese than samples JcAC or Jc90. The energy position of the Mn K-edge for the jacobsite samples suggests that Jc90 and Jc93 consists of a mixture of Mn2+ and Mn3+, and its position close to a MnO standard suggests that 2+ dominates in these samples. Whereas, the edge position of JcAC is greater than Jc93 and Jc90, and is close to the edge position of a Mn2O3 standard, suggestive of Mn in an oxidation state of 3+, or greater.
Discussion
The single-crystal X-ray diffraction data of the galaxite and jacobsite samples provide unit-cell constants and u parameters in agreement with those reported in the literature (e.g. Bosi et al., Reference Bosi, Hålenius, Andreozzi, Skogby and Lucchesi2007; Essene and Peacor, Reference Essene and Peacor1983; Lucchesi et al., Reference Lucchesi, Russo and Della Giusta1997; Hålenius et al., Reference Hålenius, Bosi and Skogby2007). In this class of minerals, the length of the cell edge and the polyhedral bond distances are geometrically related, which in turn reflects the degree of cation ordering among the T and M sites. The structure refinements converged with a ratio of the displacement parameters of the T, M and oxygen sites (i.e. U eq(T):U eq(M):U eq(O)], where U eq is the equivalent isotropic atomic displacement parameter and is defined as a third of the trace of the orthogonalized matrix U ij, which describes the anisotropic displacement ellipsoid) comparable to the literature data for these two spinels. Refined Al/Mn-fractions at the M and T sites in galaxite reflect the actual distribution of the two cations. In contrast, the Fe-fraction at the M and T sites in jacobsite is only ‘virtual’ and reflects the electron content per site due to the co-presence of Fe and Mn. The calculated sum of the electron content at the T and M sites on the basis of the multi-element distribution obtained by the X-ray structure refinements and by bond length modelling/EMPA are given in Table 3. We defined the parameter Δ(![]() $\Sigma {e}_{{\rm pfu}}^{\rm \ndash} $ Z)% as the difference of the total e – number (per formula unit) between the values obtained by the X-ray structure refinements and by bond length modelling/EMPA. This parameter provides an assessment of the consistency between the results obtained by the different experimental methods used here.
$\Sigma {e}_{{\rm pfu}}^{\rm \ndash} $ Z)% as the difference of the total e – number (per formula unit) between the values obtained by the X-ray structure refinements and by bond length modelling/EMPA. This parameter provides an assessment of the consistency between the results obtained by the different experimental methods used here.
Cation distribution in Galaxite
Hålenius et al. (Reference Hålenius, Bosi and Skogby2007) reported a stoichiometric synthetic manganese aluminate (MnAl2O4) which has a partial inverse spinel structure with an inversion parameter, i = 0.1, with Mn2+ strongly ordered on the T site. However, the degree of inversion for other natural and synthetic spinels is likely to be dependent on the method of preparation (Schreyeck et al., Reference Schreyeck, Wlosik and Fuzellier2001; Carta et al., Reference Carta, Casula, Mountjoy and Corrias2008), thermal history (Ball et al., Reference Ball, Pirzada, Grimes, Zacate, Price and Uberuaga2005, Andreozzi et al., Reference Andreozzi, Princivalle, Skogby and Della Giusta2000), as well as the chemical composition of the spinel (Carta et al., Reference Carta, Casula, Falqui, Loche, Mountjoy, Sangregorio and Corrias2009, Andreozzi et al., Reference Andreozzi, Lucchesi, Skogby and Della Giusta2001). Thermodynamic models of cubic spinel in the Al–Mn–O system suggests that a generalized form for this system is (Chatterjee and Jung, Reference Chatterjee and Jung2014):
whereas, in the case of tetragonal Al–Mn–O spinels, Mn2+ and Mn3+ can occupy both the T and M sites. Because the galaxite samples only have one multivalent element, and by assuming that Mn4+ is not present in these samples, the Mn3+/Mn2+ ratio can be calculated from the compositional average point analyses and the SC-XRD data, ensuring net electrical neutrality. Charge balance of the spinel structure can be used in the galaxite samples to determine the proportion of Mn2+ and Mn3+ cations present in each sample (i.e. the average Mn valence). The distribution of these Mn cations can then be established by ensuring the distribution between the M and T sites simultaneously satisfies the following two parameters: (1) the mean atomic number (m.a.n.) for each site, as defined by:
where Xi is the fraction of the cation species in the T and M sites, and Ni is their atomic number; and (2) the polyhedral bond length, calculated from a linear combination of each cation species cation–oxygen bond distances from end-member spinels:
where IVDi and VIDi are the cation to oxygen bond distance of each cation in the T and M sites, respectively.
The X-ray structure refinement data (Table 3) already satisfies equations 3 and 4, so by applying equations 5 and 6, the distribution of Mn2+ and Mn3+ can be determined. The distribution of cations across the T and M sites was calculated using the cation–oxygen bond lengths listed in Table 5. Determining cation distribution is made simpler by first assuming that Mn3+ cations are found on the M sites, because of the strong preference for Mn2+ for the T site (Chatterjee and Jung, Reference Chatterjee and Jung2014). However, it was found that to model Ga60, considerable amounts of Mn3+ were needed on the tetrahedral site (≈0.2 cations pfu) to satisfy the particularly short T–O bond length.
Table 5: Effective cation–oxygen bond length for oxide spinels (after Lavina et al., Reference Lavina, Salviulo and Giusta2002).

The final structural refinement with cation distribution is given in Table 3. When modelling mean T–O and M–O bond lengths, anything <0.02 Å was considered an acceptable fit (Lavina et al., Reference Lavina, Salviulo and Giusta2002). Calculated M–O bond lengths for the distribution of cations, including oxidation state, are in good agreement with the observed values from the SC-XRD data, giving Δ(M–O) ≤ 0.001 Å for all but the Ga60 sample, where Δ(M–O) = 0.007 Å. However, the presence of a large residual for Δ(T–O) for GaAC, Ga93 and Ga90 T–O bond lengths (≤0.025 Å), when using the 2.04 Å IVMn2+ T–O bond length from Lavina et al. (Reference Lavina, Salviulo and Giusta2002) is unsatisfactory. This difference from the observed and predicted size of the T–O bond, in the galaxite samples, may suggest that a correction function is required. Hålenius et al. (Reference Hålenius, Bosi and Skogby2011), suggests the IVMn–O bond length for a fully ordered end-member galaxite is 2.05 Å. Using 2.05 Å for the IVMn2+ T–O bond length lowers the Δ(T–O) residual for GaAC , Ga93 and Ga90 to <0.02 Å. It is likely that the large structural relaxation is linked to cation occupancy on the M site, which not only alters the M–O bond length, but also changes the octahedral angle O–M–O, lengthening the tetrahedral distance (Bosi et al., Reference Bosi, Andreozzi, Hålenius and Skogby2011). Distortion of the octahedral site from cubic to tetragonal symmetry, due to the Jahn-Teller effect, is expected with increasing concentration of Mn3+ in 6-fold coordination. However, an overall lowering of the space group from Fd ![]() $\bar 3$m to I41–/amd is unlikely unless concentrations of VIMn3+ exceed 1.4 atoms pfu (Lucchesi et al., Reference Lucchesi, Russo and Della Giusta1997). Additional terms have to be added to equation 5 to describe the effect that cation speciation, on the octahedral site, has on the T–O bond lengths (Lavina et al., Reference Lavina, Salviulo and Giusta2002).
$\bar 3$m to I41–/amd is unlikely unless concentrations of VIMn3+ exceed 1.4 atoms pfu (Lucchesi et al., Reference Lucchesi, Russo and Della Giusta1997). Additional terms have to be added to equation 5 to describe the effect that cation speciation, on the octahedral site, has on the T–O bond lengths (Lavina et al., Reference Lavina, Salviulo and Giusta2002).
Where the coefficient k 1 is added to account for the effect of cation X z in the M site (where z is an element which alters the O–M–O bond angle).
The inversion parameters for samples GaAC, Ga93 and Ga90 are between 0.154 and 0.18 which is slightly larger than the 0.1 suggested by Hålenius et al. (Reference Hålenius, Bosi and Skogby2007). Whereas the inversion parameter for sample Ga60 is closer to 0.2. Whilst both the synthetic spinels in our study and those in Hålenius et al. (Reference Hålenius, Bosi and Skogby2007) were flux grown in a borax flux at a final temperature of 900°C, our study cooled at a faster rate (12.5°C/hr compared to 4 °C/hr) from peak temperature, did not contain a surplus of Al2O3 to prevent the formation of trivalent manganese, and were synthesized in more oxidized conditions (with the exception of Ga60). Additionally, whilst our samples were fast quenched in water and air, the quenching technique in Hålenius et al. (Reference Hålenius, Bosi and Skogby2007) only mentions runs that were completed with fast cooling to ambient temperature, hence this quenching technique may not preserve initial cation order (or disorder). These differences in experimental procedures may account for the differing inversion factor and galaxite compositions between our study and Hålenius et al. (Reference Hålenius, Bosi and Skogby2007).
Determining the oxidation state of Fe and Mn using XANES, EMPA and SC-XRD
Cation distribution and oxidation information, from the galaxite samples, can be used to compare how satisfactory existing methods of predicting average valence and coordination from XANES spectra compare. Combining EMPA, XANES and SC-XRD data for samples where there is a sufficient difference in the scattering factors of the cations (e.g. galaxite spinels) can satisfactorily determine the structure of a spinel structure. Furthermore, bond-length modelling in these types of samples can be used to assign cations across the T and M sites. However, for spinels where there may be significant oxygen deficiency, cation vacancies and/or the scattering of the cation ions are too similar meaning there are too many variables to correctly assign cation valence distributions across the T and M sites (e.g. manganese ferrites).
The SC-XRD data and stoichiometric calculations of the EMPA data result in slightly different crystal compositions (hence different mean oxidation state) for each galaxite sample. EMPA data suggests the mean valence of Mn in the galaxite samples is 2.51, 2.53, 2.50 and 2, respectively, for samples GaAC, Ga93, Ga90 and Ga60. Whereas, the oxidation state of Mn implied by the SC-XRD data (Table 3) suggests Mn in all samples has an average valence of ≈2.41 (obtained excluding Ga60).
Data from XANES can be used to determine the oxidation state of Mn and Fe. One common method of determining the average valence and coordination of atoms is by examining the pre-edge peak region of XANES spectra. The pre-edge peak is a manifestation of the 1s→3d transition in transitional metals. Fitting this pre-edge provides what is becoming the preferred technique to obtain quantitative data on cation valence and coordination information from XANES spectra. Other features in XANES spectra which give an indication of the oxidation state of the absorbing atom are white line position and/or the position of the absorption edge. However, these features are highly sensitive to local environment and long-range ordering, and so, are not suitable to determine quantitatively mean oxidation state or coordination. Charge balance and bond-length modelling of the SC-XRD data indicates the probable individual cation charges and coordination in the galaxite samples (Table 3). The next step is to identify how well the valence/coordination information from XRD matches those obtained from pre-edge fitting of synchrotron data.
A test of how well Mn K-edge XANES data can be used to determine oxidation state is to compare the centroid position of the pre-edge peak for the galaxite samples (Table 4), where mean oxidation state has been estimated by EMPA or SC-XRD, to the pre-edge peak of samples with known oxidation state. To compare this dataset to other published studies, we first assessed how the centroid position and intensity in single-valence standards collected during this beamline session and a previous session (Bromiley et al., Reference Bromiley, Gatta and Stokes2015) compared to those in Chalmin et al. (Reference Chalmin, Farges and Brown2009). The centroid position of standards in this study and Chalmin et al. (Reference Chalmin, Farges and Brown2009) agreed within ±0.09 eV. However, when comparing the position of the pre-edge peaks for the galaxite samples (where the estimated valence is either 2.41 SC-XRD, or 2.51 EMPA) the centroid position of these samples should be ≈6539.47 eV according to Chalmin et al. (Reference Chalmin, Farges and Brown2009), compared to the measured value of 6539.04 eV (discrepancy of 0.43 eV). This study highlights the current inability to accurately determine the oxidation state/coordination of atoms using the 1s→3d pre-edge peak found on a Mn K-edge XANES spectrum. Part of this difficulty in determining the oxidation state of Mn using the pre-edge peak may be due to the small energy difference in centroid position between Mn2+/Mn3+ (0.35 eV) and Mn3+/Mn4+ (0.55 eV). The way XANES data is processed and fitted may also produce unambiguity in Mn valence.
Pre-edge peak fitting of the Fe K-edge has been successful in evaluating the Fe3+/∑Fe ratio in silicate glass (Berry et al. Reference Berry, O'Neill, Jayasuriya, Campbell and Foran2003; Cottrell et al. Reference Cottrell, Kelley, Lanzirotti and Fischer2009). Calculating the average valence of Fe in minerals remains challenging due to the need to accurately calibrate XANES spectra for each system investigated (Berry et al., Reference Berry, Yaxley, Woodland and Foran2010). Factors limiting the use of XANES in determining the oxidation state of multivalent elements in minerals include: the restricted range of Fe2+ and Fe3+ found in most minerals; the effect of compositional variability and particularly the effect that crystal orientation has on the collected spectra; and the difficulties in background fitting. In many cases, the oxidation state of redox variable elements tends to be quantified by the weak 1s→3d pre-edge, although this edge, and particular spectral backgrounds to pre-edge features, are also sensitive to changes in coordination, site symmetry and composition (Doyle et al., Reference Doyle, Berry, Schofield and Mosselmans2016). Knowing the cation coordination in a sample is vital in determining the oxidation state of an unknown as shown by the variation of centroid position with redox ratio of mixtures found in Wilke et al. (Reference Wilke, Farges, Petit, Brown and Martin2001). A suite of well documented Fe spinels may provide the means to explore and quantify further the effects that Fe oxidation state and coordination have on the shape of a XANES spectrum due to the varying ratio of Fe3+/∑Fe found in many spinels and the different degrees of inversion found in many spinels.
An alternative way to determine Mn redox states from XANES data is linear combination fitting (LCF) of single valence standards with similar structures to the mixed valent sample (Manceau et al., Reference Manceau, Marcus and Grangeon2012; Bromiley et al., Reference Bromiley, Gatta and Stokes2015), where the resulting fit indicates the relative proportions of each oxidation state present in the unknown sample. Linear combination fitting is reliant on the unknown having the absorbing element in similar coordination to the standard. This is problematic in spinels as Fe and Mn in these samples may exist in two different coordination environments with variable distributions between both sites and these elements may also be present in multiple oxidations states in the same or different sites; therefore, it is unlikely that LCF will give accurate results. Furthermore, it is often difficult to acquire well documented standards where each oxidation state of Mn/Fe is present in all necessary coordination environments. As a first approximation, Mn average valence for the galaxite samples was determined by fitting the spectra with a LCF of MnO and Mn2O3 spectra in the region between 6520 and 6570 eV. This resulted in a mean Mn valence of 2.52, 2.51 and 2.55 for samples GaAC, Ga93 and Ga90, respectively, and an average oxidation state of 2.26 for Ga60. These estimated averaged oxidation states are close to those estimated from EMPA (Table 2), with the exception of Ga60, and generally higher than those estimated based on SD-XRD data (Table 3). Therefore, LCF, both estimates higher average Mn valence, and indicates a change in valence in the most reduced sample (Ga60) which is not apparent from other data. LCF of jacobsite samples suggests that the oxidation state of Mn in JcAC is ≈3+, whilst in Jc93 and Jc90 the oxidation state is 2.3 and 2.4 respectively.
Analysis of the full extended X-ray absorption fine structure (EXAFS) spectrum may be an alternate way to determine site occupancies, although this requires ab initio calculations to produce standards by which sample spectra can be compared. Although EXAFS analysis of jacobsite has been carried out by various groups (Yang et al., Reference Yang, Harris, Calvin, Zuo and Vittoria2004; Kodre et al., Reference Kodre, Arcon, Padeznik Gomilsek and Makovec2008; Carta et al., Reference Carta, Casula, Falqui, Loche, Mountjoy, Sangregorio and Corrias2009) it remains uncertain as to whether this procedure could be used for more complex solid solutions.
Cation distribution in Mn spinel as a function of  $f_{{\rm O}_{\rm 2}}$
$f_{{\rm O}_{\rm 2}}$
Single-crystal XRD refinements from individual galaxite crystals suggest a decrease in TMn2+ and MMn3+ with a reduction in oxygen fugacity, whilst Al3+ (M site and T site) and Mn2+ (M site) increase. These SC-XRD findings are in contrast to the EMPA data which suggest there should be a slight decrease in Al cations pfu with more reduced conditions. The trend difference between these two sets of data may be due in part to EMPA data being measured on multiple crystals whereas SC-XRD data was measured on an individual crystal from a batch, selected based on size and lack of twinning.
Data from EMPA of jacobsite samples suggests that oxygen fugacity affects partitioning of Mn and Fe between the sodium tetraborate flux and spinel crystals, such that total Mn content in spinel increases, and Fe content decreases, with more reducing conditions. This contrasts with the Log ![]() $f_{{\rm O}_{\rm 2}}$-temperature diagram from Bonsdorf et al. (Reference Bonsdorf, Schäfer, Teske, Langbein and Ullmann1998) that would suggest that Fe-rich spinel should dominate under more reduced conditions. The progressive enrichment of Mn-rich spinels with lowering
$f_{{\rm O}_{\rm 2}}$-temperature diagram from Bonsdorf et al. (Reference Bonsdorf, Schäfer, Teske, Langbein and Ullmann1998) that would suggest that Fe-rich spinel should dominate under more reduced conditions. The progressive enrichment of Mn-rich spinels with lowering ![]() $f_{{\rm O}_{\rm 2}}$ in this study, compared to Bonsdorf et al. (Reference Bonsdorf, Schäfer, Teske, Langbein and Ullmann1998), may highlight an effect of different routes of synthesis. An additional effect of reduction for the jacobsite spinels is a decrease in the estimated valence of Fe from ~3+ to ~2.7+ between samples AC and 93/90. Also, there is a significant lengthening of the M–O bonds between samples AC/93 and 90 which would indicate the replacement of Fe3+/Mn3+ with Mn2+/Fe2+. Yamanaka and Nakahira (Reference Yamanaka and Nakahira1973) noted that a decrease in
$f_{{\rm O}_{\rm 2}}$ in this study, compared to Bonsdorf et al. (Reference Bonsdorf, Schäfer, Teske, Langbein and Ullmann1998), may highlight an effect of different routes of synthesis. An additional effect of reduction for the jacobsite spinels is a decrease in the estimated valence of Fe from ~3+ to ~2.7+ between samples AC and 93/90. Also, there is a significant lengthening of the M–O bonds between samples AC/93 and 90 which would indicate the replacement of Fe3+/Mn3+ with Mn2+/Fe2+. Yamanaka and Nakahira (Reference Yamanaka and Nakahira1973) noted that a decrease in ![]() $f_{{\rm O}_{\rm 2}}$ resulted in a decrease in the lattice parameter with
$f_{{\rm O}_{\rm 2}}$ resulted in a decrease in the lattice parameter with ![]() $f_{{\rm O}_{\rm 2}}$, whereas, in this study, the most reduced sample has the largest lattice parameter. Differences between this study and Yamanaka and Nakahira (Reference Yamanaka and Nakahira1973) may be because their experiments were carried out using solid-state reactions whereas here mineral composition is not nominally fixed but varies as a function of the behaviour of the borax flux.
$f_{{\rm O}_{\rm 2}}$, whereas, in this study, the most reduced sample has the largest lattice parameter. Differences between this study and Yamanaka and Nakahira (Reference Yamanaka and Nakahira1973) may be because their experiments were carried out using solid-state reactions whereas here mineral composition is not nominally fixed but varies as a function of the behaviour of the borax flux.
The oxygen fugacity for runs Ga93/Jc93 and Ga90/Jc90 equates to IW +2.5 and +2.9 respectively. These values span ![]() $f_{{\rm O}_{\rm 2}}$ ranges which are expected for Martian rocks (e.g. nahklites and chassingnites – Wadhwa, Reference Wadhwa and MacPherson2008; Righter et al., Reference Righter, Sutton, Danielson, Pando and Newville2016) as well as primitive basaltic rocks found on Earth (Righter et al., Reference Righter, Sutton, Danielson, Pando and Newville2016). The coupled variation of Fe and Mn found in the jacobsite samples run at IW +2.5 and +2.9 could have potential for helping to constrain the redox conditions of Martian and terrestrial basalts with further study.
$f_{{\rm O}_{\rm 2}}$ ranges which are expected for Martian rocks (e.g. nahklites and chassingnites – Wadhwa, Reference Wadhwa and MacPherson2008; Righter et al., Reference Righter, Sutton, Danielson, Pando and Newville2016) as well as primitive basaltic rocks found on Earth (Righter et al., Reference Righter, Sutton, Danielson, Pando and Newville2016). The coupled variation of Fe and Mn found in the jacobsite samples run at IW +2.5 and +2.9 could have potential for helping to constrain the redox conditions of Martian and terrestrial basalts with further study.
This study suggests that there may be an observable change in the partitioning of Mn between Mn–Fe–O spinel and silicate melt. A recent study by Wijbrans et al. (Reference Wijbrans, Klemme, Berndt and Vollmer2015), on the influence of composition and oxygen fugacity on spinel-melt partitioning, found that Mn is slightly incompatible in spinel. They noted no observable effect on the partitioning of Mn with redox and change in temperature, but did observe a slight compositional effect, with higher partition coefficients for Mn in Fe2+-rich spinels compared to Mg-rich spinels. This further indicates the complex interplay between partitioning behaviour, site occupancy, site distortion, and crystal chemistry in spinel-group minerals. As such, although investigation of end-member compositions may provide insight into the distribution and ordering of multi-valent elements in spinels, data cannot readily be applied to modelling the effects of external influences such as ![]() $f_{{\rm O}_{\rm 2}}$ on the valence state of Fe, and in particular, Mn.
$f_{{\rm O}_{\rm 2}}$ on the valence state of Fe, and in particular, Mn.
Concluding remarks
Manganese- and iron-bearing spinels may have the potential to determine ![]() $f_{{\rm O}_{\rm 2}}$ conditions for the parental melt they formed, by recording the effects of
$f_{{\rm O}_{\rm 2}}$ conditions for the parental melt they formed, by recording the effects of ![]() $f_{{\rm O}_{\rm 2}}$ on element distribution (partitioning and site ordering). This may be due to lengthening of the M–O bond length in sample Jc90 which may result from a change in the cation oxidation state or species on the M site under more reducing
$f_{{\rm O}_{\rm 2}}$ on element distribution (partitioning and site ordering). This may be due to lengthening of the M–O bond length in sample Jc90 which may result from a change in the cation oxidation state or species on the M site under more reducing ![]() $f_{{\rm O}_{\rm 2}}\hskip -2pt$. However, decoupling the effects of temperature and oxygen fugacity on TFe3+–TMn2+ exchange in jacobsite spinels is non-trivial. Furthermore, determining the mean oxidation state and coordination environment of Fe and Mn in spinels using XANES remains challenging if both the oxidation state and coordination of the absorbing atom changes between samples and standards. Additional insight into spinel crystal chemistry can be provided by comparing results of compositional analyses, XANES and SC-XRD refinements, although difficulties in modelling Mn XANES spectra mean that this approach is better suited to constraining the crystal chemistry of end-member compositions, rather than complex, naturally occurring spinels. In contrast to jacobsite, Mn content in galaxite spinels shows little if not no change with varying oxidation conditions of synthesis, implying that element partitioning in spinel is compositionally and structurally dependent. This indicates that variation in Mn valence in spinel is largely driven by changes in Fe valence, presumably via the exchange Mn2+ + Fe3+ ⇌ Mn3+ + Fe2+.
$f_{{\rm O}_{\rm 2}}\hskip -2pt$. However, decoupling the effects of temperature and oxygen fugacity on TFe3+–TMn2+ exchange in jacobsite spinels is non-trivial. Furthermore, determining the mean oxidation state and coordination environment of Fe and Mn in spinels using XANES remains challenging if both the oxidation state and coordination of the absorbing atom changes between samples and standards. Additional insight into spinel crystal chemistry can be provided by comparing results of compositional analyses, XANES and SC-XRD refinements, although difficulties in modelling Mn XANES spectra mean that this approach is better suited to constraining the crystal chemistry of end-member compositions, rather than complex, naturally occurring spinels. In contrast to jacobsite, Mn content in galaxite spinels shows little if not no change with varying oxidation conditions of synthesis, implying that element partitioning in spinel is compositionally and structurally dependent. This indicates that variation in Mn valence in spinel is largely driven by changes in Fe valence, presumably via the exchange Mn2+ + Fe3+ ⇌ Mn3+ + Fe2+.
The reason for non-stoichiometry in the samples remains unclear. Only the most reduced galaxite sample is close to stoichiometric; samples that have been more oxidized are Al-deficient and Mn-rich. Unlike the findings of Bosi et al. (Reference Bosi, Hålenius, Andreozzi, Skogby and Lucchesi2007) on Mg–Mn–Al spinels, we see no increase in trivalent Mn on the T site with more oxidized conditions based on bond-length modelling (Table 3). XANES data indicate that valence of Mn is substantially higher than 2 in the oxidized samples. This might be explained by the observed relative partitioning of Mn2+ onto the T site; Mn3+ is more readily incorporated onto the M site, where it competes with Al3+. As a consequence, more oxidized samples are more Mn-rich. In Ga60, more reducing conditions favour Mn2+, and therefore, galaxite compositions are close to stoichiometric. SC-XRD data are consistent with an increase in the proportion of TMn in Ga60, although a substantial change in average Mn valence is not observed in XANES data; in fact, it is likely that XANES data do not reveal any change in Mn valence across the galaxite samples.
Redox conditions used during synthesis imply JcAC should contain only Fe3+, consistent with XANES data, and that Fe should be mixed valence in Jc93 and Jc90. Trends in determined Fe average valence are consistent with imposed ![]() $f_{{\rm O}_{\rm 2}}$ conditions. According to the exchange Mn2+ + Fe3+ ⇌ Mn3+ + Fe2+, an increase in the proportion of Fe2+ should result in an increase in the proportion of Mn3+. However, between samples Jc93 and Jc90 there are no obvious changes in the Mn K-edge spectra suggestive of an increase in Mn valence. A decrease in
$f_{{\rm O}_{\rm 2}}$ conditions. According to the exchange Mn2+ + Fe3+ ⇌ Mn3+ + Fe2+, an increase in the proportion of Fe2+ should result in an increase in the proportion of Mn3+. However, between samples Jc93 and Jc90 there are no obvious changes in the Mn K-edge spectra suggestive of an increase in Mn valence. A decrease in ![]() $f_{{\rm O}_{\rm 2}}$ for jacobsite samples results in an increase in Mn contents and decrease in Fe contents. In contrast to galaxite, stoichiometric jacobsite appears to form at intermediate
$f_{{\rm O}_{\rm 2}}$ for jacobsite samples results in an increase in Mn contents and decrease in Fe contents. In contrast to galaxite, stoichiometric jacobsite appears to form at intermediate ![]() $f_{{\rm O}_{\rm 2}}$ conditions. Again, it is unclear what the driving force for this compositional change might be. However, it is logical that stoichiometric jacobsite is stable under intermediate redox conditions, as it nominally contains Mn2+ and Fe3+. Under more reducing conditions, the average valence of Fe decreases. Partially disordered jacobsite can form a partial solid-solution series with magnetite, Fe2+Fe3+2O4, which has an inverse spinel structure. As such, the 3+ Fe is expected to readily substitute onto the T site in jacobsite. The observed preference for Mn2+ to be incorporated onto the T site in spinels would, in combination with the ability for Fe to be incorporated onto either site, explain why jacobsite samples here are non-stoichiometric and Fe-rich. Under the most reduced conditions under which jacobsite is stable (i.e. Jc90), crystals become in turn non-stoichiometric and Mn-rich. This might again relate to an increase in proportion of Mn2+, although this remains unsupported by XANES data.
$f_{{\rm O}_{\rm 2}}$ conditions. Again, it is unclear what the driving force for this compositional change might be. However, it is logical that stoichiometric jacobsite is stable under intermediate redox conditions, as it nominally contains Mn2+ and Fe3+. Under more reducing conditions, the average valence of Fe decreases. Partially disordered jacobsite can form a partial solid-solution series with magnetite, Fe2+Fe3+2O4, which has an inverse spinel structure. As such, the 3+ Fe is expected to readily substitute onto the T site in jacobsite. The observed preference for Mn2+ to be incorporated onto the T site in spinels would, in combination with the ability for Fe to be incorporated onto either site, explain why jacobsite samples here are non-stoichiometric and Fe-rich. Under the most reduced conditions under which jacobsite is stable (i.e. Jc90), crystals become in turn non-stoichiometric and Mn-rich. This might again relate to an increase in proportion of Mn2+, although this remains unsupported by XANES data.
Combining XANES and SC-XRD data can be used to create a new series of mixed valent and mixed coordination standards for further studies. Future standards could include spinels such as galaxite where there is less ambiguity in the final refined structure than jacobsite. For jacobsite, the similar scattering of Fe and Mn makes correct valence and coordination assignment much more difficult without additional data such as Mössbauer or neutron-diffraction data. Additionally, the relationship between composition, site occupancy and Fe and Mn valence in spinels is complex and interdependent. As such, development of an oxy-barometer based on spinel crystal chemistry is non-trivial.
Acknowledgements
The authors acknowledge the experimental and analytical facilities at The University of Edinburgh, The University of Milan and The University of Bristol. We thank Chris Hayward and Benjamin Buse for assistance with EMP analyses, Diamond Light Source for access to beamline I18 (Sp10070), and Fred Mosselmans for assistance with XANES measurements. This work was funded by a NERC DTP grant (Grant award code NE/L002558/1).
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1180/mgm.2018.109.