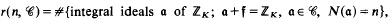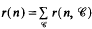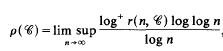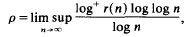Research Article
Some explicit continued fraction expansions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
-
- Article
- Export citation
A note on lattices of rational functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-13
-
- Article
- Export citation
On some applications of formulae of Ramanujan in the analysis of algorithms
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-33
-
- Article
- Export citation
A note on asymmetric approximation
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 34-41
-
- Article
- Export citation
On the space of continuous functions on a dyadic set
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-49
-
- Article
- Export citation
Distributions de signes
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-62
-
- Article
- Export citation
The rotation of two circular cylinders in a viscous fluid
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-66
-
- Article
- Export citation
Wave-source expansions for water of infinite depth in the presence of surface tension
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-76
-
- Article
- Export citation
Completely right pure monoids: the general case
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-88
-
- Article
- Export citation
Mosco convergence and weak topologies for convex sets and functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-104
-
- Article
- Export citation
Slice discrepancy and irregularities of distribution on spheres
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-116
-
- Article
- Export citation
Centrally symmetric convex bodies and Radon transforms on higher order Grassmannians
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-133
-
- Article
- Export citation
Irreducible convex sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 134-155
-
- Article
- Export citation
Some infinite families of satellite knots with given Alexander polynomial
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 156-169
-
- Article
- Export citation
On the distribution of apk modulo one
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 170-184
-
- Article
- Export citation
On the number of integral ideals of given norm and ray-class
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-190
-
- Article
- Export citation
A note on radial variation of analytic functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-193
-
- Article
- Export citation
Book Review
J. Adamek, H. Herrlich and G. Strecker. Abstract and Concrete Categories. Wiley. 1990, 482 pp., £43–65. - A. D. Alexandrov and Y. G. Reshetnyak. General Theory of Irregular Curves. Kluwer Academic. 1989, 288 pp., £66. - V. I. Arnold. Huygens and Barrow, Newton and Hooke: Pioneers in Mathematical Analysis and Catastrophe Theory from Evolvents to Quasicrystals. Birkhäuser. 1990, 118 pp., Swiss Franks 24. - A. C. Baker and H. L. Porteous. Linea Algebra and Differential Equations. Ellis Horwood. 1990, 390 pp., £19-95. - G. Burns and A. M. Glazer. Space Groups for Solid State Scientists. 2nd Edition. Academic Press. 1990, 343 pp., $39.95. - A. Chakrabarti. Elements of Ordinary Differential Equations and Special Functions. Wiley. 1990, 148 pp., £24-50. - L. de Branges, I. Gohberg and J. Rovnyak. SeeI. Gohberg. - L. Debnath and P. Mikusinski. Introduction to Hilbert Spaces with Applications. Academic Press. 1990, 509 pp., $49.95. - M. Dozzi. Stochastic Processes with a Multidimensional Parameter. Longman. 1989, 198 pp., £15-50. - R. Durrett. Probability: Theory and Examples. Wadsworth … Brooks/Cole. 1991, 449 pp., £36. - G. Eason and R. W. Ogden. Editors. Elasticity: Mathematical Methods and Applications. Ellis Horwood. 1990, 412 pp., £60. - R. A. Fisher. Statistical Methods, Experimental Design and Scientific Inference. Oxford University Press. 1990, 800 pp., £25. - A. T. Fomenko. The Plateau Problem: Part I Historical survey; Part II The Present State of the Theory. Two volumes. Gordon and Breach. 1990, 220 pp. and 251 pp., $245 for the set. - D. H. Fowler. The Mathematics of Plato's Academy: A New Reconstruction. Clarendon Press. 1991, 401 pp., paper-back £20. - P. B. Garrett. Holomorphic Hilbert Modular Forms. Wadsworth and Brooks/Cole. 1989, 304 pp., £37-50. - R. P. Gilbert and H. C. Howard. Ordinary and Differential Equations with Applications. Ellis Horwood. 1990, 613 pp., £45. - I. Gohberg. Editor. Extension and Interpolation of Linear Operators. Operator Theory: Advances and Applications, Vol. 47. Birkhauser. 1990, 305 pp., Swiss Franks 88. - L. De Branges, I. Gohberg and J. Rovnyak. Editors. Topics in Operator Theory. Operator Theory: Advances and Applications, Vol. 48. Birkhauser. 1990, 448 pp., Swiss Franks 118. - J. R. Hanna and J. H. Rowland. Fourier Series, Transforms and Boundary Value Problems. 2nd Edition. Wiley. 1990, 354 pp., £43. - N. Hartsfield and G. Ringel. Pearls in Graph Theory: A Comprehensive Introduction. Academic Press. 1990, 246 pp., $29.95. - R. F. Hoskins. Standard and Non-Standard Analysis. Ellis Horwood. 1990, 269 pp., £39-95. - I. D. Huntley and D. J. G. James. Editors. Mathematical Modelling. A Source Book of Case Studies. Oxford University Press. 1990, 462 pp., £37-50. - G. Iooss and D. D. Joseph. Elementary Stability and Bifurcation Theory. 2nd edition. Springer. 1989, 324 pp., DM 108. - J. Lutzen. Joseph Liouville, 1809-1882; Master of Pure and Applied Mathematics. Springer. 1990, 884 pp., £81-50. - R. E. Mickens. Difference Equations: Theory and Applications. 2nd edition. Van Nostrand … Reinhold. 1990, 448 pp., £28-50. - G. J. Murphy. C-Algebras and Operator Theory. Academic Press. 1990, 286 pp., $44.50. - A. L. Onishchik and E. B. Vinberg. Lie Groups and Algebraic Groups. Springer, 1990, 328 pp., DM 128. - H. A. Priestley. Introduction to Complex Analysis. Revised Edition. Clarendon Press. 1990, 214 pp., £12-95. - J. T. Sandefur. Discrete Dynamical Systems, Theory and Applications. Clarendon Press. 1990, 445 pp., £16-50. - S. R. Simanca. Pseudo-Differential Operators. Pitman Research Notes in Mathematics No. 236. Longman. 1990, 123 pp., £14. - B. D. Sleeman and R. J. Jarvis. Editors. Ordinary and Partial Differential Equations. Volume II. Longman. 1989, 227 pp., £20. - J. C. Strikwerda. Finite difference schemes and partial differential equations. Wads worth … Brooks/Cole. 1989, 386 pp., £36. - K. Subrahmaniam. A Primer in Probability. Second Edition. Marcel Dekker. 1990, 336 pp., $45. - M. Toda. Non-linear waves and solitons. Kluwer Academic. 1989, 371 pp., £86. - Xiang-qun Yang. The construction theory of denumerable Markov processes. Wiley. 1990, 395 pp., £45.
-
- Published online by Cambridge University Press:
- 07 April 2017, pp. 194-201
-
- Article
- Export citation
Front matter
MTK volume 38 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation



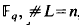 ,
, 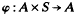 A such that (φ,1)φ and (a, st)φ = ((a, s) t)φ for all a є A and for all s, t є S. We shall refer to right
A such that (φ,1)φ and (a, st)φ = ((a, s) t)φ for all a є A and for all s, t є S. We shall refer to right 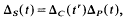
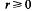 is the linking number of
is the linking number of