Research Article
On Hua's estimates for exponential sums
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-123
-
- Article
- Export citation
Additive Diophantine inequalities with mixed powers I
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 124-130
-
- Article
- Export citation
Additive Diophantine inequalities with mixed powers II
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-140
-
- Article
- Export citation
Seminormal rings generated by algebraic integers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-154
-
- Article
- Export citation
An extension theorem for convex functions and an application to Teicher's characterization of the normal distribution
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-159
-
- Article
- Export citation
T-invariant algebras on Riemann surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 160-171
-
- Article
- Export citation
Construction of polynomials on a number of pseudoconvex domains
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 172-177
-
- Article
- Export citation
A note on the Jeffery paradox
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-186
-
- Article
- Export citation
On the asymptotic properties of linear differential equations
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 187-198
-
- Article
- Export citation
Multiplicative functions on arithmetic progressions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 199-206
-
- Article
- Export citation
Spherical averages of Fourier transforms of measures with finite energy; dimensions of intersections and distance sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-228
-
- Article
- Export citation
Maximally symmetric polyhedral realizations of Dyck's regular map
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-236
-
- Article
- Export citation
A maximally symmetric polyhedron of genus 3 with 10 vertices
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 237-242
-
- Article
- Export citation
Internal characterization of fragmentable spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 243-257
-
- Article
- Export citation
Radon-Nikodým compact spaces and fragmentability
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 258-281
-
- Article
- Export citation
Book Reviews
Book Reviews - I. Anderson. Combinatorics of Finite Sets. Oxford University Press. 1987, 250 pp., £22·50. - M. F. Atiyah et al., Editors. Vector bundles on algebraic varieties. Papers presented at the Bombay Colloquium, 1984. Oxford University Press. 1987, 555 pp., £22·50. - A. Borel et al. Algebraic D-modules. Academic Press. 1987, 355 pp., £25. - P. Blass and J. Lang, Editors. Zariski Surfaces and Differential Equations in Characteristic p > 0. M. Dekker. 1987, 441 pp., $95·50. - D. E. Cohen. Computability and Logic. Ellis Horwood. 1987, 243 pp., £36·50. - R. J. Daverman. Decomposition of Manifolds. Academic Press. 1986, 317 pp., £46. - G. Faltings, G. Wüstholz et al. Rational Points. Seminar Bonn/Wupperial 1983/84. F. Vieweg. 1986, 286 pp., £16·75. - W. Fulton and S. Lang. Riemann-Roch Algebra. Grundlehren d. Math. Wiss., 277. Springer. 1985, 203 pp., DM 158. - A. E. Gelfand, Editor. Contributions to the Theory and Applications of Statistics: A Volume in Honor of Herbert Solomon. Academic Press. 1987, 544 pp., $59·95. - L. J. Gerstein. Discrete Mathematics and Algebraic Structures. W. H. Freeman. 1987, 413 pp., £32·95. - F. Guaraldo, P. Macri and A. Tancredi. Topics on Real Analytic Spaces. Advanced Lectures in Mathematics. Vieweg. 1986, 163 pp., £16·40. - J. C. Jantzen. Representations of Algebraic Groups. Academic Press. 1987, 443 pp., $59.50. - G. S. Ladde, V. Lakshmikantham and B. G. Zhang. Oscillation Theory of Differential Equations with Deviating Arguments. M. Dekker. 1987, 308 pp., $107·50. - Leonardo Pisano Fibonacci. The Book of Squares. Academic Press. 1987, 124 pp., $19·95 or £17. - R. N. McKenzie, G. F. McNutty and W. F. Taylor. Algebras, Lattices, Varieties. Vol. 1. Wadsworth & Brooks/Cole. 1987, 361 pp., $44·95. - J. S. Milne. Arithmetic Duality Theorems. Academic Press. 1986, 421 pp., £32. - C. Năstăsescu and F. van Oystaeyen. Dimensions of Ring Theory. D. Reidel. 1987, 360 pp., £59. - J. Pöschel and E. Trubowitz. Inverse Spectral Theory. Academic Press. 1987, 192 pp., $29·95. - H.-J. Schmeisser and H. Triebel. Topics in Fourier Analysis and Function Spaces. J. Wiley. 1987, 300 pp., £23·95. - I. N. Stewart and D. O. Tall. Algebraic Number Theory. 2nd edition. Chapman & Hall. 1987, 262 pp., £9·95. - D. S. G. Stirling. Mathematical Analysis: a fundamental and straightforward approach. Ellis Horwood. 1987, 172 pp., £9·95. - D. Stoyan, W. S. Kendall and J. Mecke. Stochastic Geometry and its Applications. J. Wiley. 1987, 345 pp., £23.50. - R. A. Usmani. Applied Linear Algebra. Marcel Dekker. 1987, 258 pp., $47·50.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 282-286
-
- Article
- Export citation
Index
Index to Volume 34
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 287
-
- Article
- Export citation
Front matter
MTK volume 34 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation




 .
. 
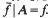 .
.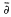 -equation. This, in turn, can be used, analogously to the Cauchy transform on the plane, to develop meromorphic (rational) approximation theory. We sketch the path of the development but omit most of the details when they are very much similar to the planar case. Our presentation follows closely that of [7]. The original motivation for this study was to obtain more information on Gleason parts useful in the study of Carleman (tangential) approximation theory (see [5]).
-equation. This, in turn, can be used, analogously to the Cauchy transform on the plane, to develop meromorphic (rational) approximation theory. We sketch the path of the development but omit most of the details when they are very much similar to the planar case. Our presentation follows closely that of [7]. The original motivation for this study was to obtain more information on Gleason parts useful in the study of Carleman (tangential) approximation theory (see [5]).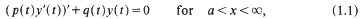
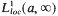 with
with 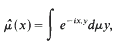
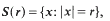
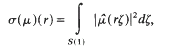
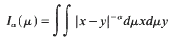
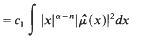
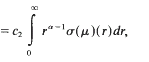
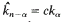 where
where 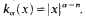 .
.