Article contents
THE STEKLOV SPECTRUM OF CUBOIDS
Published online by Cambridge University Press: 06 December 2018
Abstract
The paper is concerned with the Steklov eigenvalue problem on cuboids of arbitrary dimension. We prove a two-term asymptotic formula for the counting function of Steklov eigenvalues on cuboids in dimension 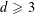 $d\geqslant 3$. Apart from the standard Weyl term, we calculate explicitly the second term in the asymptotics, capturing the contribution of the
$d\geqslant 3$. Apart from the standard Weyl term, we calculate explicitly the second term in the asymptotics, capturing the contribution of the 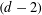 $(d-2)$-dimensional facets of a cuboid. Our approach is based on lattice counting techniques. While this strategy is similar to the one used for the Dirichlet Laplacian, the Steklov case carries additional complications. In particular, it is not clear how to establish directly the completeness of the system of Steklov eigenfunctions admitting separation of variables. We prove this result using a family of auxiliary Robin boundary value problems. Moreover, the correspondence between the Steklov eigenvalues and lattice points is not exact, and hence more delicate analysis is required to obtain spectral asymptotics. Some other related results are presented, such as an isoperimetric inequality for the first Steklov eigenvalue, a concentration property of high frequency Steklov eigenfunctions and applications to spectral determination of cuboids.
$(d-2)$-dimensional facets of a cuboid. Our approach is based on lattice counting techniques. While this strategy is similar to the one used for the Dirichlet Laplacian, the Steklov case carries additional complications. In particular, it is not clear how to establish directly the completeness of the system of Steklov eigenfunctions admitting separation of variables. We prove this result using a family of auxiliary Robin boundary value problems. Moreover, the correspondence between the Steklov eigenvalues and lattice points is not exact, and hence more delicate analysis is required to obtain spectral asymptotics. Some other related results are presented, such as an isoperimetric inequality for the first Steklov eigenvalue, a concentration property of high frequency Steklov eigenfunctions and applications to spectral determination of cuboids.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2018
Footnotes
Current address: Department of Mathematics, University College London, Gower Street, London WC1E 6BT, U.K. email j.lagace@ucl.ac.uk
References
- 7
- Cited by


