Article contents
THE ROBUSTNESS OF EQUILIBRIA ON CONVEX SOLIDS
Published online by Cambridge University Press: 19 December 2013
Abstract
We examine the minimal magnitude of perturbations necessary to change the number 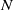 $N$ of static equilibrium points of a convex solid
$N$ of static equilibrium points of a convex solid 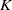 $K$. We call the normalized volume of the minimally necessary truncation robustness and we seek shapes with maximal robustness for fixed values of
$K$. We call the normalized volume of the minimally necessary truncation robustness and we seek shapes with maximal robustness for fixed values of 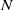 $N$. While the upward robustness (referring to the increase of
$N$. While the upward robustness (referring to the increase of 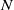 $N$) of smooth, homogeneous convex solids is known to be zero, little is known about their downward robustness. The difficulty of the latter problem is related to the coupling (via integrals) between the geometry of the hull
$N$) of smooth, homogeneous convex solids is known to be zero, little is known about their downward robustness. The difficulty of the latter problem is related to the coupling (via integrals) between the geometry of the hull 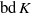 $\mathrm{bd} \hspace{0.167em} K$ and the location of the center of gravity
$\mathrm{bd} \hspace{0.167em} K$ and the location of the center of gravity 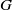 $G$. Here we first investigate two simpler, decoupled problems by examining truncations of
$G$. Here we first investigate two simpler, decoupled problems by examining truncations of 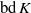 $\mathrm{bd} \hspace{0.167em} K$ with
$\mathrm{bd} \hspace{0.167em} K$ with 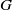 $G$ fixed, and displacements of
$G$ fixed, and displacements of 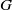 $G$ with
$G$ with 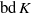 $\mathrm{bd} \hspace{0.167em} K$ fixed, leading to the concept of external and internal robustness, respectively. In dimension 2, we find that for any fixed number
$\mathrm{bd} \hspace{0.167em} K$ fixed, leading to the concept of external and internal robustness, respectively. In dimension 2, we find that for any fixed number 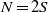 $N= 2S$, the convex solids with both maximal external and maximal internal robustness are regular
$N= 2S$, the convex solids with both maximal external and maximal internal robustness are regular 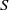 $S$-gons. Based on this result we conjecture that regular polygons have maximal downward robustness also in the original, coupled problem. We also show that in the decoupled problems, three-dimensional regular polyhedra have maximal internal robustness, however, only under additional constraints. Finally, we prove results for the full problem in the case of three-dimensional solids. These results appear to explain why monostatic pebbles (with either one stable or one unstable point of equilibrium) are found so rarely in nature.
$S$-gons. Based on this result we conjecture that regular polygons have maximal downward robustness also in the original, coupled problem. We also show that in the decoupled problems, three-dimensional regular polyhedra have maximal internal robustness, however, only under additional constraints. Finally, we prove results for the full problem in the case of three-dimensional solids. These results appear to explain why monostatic pebbles (with either one stable or one unstable point of equilibrium) are found so rarely in nature.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2013
References
- 3
- Cited by




