Article contents
REPRESENTING AN ELEMENT IN 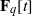 ${\mathbf{F} }_{q} [t] $ AS THE SUM OF TWO IRREDUCIBLES
${\mathbf{F} }_{q} [t] $ AS THE SUM OF TWO IRREDUCIBLES
Published online by Cambridge University Press: 23 May 2013
Abstract
A monic polynomial in 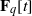 ${\mathbf{F} }_{q} [t] $ of degree
${\mathbf{F} }_{q} [t] $ of degree  $n$ over a finite field
$n$ over a finite field 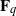 ${\mathbf{F} }_{q} $ of odd characteristic can be written as the sum of two irreducible monic elements in
${\mathbf{F} }_{q} $ of odd characteristic can be written as the sum of two irreducible monic elements in 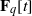 ${\mathbf{F} }_{q} [t] $ of degrees
${\mathbf{F} }_{q} [t] $ of degrees  $n$ and
$n$ and 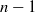 $n- 1$ if
$n- 1$ if 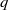 $q$ is larger than a bound depending only on
$q$ is larger than a bound depending only on  $n$. The main tool is a sufficient condition for simultaneous primality of two polynomials in one variable
$n$. The main tool is a sufficient condition for simultaneous primality of two polynomials in one variable  $x$ with coefficients in
$x$ with coefficients in 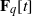 ${\mathbf{F} }_{q} [t] $.
${\mathbf{F} }_{q} [t] $.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2013
References
- 1
- Cited by


