Article contents
On the periods of Abelian functions in two variables
Published online by Cambridge University Press: 26 February 2010
Extract
Let Λ be a lattice in Cn such that the field 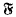 of Abelian functions on the quotient space Cn/Λ is of transcendence degree n. This implies that
of Abelian functions on the quotient space Cn/Λ is of transcendence degree n. This implies that 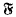 is an algebraic extension of a field
is an algebraic extension of a field 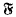 o of pure transcendence degree n. Thus there exists a vector A = (A1 …, An) of algebraically independent functions of the variable z = (z1, …, zn) and a function B = B(z), algebraic over
o of pure transcendence degree n. Thus there exists a vector A = (A1 …, An) of algebraically independent functions of the variable z = (z1, …, zn) and a function B = B(z), algebraic over
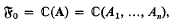
such that
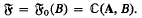
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1975
References
- 5
- Cited by


