Hostname: page-component-68945f75b7-qvshk Total loading time: 0 Render date: 2024-08-06T09:40:50.463Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE EXISTENCE OF SUPERGAUSSIAN DIRECTIONS ON CONVEX BODIES

Part of: General convexity

Published online by Cambridge University Press:  24 November 2011

Grigoris Paouris
Grigoris Paouris*
Affiliation:
Department of Mathematics, Texas A & M University, College Station, TX 77843, U.S.A. (email: grigoris@math.tamu.edu)
Get access

Abstract

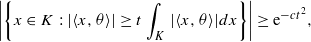We study the question of whether every centred convex body K of volume 1 in ℝn has “supergaussian directions”, which means θ∈Sn−1 such that for all 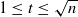, where c>0 is an absolute constant. We verify that a “random” direction is indeed supergaussian for isotropic convex bodies that satisfy the hyperplane conjecture. On the other hand, we show that if, for all isotropic convex bodies, a random direction is supergaussian then the hyperplane conjecture follows.

MSC classification

Secondary: 52A23: Asymptotic theory of convex bodies
Type
Research Article
Information
Mathematika , Volume 58 , Issue 2 , July 2012 , pp. 389 - 408
Copyright
Copyright © University College London 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alonso, D., Bastero, J., Bernues, J. and Wolff, P., On the isotropy constant of projections of polytopes. J. Funct. Anal. 258 (2010), 1452–1465.CrossRefGoogle Scholar
[2]Anttila, M., Ball, K. and Perissinaki, I., The central limit theorem for convex bodies. Trans. Amer. Math. Soc. 355 (2003), 4723–4735.CrossRefGoogle Scholar
[3]Ball, K. M., Logarithmically concave functions and sections of convex sets in ℝn. Studia Math. 88 (1988), 69–84.CrossRefGoogle Scholar
[4]Ball, K. M., Normed spaces with a weak-Gordon–Lewis property. In Functional Analysis (Austin, TX, 1987/1989) (Lecture Notes in Mathematics 1470), Springer (Berlin, 1991), 36–47.CrossRefGoogle Scholar
[5]Berwald, L., Verallgemeinerung eines Mittelswertsatzes von J. Favard für positive konkave Funkionen. Acta Math. 79 (1947), 17–37.CrossRefGoogle Scholar
[6]Bobkov, S. G. and Koldobsky, A., On the central limit property of convex bodies. In Geometric Aspects of Functional Analysis (Lecture Notes in Mathematics 1807) (eds Milman, V. D. and Schechtman, G.), Springer (Berlin, 2003), 44–52.CrossRefGoogle Scholar
[7]Bobkov, S. G. and Nazarov, F. L., On convex bodies and log-concave probability measures with unconditional basis. In Geometric Aspects of Functional Analysis (Lecture Notes in Mathematics 1807) (eds Milman, V. D. and Schechtman, G.), Springer (Berlin, 2003), 53–69.CrossRefGoogle Scholar
[8]Bobkov, S. G. and Nazarov, F. L., Large deviations of typical linear functionals on a convex body with unconditional basis. In Stochastic Inequalities and Applications (Progress in Probability 56), Birkhauser (Basel, 2003), 3–13.CrossRefGoogle Scholar
[9]Bourgain, J., On high dimensional maximal functions associated to convex bodies. Amer. J. Math. 108 (1986), 1467–1476.CrossRefGoogle Scholar
[10]Bourgain, J., On the distribution of polynomials on high dimensional convex sets. In Geometric Aspects of Functional Analysis (Lecture Notes in Mathematics 1469) (eds Lindenstrauss, J. and Milman, V. D.), Springer (Berlin, 1991), 127–137.CrossRefGoogle Scholar
[11]Bourgain, J., On the isotropy constant problem for ψ 2-bodies. In Geometric Aspects of Functional Analysis (Lecture Notes in Mathematics 1807) (eds Milman, V. D. and Schechtman, G.), Springer (Berlin, 2003), 114–121.CrossRefGoogle Scholar
[12]Borell, C., Complements of Lyapunov’s inequality. Math. Ann. 205 (1973), 323–331.CrossRefGoogle Scholar
[13]Borell, C., Convex set functions in d-space. Period. Math. Hungar. 6 (1975), 111–136.CrossRefGoogle Scholar
[14]Brehm, U. and Voigt, J., Asymptotics of cross sections for convex bodies. Beiträge Algebra Geom. 41 (2000), 437–454.Google Scholar
[15]Campi, S. and Gronchi, P., The L p-Busemann–Petty centroid inequality. Adv. Math. 167 (2002), 128–141.CrossRefGoogle Scholar
[16]Dafnis, N., Giannopoulos, A. and Guédon, O., On the isotropic constant of random polytopes. Adv. Geom. 10 (2010), 311–321.CrossRefGoogle Scholar
[17]Dafnis, N. and Paouris, G., Small ball probability estimates, ψ 2-behavior and the hyperplane conjecture. J. Funct. Anal. 258 (2010), 1933–1964.CrossRefGoogle Scholar
[18]Eldan, R. and Klartag, B., Pointwise Estimates for Marginals of Convex Bodies. J. Funct. Anal. 254 (2008), 2275–2293.CrossRefGoogle Scholar
[19]Fleury, B., Between Paouris concentration inequality and variance conjecture. Ann. Inst. Henri Poincaré Probab. Stat. 46(2) (2010), 299–312.CrossRefGoogle Scholar
[20]Fleury, B., Concentration in a thin Euclidean shell for log-concave measures. J. Funct. Anal. 259(4) (2010), 832–841.CrossRefGoogle Scholar
[21]Fleury, B., Guédon, O. and Paouris, G., A stability result for mean width of L p-centroid bodies. Adv. Math. 214 (2007), 865–877.CrossRefGoogle Scholar
[22]Giannopoulos, A., Notes on isotropic convex bodies. Warsaw University Notes, (2003). Available online in http://users.uoa.gr/∼apyiannop.Google Scholar
[23]Giannopoulos, A., Pajor, A. and Paouris, G., A note on subgaussian estimates for linear functionals on convex bodies. Proc. Amer. Math. Soc. 135 (2007), 2599–2606.CrossRefGoogle Scholar
[24]Giannopoulos, A., Paouris, G. and Valettas, P., On the existence of subgaussian directions for log-concave measures. In Proc. Workshop on Concentration, Functional Inequalities and Isoperimetry (Contemporary Mathematics 545), American Mathematical Society (Providence, RI, 2011), 109–148.Google Scholar
[25]Guédon, O. and Milman, E., Interpolating thin-shell and sharp large-deviation estimates for isotropic log-concave measures. Preprint, arXiv:1011.0943.Google Scholar
[26]Hensley, D., Slicing convex bodies, bounds of slice area in terms of the body’s covariance. Proc. Amer. Math. Soc. 79 (1980), 619–625.Google Scholar
[27]Junge, M., On the hyperplane conjecture for quotient spaces of L p. Forum Math. 6 (1994), 617–635.CrossRefGoogle Scholar
[28]Kannan, R., Lovász, L. and Simonovits, M., Isoperimetric problems for convex bodies and a localization lemma. Discrete Comput. Geom. 13 (1995), 541–559.CrossRefGoogle Scholar
[29]Klartag, B., On convex perturbations with a bounded isotropic constant. Geom. Funct. Anal. 16 (2006), 1274–1290.CrossRefGoogle Scholar
[30]Klartag, B., A central limit theorem for convex sets. Invent. Math. 168 (2007), 91–131.CrossRefGoogle Scholar
[31]Klartag, B., Power-law estimates for the central limit theorem for convex sets. J. Funct. Anal. 245 (2007), 284–310.CrossRefGoogle Scholar
[32]Klartag, B., Uniform almost sub-gaussian estimates for linear functionals on convex sets. Algebra i Analiz (St. Petersburg Math. J.) 19(1) (2007), 109–148.Google Scholar
[33]Klartag, B., A Berry-Esseen type inequality for convex bodies with an unconditional basis. Probab. Theory Related Fields 45 (2009), 1–33.CrossRefGoogle Scholar
[34]Klartag, B., On nearly radial marginals of high-dimensional probability measures. J. Eur. Math. Soc. (JEMS) 12 (2010), 723–754.CrossRefGoogle Scholar
[35]Klartag, B. and Kozma, G., On the hyperplane conjecture for random convex sets. Israel J. Math. 170 (2009), 253–268.CrossRefGoogle Scholar
[36]Klartag, B. and Milman, E., Centroid bodies and the logarithmic Laplace transform—a unified approach. Preprint, arXiv:1103.2985v1.Google Scholar
[37]Klartag, B. and Vershynin, R., Small ball probability and Dvoretzky Theorem. Israel J. Math. 157 (2007), 193–207.CrossRefGoogle Scholar
[38]Koldobsky, A., Pajor, A. and Yaskin, V., Inequalities of the Kahane–Khinchin type and sections of L p-balls. Studia Math. 184(3) (2008), 217–231.CrossRefGoogle Scholar
[39]König, H., Meyer, M. and Pajor, A., The isotropy constants of the Schatten classes are bounded. Math. Ann. 312 (1998), 773–783.Google Scholar
[40]Latala, R. and Oleszkiewicz, K., Small ball probability estimates in terms of width. Studia Math. 169 (2005), 305–314.CrossRefGoogle Scholar
[41]Latala, R. and Wojtaszczyk, J. O., On the infimum convolution inequality. Studia Math. 189 (2008), 147–187.CrossRefGoogle Scholar
[42]Litvak, A., Milman, V. D. and Schechtman, G., Averages of norms and quasi-norms. Math. Ann. 312 (1998), 95–124.CrossRefGoogle Scholar
[43]Lutwak, E., Yang, D. and Zhang, G., L p affine isoperimetric inequalities. J. Differential Geom. 56 (2000), 111–132.CrossRefGoogle Scholar
[44]Lutwak, E. and Zhang, G., Blaschke–Santaló inequalities. J. Differential Geom. 47 (1997), 1–16.CrossRefGoogle Scholar
[45]Milman, E., On the role of convexity in isoperimetry, spectral gap and concentration. Invent. Math. 177 (2009), 1–43.CrossRefGoogle Scholar
[46]Milman, V. D., A new proof of A. Dvoretzky’s theorem in cross-sections of convex bodies. Funktsional. Anal. i Prilozen. 5 (1971), 28–37 (in Russian).Google Scholar
[47]Milman, V. D. and Pajor, A., Isotropic positions and inertia ellipsoids and zonoids of the unit ball of a normed n-dimensional space. In GAFA Seminar 87–89 (Lecture Notes in Mathematics 1376) , Springer (1989), 64–104.Google Scholar
[48]Milman, V. D. and Schechtman, G., Asymptotic Theory of Finite Dimensional Normed Spaces (Lecture Notes in Mathematics 1200), Springer (Berlin, 1986).Google Scholar
[49]Milman, V. D. and Schechtman, G., Global versus Local asymptotic theories of finite-dimensional normed spaces. Duke Math. J. 90 (1997), 73–93.CrossRefGoogle Scholar
[50]Paouris, G., Ψ2-estimates for linear functionals on zonoids. In Geometric Aspects of Functional Analysis (Lecture Notes in Mathematics 1807) (eds Milman, V. D. and Schechtman, G.), Springer (Berlin, 2003), 211–222.CrossRefGoogle Scholar
[51]Paouris, G., Concentration of mass on convex bodies. Geom. Funct. Anal. 16 (2006), 1021–1049.CrossRefGoogle Scholar
[52]Paouris, G., Small ball probability estimates for log-concave measures. Trans. Amer. Math. Soc. (2011), doi:10.1090/S0002-9947-2011-05411-5.CrossRefGoogle Scholar
[53]Pisier, G., The Volume of Convex Bodies and Banach Space Geometry (Cambridge Tracts in Mathematics 94), Cambridge University Press (Cambridge, 1989).CrossRefGoogle Scholar
[54]Pivovarov, P., On the volume of caps and bounding the mean-width of an isotropic convex body. Math. Proc. Cambridge Philos. Soc. 149(2) (2010), 317–331.CrossRefGoogle Scholar
[55]Schneider, R., Convex Bodies: the Brunn–Minkowski Theory (Encyclopedia of Mathematics and its Applications 44), Cambridge University Press (Cambridge, 1993).Google Scholar
[56]Sodin, S., An isoperimetric inequality on the ℓ np balls. Ann. Inst. Henri Poincaré Probab. Stat. 44 (2008), 362–373.CrossRefGoogle Scholar