Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-25T14:35:40.924Z Has data issue: false hasContentIssue false
  • English
  • Français

A MEAN VALUE RESULT FOR A PRODUCT OF GL(2) AND GL(3) 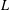$L$-FUNCTIONS

Part of: Asymptotic theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  17 April 2019

Olga Balkanova ,
Gautami Bhowmik ,
Dmitry Frolenkov  and
Nicole Raulf
Olga Balkanova
Affiliation:
Department of Mathematics and Statistics, University of Turku, Turku 20014, Finland Department of Mathematical Sciences, Chalmers University of Technology and University of Gothenburg, Chalmers tvärgata 3, 412 96 Gothenburg, Sweden email olgabalkanova@gmail.com
Gautami Bhowmik
Affiliation:
Laboratoire Painlevé LABEX-CEMPI, Université Lille, 59655 Villeneuve d’Ascq Cedex, France email bhowmik@math.univ-lille1.fr
Dmitry Frolenkov
Affiliation:
National Research University Higher School of Economics, Moscow, Russia Steklov Mathematical Institute of Russian Academy of Sciences, 8 Gubkina st., Moscow 119991, Russia email frolenkov@mi.ras.ru
Nicole Raulf
Affiliation:
Laboratoire Painlevé LABEX-CEMPI, Université Lille, 59655 Villeneuve d’Ascq Cedex, France email nicole.raulf@math.univ-lille1.fr
Get access

Abstract

In this paper various analytic techniques are combined in order to study the average of a product of a Hecke $L$-function and a symmetric square 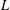$L$-function at the central point in the weight aspect. The evaluation of the second main term relies on the theory of Maaß forms of half-integral weight and the Rankin–Selberg method. The error terms are bounded using the Liouville–Green approximation.

MSC classification

Primary: 11F12: Automorphic forms, one variable
Secondary: 33C05: Classical hypergeometric functions, $_2F_1$ 34E05: Asymptotic expansions 34E20: Singular perturbations, turning point theory, WKB methods
Type
Research Article
Information
Mathematika , Volume 65 , Issue 3 , 2019 , pp. 743 - 762
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of Olga Balkanova is supported by Academy of Finland project no. 293876. Gautami Bhowmik acknowledges support from the Labex CEMPI. The research of Dmitry Frolenkov is supported by the Foundation for the Advancement of Theoretical Physics and Mathematics BASIS. Nicole Raulf acknowledges support from the Labex CEMPI.

References

Balkanova, O. and Frolenkov, D., Moments of L-functions and Liouville–Green method. J. Eur. Math. Soc. (JEMS) , to appear. Preprint, 2016, arXiv:1610.03465 [math.NT].Google Scholar
Balkanova, O. and Frolenkov, D., The mean value of symmetric square L-functions. Algebra Number Theory 12(1) 2018, 35–59.Google Scholar
Bykovskii, V. A., Density theorems and the mean value of arithmetic functions on short intervals. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 212 (1994), Anal. Teor. Chisel i Teor. Funktsii. 12, 56–70, 196 (in Russian); Engl. transl. J. Math. Sci. (New York) 83(6) (1997), 720–730.Google Scholar
Cohen, H., Sums involving the values at negative integers of L-functions of quadratic characters. Math. Ann. 217 1975, 271–285.Google Scholar
Conrey, B., Farmer, D. W., Keating, J. P., Rubinstein, M. O. and Snaith, N. C., Integral moments of L-functions. Proc. Lond. Math. Soc. 91 2005, 33–104.Google Scholar
Conrey, J. B. and Iwaniec, H., The cubic moment of central values of automorphic L-functions. Ann. of Math. (2) 151 2000, 1175–1216.Google Scholar
Diaconu, A., Goldfeld, D. and Hoffstein, J., Multiple Dirichlet series and moments of zeta and L-functions. Compos. Math. 139 2003, 297–360.Google Scholar
Goldfeld, D. and Hoffstein, J., Eisenstein series of 1/2-integral weight and the mean value of real Dirichlet L-series. Invent. Math. 80 1985, 185–208.Google Scholar
Iwaniec, H. and Michel, P., The second moment of the symmetric square L-functions. Ann. Acad. Sci. Fenn. Math. 26 2001, 465–482.Google Scholar
Iwaniec, H. and Sarnak, P., The non-vanishing of central values of automorphic L-functions and Landau–Siegel zeros. Israel J. Math. 120 2000, 155–177.Google Scholar
Khan, R., Non-vanishing of the symmetric square L-function at the central point. Proc. Lond. Math. Soc. 100(3) 2010, 736–762.Google Scholar
Kohnen, W., Modular forms of half integral weight on 𝛤0(4). Math. Ann. 248 1980, 249–266.Google Scholar
Lau, Y.-K., Royer, E. and Wu, J., Twisted moments of automorphic L-functions. J. Number Theory 130 2010, 2773–2802.Google Scholar
Maaß, H., Konstruktion ganzer Modulformen halbzahliger Dimension. Abh. Math. Semin. Univ. Hambg. 12 1937, 133–162.Google Scholar
Müller, W., The mean square of Dirichlet series associated with automorphic forms. Monatsh. Math. 113 1992, 121–159.Google Scholar
Munshi, R. and Sengupta, J., A case of simultaneous non-vanishing of automorphic L-functions. Acta Arith. 182(1) 2018, 1–11.Google Scholar
Ng, M.-H., Moments of automorphic $L$ -functions. PhD Thesis, University of Hong Kong, 2016.Google Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. and Clarke, C. W., NIST Handbook of Mathematical Functions, Cambridge University Press (Cambridge, 2010).Google Scholar
Petridis, Y., Raulf, N. and Risager, M., Double Dirichlet series and quantum unique ergodicity of weight one-half Eisenstein series. Algebra Number Theory 8(7) 2014, 1539–1595.Google Scholar
Pitale, A., Jacobi Maass forms. Abh. Math. Semin. Univ. Hambg. 79 2009, 87–111.Google Scholar
Royer, E. and Wu, J., Special values of symmetric power L-functions and Hecke eigenvalues. J. Théor. Nombres Bordeaux 19(3) 2007, 703–753.Google Scholar
Shimura, G., On modular forms of half integral weight. Ann. of Math. (2) 97(3) 1973, 440–481.Google Scholar
Shintani, T., On zeta-functions associated with the vector space of quadratic forms. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 22 1975, 25–65.Google Scholar
Zagier, D., Modular forms whose Fourier coefficients involve zeta-functions of quadratic fields. In Modular Functions of One Variable, VI (Proc. Second Internat. Conf., Univ. Bonn, Bonn, 1976) (Lecture Notes in Mathematics 627 ), Springer (Berlin, 1977), 105–169.Google Scholar