Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-23T10:09:05.033Z Has data issue: false hasContentIssue false
  • English
  • Français

Long mollifiers of the Riemann Zeta-function

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  26 February 2010

David W. Farmer
David W. Farmer
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027. U.S.A.
Get access

Extract

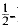The best current bounds for the proportion of zeros of ζ(s) on the critical line are due to Conrey [C], using Levinson's method [Lev]. This method can also be used to detect simple zeros on the critical line. To apply Levinson's method one first needs an asymptotic formula for the meansquare from 0 to T of ζ(s)M(s) near the -line, where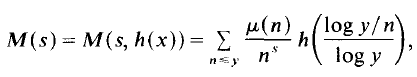

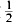where μ(n) is the Möbius function, h(x) is a real polynomial with h(0) = 0, and y=Tθ for some θ > 0. It turns out that the parameter θ is critical to the method: having an asymptotic formula valid for large values of θ is necessary in order to obtain good results. For example, if we let κ denote the proportion of nontrivial zeros of ζ(s) which are simple and on the critical line, then having the formula valid for 0 < θ < yields κ > 0·3562, having 0 < θ < 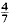gives κ > 0·40219, and it is necessary to have θ > 0·165 in order to obtain a positive lower bound for κ. At present, it is known that the asymptotic formula remains valid for 0 < θ < 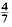, this is due to Conrey. Without assuming the Riemann Hypothesis, Levinson's method provides the only known way of obtaining a positive lower bound for κ.

MSC classification

Secondary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Type
Research Article
Information
Mathematika , Volume 40 , Issue 1 , June 1993 , pp. 71 - 87
Copyright
Copyright © University College London 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BCH-B.Balasubramanian, R., Conrey, J. B., and Heath-Brown, D. R.. Asymptotic mean square of the product of the Riemann zeta-function and a Dirichlet polynomial. J. reine angew. Math., 357 (1985), 161–181.Google Scholar
C.Conrey, J. B.. More than two fifths of the zeros of the Riemann zeta function are on the critical line. j reine angew. Math., 399 (1989), 1–26.Google Scholar
CG.Conrey, J. B. and Ghosh, A.. Mean Values of the Riemann zeta-function, III. Preprint.Google Scholar
CGG1.Conrey, J. B., Ghosh, A., and Gonek, S. M.. Mean values of the Riemann zeta-function with application to distribution of zeros. Number Theory, Trace Formulas and Discrete Groups, (1989), 185–199.Google Scholar
CGG2.Conrey, J. B., Ghosh, A., and Gonek, S. M.. Simple zeros of the Riemann zeta-function. To appear in J. Number Theory.Google Scholar
GG.Goldston, D. and Gonek, S. M.. Mean values of ζ1/ ζ (s) and primes in short intervals. Preprint.Google Scholar
G.Gonek, S. M.. On negative moments of the Riemann zeta-function. Mathematika, 36 (1989), 71–88.CrossRefGoogle Scholar
Lev.Levinson, N.. More than one-third of the zeros of Riemann's zeta-function are on (. Adv. in Math., 13 (1974), 383–436.CrossRefGoogle Scholar
Ml.Montgomery, H. L.. The pair correlation of zeros of the zeta function. Proc. Symp. Pure Math., 24 (1973), 181–193.CrossRefGoogle Scholar
M2.Montgomery, H. L.. Distribution of the zeros of the Riemann zeta function. Proc. of the Int. Cong, for Math., Vancouver, BC, 1 (1974), 379–381.Google Scholar
T.Titchmarsh, E. C.. The Theory of the Riemann Zeta-Function, 2nd Ed. (Oxford, 1986).Google Scholar