Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-27T01:12:15.664Z Has data issue: false hasContentIssue false
  • English
  • Français

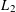$L_{2}$-SMALL DEVIATIONS FOR WEIGHTED STATIONARY PROCESSES

Part of: Integral, integro-differential, and pseudodifferential operators Stochastic processes

Published online by Cambridge University Press:  03 April 2018

Mikhail Lifshits  and
Alexander Nazarov
Mikhail Lifshits
Affiliation:
St. Petersburg State University, St. Petersburg, Universitetskii pr. 28, Russia MAI, Linköping University, Sweden email mikhail@lifshits.org
Alexander Nazarov
Affiliation:
St. Petersburg Department of Steklov Institute of Mathematics and St. Petersburg State University, St. Petersburg 191023, Russia email al.il.nazarov@gmail.com
Get access

Abstract

We find logarithmic asymptotics of 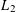$L_{2}$-small deviation probabilities for weighted stationary Gaussian processes (both for real and complex-valued) having a power-type discrete or continuous spectrum. Our results are based on the spectral theory of pseudo-differential operators developed by Birman and Solomyak.

MSC classification

Primary: 60G15: Gaussian processes
Secondary: 60G10: Stationary processes 60G22: Fractional processes, including fractional Brownian motion 47G30: Pseudodifferential operators
Type
Research Article
Information
Mathematika , Volume 64 , Issue 2 , 2018 , pp. 387 - 405
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ash, R. B. and Gardner, M. F., Topics in Stochastic Processes, Academic Press (New York, 1975).Google Scholar
Birman, M. Sh., Karadzhov, G. E. and Solomyak, M. Z., Boundedness conditions and spectrum estimates for the operators b (X)a (D) and their analogs. In Estimates and Asymptotics for Discrete Spectra of Integral and Differential Equations (Leningrad, 1989–90) (Advances in Soviet Mathematics 7 ), American Mathematical Society (Providence, RI, 1991), 85–106.Google Scholar
Birman, M. Š. and Solomjak, M. Z., Asymptotics of the spectrum of pseudodifferential operators with anisotropic-homogeneous symbols. Vestnik LGU(13) 1977, 13–21 (Russian). Engl. transl. Vestnik Leningrad Univ. Math. 10 (1982), 237–247.Google Scholar
Birman, M. Š. and Solomjak, M. Z., Asymptotics of the spectrum of pseudodifferential operators with anisotropic-homogeneous symbols. II. Vestnik LGU(3) 1979, 5–10 (Russian). Engl. transl. Vestnik Leningrad Univ. Math. 12 (1980), 155–161.Google Scholar
Birman, M. S. and Solomjak, M. Z., Spectral Theory of Self-Adjoint Operators in Hilbert Space, 2nd edn., revised and extended edn., Lan’ (St. Petersburg, 2010) (Russian). Engl. transl. of the 1st edn, Mathematics and Its Applications (Soviet Series 5), Kluwer, Dordrecht etc. 1987.Google Scholar
Bronski, J. C., Small ball constants and tight eigenvalue asymptotics for fractional Brownian motions. J. Theoret. Probab. 16(1) 2003, 87–100.Google Scholar
Dunker, T., Lifshits, M. A. and Linde, W., Small deviations of sums of independent variables. In Proc. Conf. High Dimensional Probability (Progress in Probability 43 ), Birkhäuser (Basel, 1998), 59–74.Google Scholar
Gao, F., Hannig, J., Lee, T.-Y. and Torcaso, F., Laplace transforms via Hadamard factorization with applications to small ball probabilities. Electronic J. Probab. 8 2003, paper 13, 1–20.Google Scholar
Gao, F., Hannig, J., Lee, T.-Y. and Torcaso, F., Exact L 2 -small balls of Gaussian processes. J. Theoret. Probab. 17(2) 2004, 503–520.Google Scholar
Gengembre, S., Probabilités de petites déviations pour les processus stationnaires gaussiens. Publ. IRMA Lille 60(X) 2003, 1–24.Google Scholar
Gengembre, S., Petites déviations pour les processus fractionnaires. Memoire de D.E.A. Université Lille I, 2002, 19 pp.Google Scholar
Hong, S. Y., Lifshits, M. and Nazarov, A., Small deviations in L 2 -norm for Gaussian dependent sequences. Electronic Comm. Probab. 21(41) 2016, 1–9.Google Scholar
Kaarakka, T. and Salminen, P., On fractional Ornstein–Uhlenbeck processes. Comm. Stoch. Anal. 5(1) 2011, 121–133.Google Scholar
Li, W. V. and Shao, Q.-M., Gaussian processes: inequalities, small ball probabilities and applications. In Stochastic Processes: Theory and Methods, Handbook of Statistics, Vol. 19 (eds Rao, C. R. and Shanbhag, D.), North-Holland/Elsevier (Amsterdam, 2001), 533–597.Google Scholar
Lifshits, M. A., Asymptotic behavior of small ball probabilities. In Probab. Theory and Math. Statist. Proc. VII International Vilnius Conference (1998) (ed. Grigelionis, B.), VSP/TEV (Vilnius/Utrecht, 1999), 453–468.Google Scholar
Lifshits, M. A., “Small deviations for stochastic processes and related topics” website. Bibliography of small deviation probabilities, http://www.proba.jussieu.fr/pageperso/smalldev/biblio.pdf.Google Scholar
Lifshits, M. A. and Linde, W., Small deviations of weighted fractional processes and average non-linear approximation. Trans. Amer. Math. Soc. 357 2005, 2059–2079.Google Scholar
Nazarov, A. I., Log-level comparison principle for small ball probabilities. Statist. Probab. Lett. 79(4) 2009, 481–486.Google Scholar
Nazarov, A. I., Exact L 2 -small ball asymptotics of Gaussian processes and the spectrum of boundary-value problems. J. Theor. Probab. 22(3) 2009, 640–665.Google Scholar
Nazarov, A. I. and Nikitin, Ya. Yu., Logarithmic L 2 -small ball asymptotics for some fractional Gaussian processes. Theory Probab. Appl. 49(4) 2004, 645–658.CrossRefGoogle Scholar
Nazarov, A. I. and Pusev, R. S., Comparison theorems for the small ball probabilities of Gaussian processes in weighted L 2 -norms. Algebra & Analysis 25(3) 2013, 131–146 (Russian). Engl. transl. St. Petersburg Math. J. 25(3) (2014), 455–466.Google Scholar
Neeser, F. and Massey, J., Proper complex random processes with applications to information theory. IEEE Trans. Inform. Theory 39(4) 1993, 1293–1302.Google Scholar
Ollila, E., On the circularity of a complex random variable. IEEE Signal Process. Lett. 15 2008, 841–844.Google Scholar
Pusev, R. S., Asymptotics of small deviations of the Bogoliubov processes with respect to a quadratic norm. Theoret. Math. Phys. 165(1) 2010, 1348–1357.CrossRefGoogle Scholar
Sankovich, D. P., Some properties of functional integrals with respect to the Bogoliubov measure. Theoret. Math. Phys. 126(1) 2001, 121–135.Google Scholar
Zolotarev, V. M., Asymptotic behavior of Gaussian measure in ℓ 2 . J. Sov. Math. 35 1986, 2330–2334.Google Scholar
Zygmund, A., Trigonometrical Series, Vol. 1, Cambridge University Press (Cambridge, 1959).Google Scholar