Article contents
HILBERT TRANSFORMS ALONG LIPSCHITZ DIRECTION FIELDS: A LACUNARY MODEL
Published online by Cambridge University Press: 09 February 2017
Abstract
We prove bounds for the truncated directional Hilbert transform in 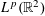 $L^{p}(\mathbb{R}^{2})$ for any
$L^{p}(\mathbb{R}^{2})$ for any 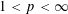 $1<p<\infty$ under a combination of a Lipschitz assumption and a lacunarity assumption. It is known that a lacunarity assumption alone is not sufficient to yield boundedness for
$1<p<\infty$ under a combination of a Lipschitz assumption and a lacunarity assumption. It is known that a lacunarity assumption alone is not sufficient to yield boundedness for 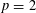 $p=2$, and it is a major question in the field whether a Lipschitz assumption alone suffices, at least for some
$p=2$, and it is a major question in the field whether a Lipschitz assumption alone suffices, at least for some 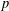 $p$.
$p$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2017
References
- 4
- Cited by


