Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T18:43:01.562Z Has data issue: false hasContentIssue false
  • English
  • Français

HAUSDORFF DIMENSIONS OF SOME LIMINF SETS IN DIOPHANTINE APPROXIMATION

Part of: Diophantine approximation, transcendental number theory Classical measure theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  17 September 2014

Bao-Wei Wang ,
Zhi-Ying Wen  and
Jun Wu
Bao-Wei Wang
Affiliation:
School of Mathematics and Statistics, Huazhong University of Science and Technology, 430074 Wuhan, China email bwei_wang@hust.edu.cn
Zhi-Ying Wen
Affiliation:
Department of Mathematical Sciences, Tsinghua University, 10084 Beijing, China email wenzy@tsinghua.edu.cn
Jun Wu
Affiliation:
School of Mathematics and Statistics, Huazhong University of Science and Technology, 430074 Wuhan, China email jun.wu@mail.hust.edu.cn
Get access

Abstract

Let 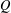$Q$ be an infinite subset of 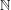$\mathbb{N}$. For any 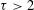${\it\tau}>2$, denote $W_{{\it\tau}}(Q)$ (respectively 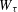$W_{{\it\tau}}$) to be the set of ${\it\tau}$ well-approximable points by rationals with denominators in $Q$ (respectively in 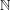$\mathbb{N}$). We consider the Hausdorff dimension of the liminf set 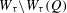$W_{{\it\tau}}\setminus W_{{\it\tau}}(Q)$ after Adiceam. By using the tools of continued fractions, it is shown that if 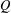$Q$ is a so-called 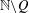$\mathbb{N}\setminus Q$-free set, the Hausdorff dimension of 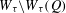$W_{{\it\tau}}\setminus W_{{\it\tau}}(Q)$ is the same as that of $W_{{\it\tau}}$, i.e. 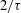$2/{\it\tau}$.

MSC classification

Primary: 11J83: Metric theory
Secondary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension 28A78: Hausdorff and packing measures
Type
Research Article
Information
Mathematika , Volume 61 , Issue 1 , January 2015 , pp. 101 - 120
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adiceam, F., A note on the Hausdorff dimension of some liminf sets appearing in simutaneous Diophantine approximation. Mathematika 59(1) 2013, 56–64.CrossRefGoogle Scholar
Adiceam, F., Liminf sets in simutaneous Diophantine approximation. Preprint, 2013,arXiv:1308.3806.Google Scholar
Besicovitch, A. S., Sets of fractional dimension (IV): on rational approximation to real numbers. J. Lond. Math. Soc. (2) 9 1934, 126–131.Google Scholar
Borosh, I. and Fraenkel, A. S., A generalization of Jarník’s theorem on Diophantine approximation. Nederl. Akad. Wet. Proc. Ser. A 75 1972, 193–201.Google Scholar
Bosma, W., Dajani, K. and Kraaikamp, C., Entropy quotients and correct digits in number-theoretic expansions. In Dynamics & Stochastics (Institute of Mathematical Statistics Lecture Notes Monograph Series 48), Institute of Mathematical Statistics (Beachwood, OH, 2006), 176–188.Google Scholar
Falconer, K. J., Fractal Geometry, Mathematical Foundations and Application, John Wiley & Sons (1990).Google Scholar
Hanus, P., Mauldin, D. and Urbański, M., Thermodynamic formalism and multifractal analysis of conformal infinite iterated function systems. Acta Math. Hungar. 96(1–2) 2002, 27–98.CrossRefGoogle Scholar
Harman, G., Metric Number Theory (London Mathematical Society Monographs New Series 18), Clarendon Press (Oxford, 1998).CrossRefGoogle Scholar
Hinokuma, T. and Shiga, H., Hausdorff dimension of sets arising in Diophantine approximation. Kodai Math. J. 19 1996, 365–377.Google Scholar
Iosifescu, M. and Kraaikamp, C., Metrical Theory of Continued Fractions (Mathematics and Its Applications 547), Kluwer Academic Publishers (Dordrecht, 2002).CrossRefGoogle Scholar
Jarník, V., Über die simultanen diophantischen Approximationen. Math. Z. 33 1931, 505–543.Google Scholar
Ya. Khintchine, A., Continued Fractions, P. Noordhoff (Groningen, The Netherlands, 1963).Google Scholar
Mauldin, D. and Urbański, M., Dimensions and measures in infinite iterated function systems. Proc. Lond. Math. Soc. 73(3) 1996, 105–154.Google Scholar
Mauldin, D. and Urbański, M., Graph Directed Markov Systems. Geometry and Dynamics of Limit Sets (Cambridge Tracts in Mathematics 148), Cambridge University Press (Cambridge, 2003).CrossRefGoogle Scholar
Wang, B.-W. and Wu, J., Hausdorff dimension of certain sets in continued fractions. Adv. Math. 218 2008, 1319–1339.CrossRefGoogle Scholar
Wu, J., Continued fraction and decimal expansions of an irrational number. Adv. Math. 206(2) 2006, 684–694.CrossRefGoogle Scholar