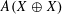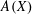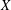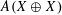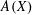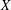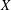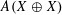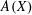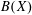Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
LEIDERMAN, ARKADY
and
MORRIS, SIDNEY A.
2020.
EMBEDDINGS OF FREE TOPOLOGICAL VECTOR SPACES.
Bulletin of the Australian Mathematical Society,
Vol. 101,
Issue. 2,
p.
311.
Leiderman, Arkady G.
and
Tkachenko, Mikhail G.
2024.
Embedding the free topological group $$F(X^n)$$ into F(X).
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 118,
Issue. 3,