Article contents
Cubic Diophantine inequalities
Published online by Cambridge University Press: 26 February 2010
Extract
It was shown by Davenport and Roth [7] that the values taken by
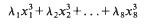
at integer points ( x1, …, x8) ∈ ℤ8 are dense on the real line, providing at least one of the ratios λi/λj, is irrational. Here and throughout, λi denote such nonzero real numbers. More precisely, Liu, Ng and Tsang [8] showed that for all  the inequality
the inequality

has infinitely many solutions in integers. Later Baker [1] obtained the same result in the enlarged range  . In this note we improve this further, the progress being considerable.
. In this note we improve this further, the progress being considerable.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1988
References
- 5
- Cited by


