Article contents
A COUNTEREXAMPLE TO A CONJECTURE OF LARMAN AND ROGERS ON SETS AVOIDING DISTANCE 1
Published online by Cambridge University Press: 14 May 2019
Abstract
For each 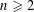 $n\geqslant 2$ we construct a measurable subset of the unit ball in
$n\geqslant 2$ we construct a measurable subset of the unit ball in 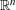 $\mathbb{R}^{n}$ that does not contain pairs of points at distance 1 and whose volume is greater than
$\mathbb{R}^{n}$ that does not contain pairs of points at distance 1 and whose volume is greater than 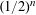 $(1/2)^{n}$ times the volume of the unit ball. This disproves a conjecture of Larman and Rogers from 1972.
$(1/2)^{n}$ times the volume of the unit ball. This disproves a conjecture of Larman and Rogers from 1972.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2019
Footnotes
The second author was partially supported by the SFB/TRR 191 “Symplectic Structures in Geometry, Algebra and Dynamics”, funded by the DFG, and the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie agreement number 764759.
References
- 2
- Cited by


