Article contents
CENTRAL LIMIT THEOREM FOR PLANCK-SCALE MASS DISTRIBUTION OF TORAL LAPLACE EIGENFUNCTIONS
Published online by Cambridge University Press: 12 April 2019
Abstract
We study the fine-scale 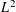 $L^{2}$-mass distribution of toral Laplace eigenfunctions with respect to random position in two and three dimensions. In two dimensions, under certain flatness assumptions on the Fourier coefficients and generic restrictions on energy levels, both the asymptotic shape of the variance is determined and the limiting Gaussian law is established in the optimal Planck-scale regime. In three dimensions the asymptotic behaviour of the variance is analysed in a more restrictive scenario (“Bourgain’s eigenfunctions”). Other than the said precise results, lower and upper bounds are proved for the variance under more general flatness assumptions on the Fourier coefficients.
$L^{2}$-mass distribution of toral Laplace eigenfunctions with respect to random position in two and three dimensions. In two dimensions, under certain flatness assumptions on the Fourier coefficients and generic restrictions on energy levels, both the asymptotic shape of the variance is determined and the limiting Gaussian law is established in the optimal Planck-scale regime. In three dimensions the asymptotic behaviour of the variance is analysed in a more restrictive scenario (“Bourgain’s eigenfunctions”). Other than the said precise results, lower and upper bounds are proved for the variance under more general flatness assumptions on the Fourier coefficients.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2019
Footnotes
Current address: Department of Mathematics, University of Haifa, 3498838 Haifa, Israel email nyesha@univ.haifa.ac.il
References
- 6
- Cited by


