Article contents
All-sum sets in (0,1]—Category and measure
Published online by Cambridge University Press: 26 February 2010
Abstract
We provide a unified and simplified proof that for any partition of (0, 1] into sets that are measurable or have the property of Baire, one cell will contain an infinite sequence together with all of its sums (finite or infinite) without repetition. In fact any set which is large around 0 in the sense of measure or category will contain such a sequence. We show that sets with 0 as a density point have very rich structure. Call a sequence 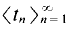 and its resulting all-sums set structured provided for each
and its resulting all-sums set structured provided for each 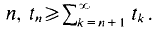 We show further that structured all-sums sets with positive measure are not partition regular even if one allows shifted all-sums sets. That is, we produce a two cell measurable partition of (0, 1 ] such that neither set contains a translate of any structured all-sums set with positive measure.
We show further that structured all-sums sets with positive measure are not partition regular even if one allows shifted all-sums sets. That is, we produce a two cell measurable partition of (0, 1 ] such that neither set contains a translate of any structured all-sums set with positive measure.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1997
References
- 3
- Cited by


