Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-25T08:28:04.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Additive Diophantine inequalities with mixed powers II

Published online by Cambridge University Press:  26 February 2010

Jörg Brüdern
Jörg Brüdern
Affiliation:
Geismar Landstrasse 97, 3400 Göttingen, West Germany.
Get access

Extract

A classical problem in the additive theory of numbers is the determination of the minimal s such that for all sufficiently large n the equation

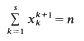
is solvable in natural numbers xk. Improving on earlier results the author [2] has been able to prove that one may take s = 18. In a survey article W. Schwarz asked for an analogue for diophantine inequalities [6]. As a first contribution to this subject we prove

Theorem. Let λ2, …, λ23 be nonzero real numbers, λ2/λ3 irrational. Then the values taken by

at integer points ( x1, …, x22) are dense on the real line.

Type
Research Article
Information
Mathematika , Volume 34 , Issue 2 , December 1987 , pp. 131 - 140
Copyright
Copyright © University College London 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baker, R. C. and Harman, G.. Diophantine inequalities with mixed powers. J. Number Theory, 18 (1984), 69–85.CrossRefGoogle Scholar
2.Brüdern, J.. Sums of squares and higher power II. J. Lond. Math. Soc. (2), 35 (1987), 244–250.CrossRefGoogle Scholar
3.Brüdern, J.. Additive diophantine inequalities with mixed powers I. Mathematika, 34 (1987), 124–130.CrossRefGoogle Scholar
4.Davenport, H.. Indefinite quadratic forms in many variables. Mathematika, 3 (1956), 81–101.CrossRefGoogle Scholar
5.Davenport, H. and Heilbronn, H.. On indefinite quadratic forms in five variables. J. Lond. Math. Soc., 21 (1946), 185–193.CrossRefGoogle Scholar
6.Schwarz, W.. Survey on analogues of the Waring problem: diophantine inequalities. In: Additive Number Theory (Seminaire theorie des nombres, Bordeaux, 1977).Google Scholar
7.Thanigasalam, K.. On sums of powers and a related problem. Acta Arith., 36 (1980), 125–141.CrossRefGoogle Scholar
8.Vaughan, R. C.. On sums of mixed powers. J. Lond. Math. Soc. (2). 3 (1971), 677–688.CrossRefGoogle Scholar
9.Vaughan, R. C.. Diophantine approximation by prime numbers II. Proc. Lond. Math Soc. (3), 28 (1974), 385–401.CrossRefGoogle Scholar
10.Vaughan, R. C.. The Hardy-Littlewood method (Cambridge, 1981).Google Scholar
11.Watson, G. L.. On idenfinite quadratic forms in five variables. Proc. Lond. Math. Soc. (3), 3 (1953), 170–181.CrossRefGoogle Scholar