Article contents
Lattice coverings of space
Published online by Cambridge University Press: 26 February 2010
Extract
Let K be a n-dimensional convex body. A lattice Λ will be called a covering lattice for K (or simply a covering lattice), if each point of space has at least one representation in the form k + g where k ε K and g ε Λ. The density ϑ(K, Λ) of the resultant covering of the whole of space by the bodies of the form K + g with g ε Λ is, quite naturally, defined to be the ratio V(K)/d(Λ), where V(K) is the volume of K and d(Λ) is the determinant of Λ (i.e. the volume of its fundamental parallepipeds). Clearly this density is at least 1. A number of authors, in particular H. Davenport [3], R. P. Bambah and K. F. Roth [2], G. L. Watson [8], C. A. Rogers [4], [5] and W. Schmidt [7], have either constructed or proved the existence of lattices for which the density ϑ(K, Λ) is reasonably small. But, when n is large, all the densities obtained are of the form cn where c is a constant greater than 1. The object of this note is to obtain some rather stronger results. In the general case we prove the existence of covering lattices Λ with
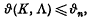
Where

as n→∞.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1959
References
- 36
- Cited by


