Article contents
A generalization of Ascoli's theorem
Published online by Cambridge University Press: 26 February 2010
Extract
In its simplest form, the theorem of Ascoli with which we are concerned is an extension of the Bolzano-Weierstrass theorem: it states that, if X and Y are bounded closed sets, of real or complex numbers, and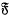 is a sequence of equicontinuous functions mapping X into Y, then
is a sequence of equicontinuous functions mapping X into Y, then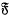 has a uniformly convergent subsequence. As is well known, this result has played a fundamental part in the development of several theories; it has also been widely generalized, by processes of abstraction and localization, and a very useful version of the theorem runs as follows (cf. [4], 233–234):
has a uniformly convergent subsequence. As is well known, this result has played a fundamental part in the development of several theories; it has also been widely generalized, by processes of abstraction and localization, and a very useful version of the theorem runs as follows (cf. [4], 233–234):
(A) Suppose that X is a locally compact regular space, and that Y is a Hausdorff space whose topology is determined by a uniform structure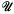 . Let YX be the space of all functions that map X into Y, with the topology of locally uniform convergence with respect to
. Let YX be the space of all functions that map X into Y, with the topology of locally uniform convergence with respect to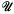 . Then a closed set
. Then a closed set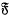 in YX is compact if, at each point x of X, (i) the set
in YX is compact if, at each point x of X, (i) the set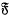 (x) is relatively compact, in Y, and, (ii)
(x) is relatively compact, in Y, and, (ii) 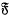 is equicontinuous with respect to
is equicontinuous with respect to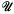 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1959
References
- 1
- Cited by


