Research Article
A formalization of an ℵ0-valued propositional calculus
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 367-376
-
- Article
- Export citation
Two theorems on Engel groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 377-380
-
- Article
- Export citation
The codifying of tree-structure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 381-385
-
- Article
- Export citation
Some results concerning the local analytic branches of an algebraic variety
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 386-396
-
- Article
- Export citation
Hyperelliptic threefolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 397-409
-
- Article
- Export citation
On the invariants of the canonical system of a Vd
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 410-412
-
- Article
- Export citation
A theorem of Minkowski on the product of two linear forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 413-420
-
- Article
- Export citation
Algebraic integers with two conjugates outside the unit circle
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-436
-
- Article
- Export citation
A correction to a paper on the dimension of Cartesian product sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 437-440
-
- Article
- Export citation
On the partial sums of series of hypergeometric type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 441-445
-
- Article
- Export citation
The roots of J−(l + ½) (λη)Jl + ½ (λ) − Jl + ½ (λη) J−(l + ½)(λ) = 0
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 446-448
-
- Article
- Export citation
On the distribution of queueing times
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 449-461
-
- Article
- Export citation
A Frequency-function form of the central limit theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 462-472
-
- Article
- Export citation
Stochastic processes associated with random divisions of a line
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 473-485
-
- Article
- Export citation
A case of gaseous accretion
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 486-492
-
- Article
- Export citation
A note on the unsteady motion of a compressible fluid
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 493-497
-
- Article
- Export citation
On the dynamical theory of the rotation of the earth. II. The effect of precession on the motion of the liquid core
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 498-515
-
- Article
- Export citation
On the oscillations of a bowed string
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 516-530
-
- Article
- Export citation
On the energy scattered from the interaction of turbulence with sound or shock waves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 531-551
-
- Article
- Export citation
On the decrease of velocity with depth in an irrotational water wave
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 552-560
-
- Article
- Export citation



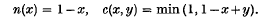
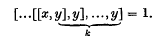

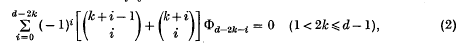
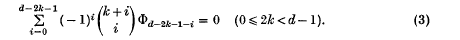

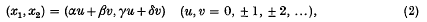
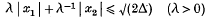
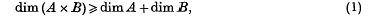
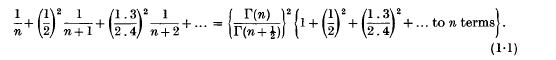
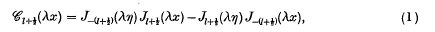
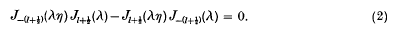
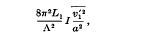
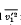 is the mean square velocity and
is the mean square velocity and 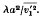 .
.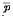 increase with
increase with