Research Article
On semigroup algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-15
-
- Article
- Export citation
Remarks on the isomorphism problem in theories of construction of finite groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 16-24
-
- Article
- Export citation
Finite groups having unique proper characteristic subgroups. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-36
-
- Article
- Export citation
Note on nilpotent and solvable algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-40
-
- Article
- Export citation
The solution of equations by iteration
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 41-43
-
- Article
- Export citation
Compact linear operators of volterra type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 44-55
-
- Article
- Export citation
On conformal mappings of domains of infinite connectivity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 56-64
-
- Article
- Export citation
On Ingham summability and summability by Lambert series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 65-80
-
- Article
- Export citation
On Kepler's equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 81-91
-
- Article
- Export citation
The central limit theorem for m-dependent variables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 92-95
-
- Article
- Export citation
A note on recurrent events
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 96-102
-
- Article
- Export citation
The bound state representation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-112
-
- Article
- Export citation
Temporally ordered graphs in quantum field theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 113-120
-
- Article
- Export citation
The retardation of alpha particles when capture and loss occur
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 121-125
-
- Article
- Export citation
Approximate wave functions, with exchange for Mn+2
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 126-130
-
- Article
- Export citation
Physical properties of particles obeying generalized statistics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 131-140
-
- Article
- Export citation
The ehrenfests' wind-wood model in two dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 141-148
-
- Article
- Export citation
The edge conditions and field representation theorems in the theory of electromagnetic diffraction
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 149-161
-
- Article
- Export citation
The character of the equilibrium of an incompressible heavy viscous fluid of variable density
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 162-178
-
- Article
- Export citation
The character of the equilibrium of an incompressible heavy viscous fluid of variable density: an approximate theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-201
-
- Article
- Export citation



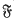 , the concept of the group algebra (group ring) over
, the concept of the group algebra (group ring) over 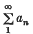 defined by
defined by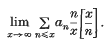

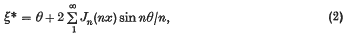
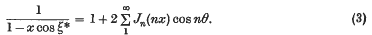
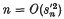 for large
for large 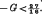 . Otherwise, the possibility of a disturbance being propagated as a horizontal wave does arise, but only within a limited wave-length range.
. Otherwise, the possibility of a disturbance being propagated as a horizontal wave does arise, but only within a limited wave-length range.