Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-23T20:28:31.764Z Has data issue: false hasContentIssue false
  • English
  • Français

The word problem for the bifree combinatorial strict regular semigroup

Published online by Cambridge University Press:  24 October 2008

Karl Auinger
Karl Auinger
Affiliation:
Institut für Mathematik, Strudlhofgasse 4, A-1090 Wien, Austria
Get access Rights & Permissions [Opens in a new window]

Abstract

A class of regular semigroups closed under taking direct products, regular subsemigroups and homomorphic images is an e(xistence) -variety of regular semigroups. The class 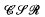of all combinatorial strict regular semigroups is the e-variety generated by the five element non-orthodox completely 0-simple semigroup and consists of all regular subdirect products of combinatorial completely 0-simple semigroups and/or rectangular bands. The bifree object 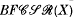on the set X in 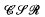is the natural concept of a ‘free object’ in the class 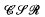. 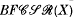is generated by the set X and the set of formal inverses X′ under the two binary operations of multiplication · and forming the sandwich element ∧A. Hence 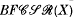is a homomorphic image of the absolutely free algebra 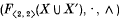of type 〈2, 2〉 generated by X ∪X′. In this paper we shall describe the associated congruence on F〈2, 2〉(X∪X′) and construct a model of 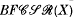in terms of sets and binary relations. As an application, a model of the free strict pseudosemilattice on a set X is obtained.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 113 , Issue 3 , May 1993 , pp. 519 - 533
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Auinger, K.. Free strict inverse semigroups. J. Algebra, to appear.Google Scholar
[2]Auinger, K.. Bifree objects in e-varieties of strict orthodox semigroups and the lattice of strict orthodox *-semigroup varieties. Glasgow Math. J., to appear.Google Scholar
[3]Auinger, K.. On the lattice of existence varieties of locally inverse semigroups. Preprint.Google Scholar
[4]Auinger, K.. The bifree locally inverse semigroup on a set. J. Algebra, to appear.Google Scholar
[5]Grätzer, G.. Universal Algebra (Van Nostrand, 1968).Google Scholar
[6]Hall, T. E.. Identities for existence varieties of regular semigroups. Bull. Austral. Math. Soc. 40 (1989), 59–77.CrossRefGoogle Scholar
[7]Hall, T. E.. Regular semigroups: amalgamation and the lattice of existence varieties. Algebra Universalis 29 (1991), 79–108.CrossRefGoogle Scholar
[8]Hall, T. E.. A concept of variety for regular semigroups. In Semigroup Theory, Proceedings of the Monash University Conference, on Semigroup Theory in Honor of G. P. Preston (Hall, T. E., Meakin, J. C. and Jones, P. R., eds.) (World Scientific, 1991), pp. 101–116.Google Scholar
[9]Harary, F.. Graph Theory (Addison-Wesley, 1971).Google Scholar
[10]Howie, J. M.. An Introduction to Semigroup Theory (Academic Press, 1976).Google Scholar
[11]Kaďourek, J. and Szendrei, M. B.. A new approach in the theory of orthodox semigroups. Semigroup Forum 40 (1990), 257–296.CrossRefGoogle Scholar
[12]Lallement, G.. Demi-groupes réguliers. Ann. Math. Pura Appl. 77 (1967), 47–130.CrossRefGoogle Scholar
[13]Margolis, S. W., Meakin, J. C. and Stephen, J. B.. Free objects in certain varieties of inverse semigroups. Canad. J.Math. 42 (1990), 1084–1097.CrossRefGoogle Scholar
[14]Meakin, J. C.. Local semilattices on two generators. Semigroup Forum 24 (1982), 95–116.CrossRefGoogle Scholar
[15]Meakin, J. C.. The free local semilattice on a set. J. Pure Appl. Algebra 27 (1983), 263–275.CrossRefGoogle Scholar
[16]Meakin, J. C. and Pastijn, F.. The structure of pseudosemilattices. Algebra Universalis 13 (1981), 355–372.CrossRefGoogle Scholar
[17]Meakin, J. C. and Pastijn, F.. The free pseudosemilattice on two generators. Algebra Universalis 14 (1982), 297–309.CrossRefGoogle Scholar
[18]Nambooripad, K. S. S.. Structure of Regular Semigroups. Memoirs 224 (American Mathematical Society, 1979).CrossRefGoogle Scholar
[19]Nambooripad, K. S. S.. The natural partial order on a regular semigroup. Proc. Edinburgh Math. Soc. (2) 23 (1980), 249–260.CrossRefGoogle Scholar
[20]Nambooripad, K. S. S.. Pseudosemilattices and biordered sets I. Simon Stevin 55 (1981), 103–110.Google Scholar
[21]Nambooripad, K. S. S.. Pseudosemilattices and biordered sets II. Simon Stevin 56 (1982), 143–160.Google Scholar
[22]Nambooripad, K. S. S.. Pseudosemilattices and biordered sets III. Simon Stevin 56 (1982), 239–256.Google Scholar
[23]Pastijn, F.. Rectangular bands of inverse semigroups. Simon Stevin 56 (1982), 1–97.Google Scholar
[24]Pastijn, F.. The structure of pseudo-inverse semigroups. Trans. Amer. Math. Soc. 273 (1982), 631–655.CrossRefGoogle Scholar
[25]Pastijn, F.. Regular locally testable semigroups as semigroups of quasi-ideals. Ada Math. Acad. Sci. Hungar. 36 (1980), 161–166.CrossRefGoogle Scholar
[26]Petrich, M.. Regular semigroups satisfying certain conditions on idempotents and ideals. Trans. Amer. Math. Soc. 170 (1972), 245–267.CrossRefGoogle Scholar
[27]Petrich, M.. Completely semisimple semigroups whose idempotents form a tree. J. Reine Angew. Math. 283/284 (1972), 125–146.Google Scholar
[28]Petrich, M.. Inverse Semigroups (Wiley, 1984).Google Scholar
[29]Reilly, N. R.. Free combinatorial strict inverse semigroups, J. London Math. Soc. (2) 39 (1989), 102–120.CrossRefGoogle Scholar
[30]Schein, B. M.. Pseudosemilattices and pseudolattices. Amer. Math. Soc. Transl. 119 (1983), 1–16.Google Scholar
[31]Shevrin, L. N. and Volkov, M. V.. Identities in semigroups (Russian). Izv. Vyssh. Uchebn. Zaved. Mat. 11 (1985), 3–47.Google Scholar
[32]Szendrei, M. B.. Free *-orthodox semigroups. Simon Stevin 59 (1985), 175–201.Google Scholar
[33]Trahtman, A. N.. Varieties of n-testable semigroups. Semigroup Forum 27 (1983), 309–318.CrossRefGoogle Scholar
[34]Trotter, P. G.. Normal partitions of idempotents of regular semigroups. J. Austral. Math. Soc. Ser. A 26 (1978), 110–114.CrossRefGoogle Scholar
[35]Yeh, Y. T.. The existence of e-free objects in e-varieties of regular semigroups. Internat. J. Algebra Comput., to appear.Google Scholar
[36]Yeh, Y. T.. On existence varieties of E-solid or locally inverse semigroups and e-invariant congruences. J. Algebra, to appear.Google Scholar
[37]Zalcstein, Y.. Locally testable semigroups. Semigroup Forum 5 (1973), 216–227.CrossRefGoogle Scholar