Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T15:51:53.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Twisting formulae of the Jones polynomial

Published online by Cambridge University Press:  24 October 2008

Yoshiyuki Yokota
Yoshiyuki Yokota
Affiliation:
Department of Mathematics, School of Science and Engineering, Waseda University, Ohkubo, Shinjuku, Tokyo, 169, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

Let 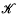be an oriented knot in S3 and 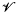a solid torus endowed with a preferred framing which contains 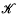in its interior. By ρ and λ we denote the wrapping and winding numbers of 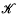in 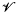respectively. That is, they are the geometric and algebraic intersection numbers of 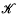and a meridian disk of 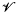. For an integer μ, let τμ be an orientation-preserving homeomorphism of 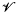satisfying τμ(m) = m and τμ(l) = l + μm in H1(∂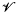), where (m, l) is a meridian-longitude pair of 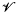. We call τμ(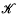), denoted by 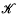μ, the knot obtained from 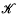by μ-twisting along .

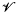Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 110 , Issue 3 , November 1991 , pp. 473 - 482
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Hitt, L. R. and Silver, D. R.. Stallings twists and the Jones polynomial. Preprint (1988).Google Scholar
[2]Jones, V. F. R.. Hecke algebra representations of braid groups and link polynomials. Ann. of Math. (2) 126 (1987), 335–388.CrossRefGoogle Scholar
[3]Kauffman, L. H.. State models and the Jones polynomial. Topology 26 (1987), 395–407.CrossRefGoogle Scholar
[4]Kouno, M., Motegi, K. and Shibuya, T.. Twisting and knot types. Preprint.Google Scholar
[5]Kouno, M., Motegi, K. and Shibuya, T.. Twisting of knots. Preprint.Google Scholar
[6]Morton, H. R.. Fibred knots with a given Alexander polynomial. Enseign. Math. 31 (1983), 206–222.Google Scholar
[7]Morton, H. R. and Strickland, P. M.. Jones polynomial invariants for knots and satellites. Math. Proc. Cambridge Philos. Soc. 109 (1991), 83–103.CrossRefGoogle Scholar
[8]Morton, H. R. and Traczyk, P.. Knots and algebras. Contribuciones Matematicas (1990).Google Scholar
[9]Murakami, J.. The Kauffman polynomial of links and representation theory. Osaka J. Math. 24 (1987), 745–758.Google Scholar
[10]Murakami, J.. The parallel version of polynomial invariants of links. Osaka J. Math. 26 (1989), 1–55.Google Scholar
[11]Whitehead, J. H. C.. On doubled knots. J. London Math. Soc. 12 (1937), 63–71.CrossRefGoogle Scholar