Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-16T13:08:35.679Z Has data issue: false hasContentIssue false
  • English
  • Français

Random symmetric matrices: rank distribution and irreducibility of the characteristic polynomial

Part of: Zeta and $L$-functions: analytic theory Special matrices

Published online by Cambridge University Press:  12 May 2022

ASAF FERBER ,
VISHESH JAIN ,
ASHWIN SAH  and
MEHTAAB SAWHNEY
ASAF FERBER
Affiliation:
340 Rowland Hall (Building 400), University of California, Irvine, Irvine CA 92697, U.S.A. e-mail: asaff@uci.edu
VISHESH JAIN
Affiliation:
390 Jane Stanford Way, Stanford, CA 94305, U.S.A. e-mail: visheshj@stanford.edu
ASHWIN SAH
Affiliation:
Simons Building (Building 2), 77 Massachusetts Avenue, Cambridge MA 02139, U.S.A. e-mails: asah@mit.edu, msawhney@mit.edu
MEHTAAB SAWHNEY
Affiliation:
Simons Building (Building 2), 77 Massachusetts Avenue, Cambridge MA 02139, U.S.A. e-mails: asah@mit.edu, msawhney@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

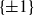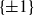Conditional on the extended Riemann hypothesis, we show that with high probability, the characteristic polynomial of a random symmetric $\{\pm 1\}$ -matrix is irreducible. This addresses a question raised by Eberhard in recent work. The main innovation in our work is establishing sharp estimates regarding the rank distribution of symmetric random $\{\pm 1\}$ -matrices over 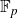$\mathbb{F}_p$ for primes $2 < p \leq \exp(O(n^{1/4}))$ . Previously, such estimates were available only for $p = o(n^{1/8})$ . 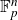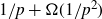At the heart of our proof is a way to combine multiple inverse Littlewood–Offord-type results to control the contribution to singularity-type events of vectors in $\mathbb{F}_p^{n}$ with anticoncentration at least $1/p + \Omega(1/p^2)$ . Previously, inverse Littlewood–Offord-type results only allowed control over vectors with anticoncentration at least 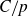$C/p$ for some large constant 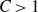$C > 1$ .

MSC classification

Primary: 15B52: Random matrices
Secondary: 11M50: Relations with random matrices
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 2 , March 2023 , pp. 233 - 246
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported in part by NSF grants DMS-1954395 and DMS-1953799.

‡

Sah and Sawhney were supported by NSF Graduate Research Fellowship Program DGE-1745302.

References

REFERENCES

Bary–Soroker, L., Koukoulopoulos, D. and Kozma, G.. Irreducibility of random polynomials: general measures, arXiv:2007.14567.Google Scholar
Bary–Soroker, L. and Kozma, G.. Irreducible polynomials of bounded height. Duke Math. J. 169 (2020), 579–598.Google Scholar
Breuillard, E. and Varjú, P. P.. Irreducibility of random polynomials of large degree. Acta Math. 223 (2019), 195–249.CrossRefGoogle Scholar
Campos, M., Jenssen, M., Michelen, M. and Sahasrabudhe, J.. Singularity of random symmetric matrices revisited. arXiv:2011.03013.Google Scholar
Campos, M., Jenssen, M., Michelen, M. and Sahasrabudhe, J.. The singularity probability of a random symmetric matrix is exponentially small. arXiv:2105.11384.Google Scholar
Campos, M., Mattos, L., Morris, R. and Morrison, N.. On the singularity of random symmetric matrices. Duke Math J. (2020), to appear.CrossRefGoogle Scholar
Costello, K. P., Tao, T. and Vu, V.. Random symmetric matrices are almost surely nonsingular. Duke Math. J. 135 (2006), 395–413.CrossRefGoogle Scholar
Eberhard, S.. The characteristic polynomial of a random matrix. arXiv:2008.01223.Google Scholar
Ferber, A.. Singularity of random symmetric matrices–simple proof. arXiv:2006.07439.Google Scholar
Ferber, A. and Jain, V.. Singularity of random symmetric matrices—a combinatorial approach to improved bounds. Forum of Mathematics, Sigma, vol. 7 (Cambridge University Press, 2019).CrossRefGoogle Scholar
Ferber, A., Jain, V., Luh, K. and Samotij, W.. On the counting problem in inverse Littlewood–Offord theory. arXiv:1904.10425.Google Scholar
Fulman, J. and Goldstein, L.. Stein’s method and the rank distribution of random matrices over finite fields. Ann. Probab. 43 (2015), 1274–1314.Google Scholar
Jain, V.. Approximate Spielman–Teng theorems for the least singular value of random combinatorial matrices. arXiv:1904.10592.Google Scholar
Jain, V., Sah, A. and Sawhney, M.. On the smallest singular value of symmetric random matrices. arXiv:2011.02344.Google Scholar
Koenig, J. and Nguyen, H.. Rank of near uniform matrices. arXiv:2101.00107.Google Scholar
Luh, K., Meehan, S. and Nguyen, H.. Random matrices over finite fields: methods and results. arXiv:1907.02575.Google Scholar
Maples, K.. Singularity of random matrices over finite fields. arXiv:1012.2372.Google Scholar
Maples, K.. Symmetric random matrices over finite fields, announcement. http://user.math.uzh.ch/maples/maples.symma.pdf.Google Scholar
Nguyen, H., Tao, T. and Vu, V.. Random matrices: tail bounds for gaps between eigenvalues. Probab. Theory Related Fields 167 (2017), 777–816.CrossRefGoogle Scholar
Nguyen, H. H. and Vu, V. H.. Optimal inverse Littlewood–Offord theorems. Advances in Mathematics 226 (2011), 5298–5319.CrossRefGoogle Scholar
Odlyzko, A. M. and Poonen, B.. Zeros of polynomials with 0,1 coefficients. Enseign. Math. (2) 39 (1993), 317–348.Google Scholar
Rudelson, M. and Vershynin, R.. The Littlewood–Offord problem and invertibility of random matrices. Adv. Math. 218 (2008), 600–633.Google Scholar
Tao, T. and Vu, V. H.. Inverse Littlewood-Offord theorems and the condition number of random discrete matrices. Ann. of Math. (2009), 595–632.CrossRefGoogle Scholar
Vershynin, R.. Invertibility of symmetric random matrices. Random Structures Algorithms 44 (2014), 135–182.CrossRefGoogle Scholar
Vu, V. H.. Recent progress in combinatorial random matrix theory. Probability Surveys 18 (2021), 179–200.CrossRefGoogle Scholar