Article contents
Proof of the Brown–Erdős–Sós conjecture in groups
Published online by Cambridge University Press: 04 July 2019
Abstract
The conjecture of Brown, Erdős and Sós from 1973 states that, for any k ≥ 3, if a 3-uniform hypergraph H with n vertices does not contain a set of k +3 vertices spanning at least k edges then it has o(n2) edges. The case k = 3 of this conjecture is the celebrated (6, 3)-theorem of Ruzsa and Szemerédi which implies Roth’s theorem on 3-term arithmetic progressions in dense sets of integers. Solymosi observed that, in order to prove the conjecture, one can assume that H consists of triples (a, b, ab) of some finite quasigroup Γ. Since this problem remains open for all k ≥ 4, he further proposed to study triple systems coming from finite groups. In this case he proved that the conjecture holds also for k = 4. Here we completely resolve the Brown–Erdős–Sós conjecture for all finite groups and values of k. Moreover, we prove that the hypergraphs coming from groups contain sets of size 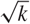 $\Theta (\sqrt k )$ which span k edges. This is best possible and goes far beyond the conjecture.
$\Theta (\sqrt k )$ which span k edges. This is best possible and goes far beyond the conjecture.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 169 , Issue 2 , September 2020 , pp. 323 - 333
- Copyright
- © Cambridge Philosophical Society 2019
Footnotes
The first and the second author were supported in part by SNSF grant 200021-175573.
Supported in part by ERC Starting Grant 633509 and ERC Starting Grant 676632.
References
REFERENCES
- 5
- Cited by


