Hostname: page-component-77c89778f8-7drxs Total loading time: 0 Render date: 2024-07-17T08:47:23.042Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomial expansions of positive harmonic functions in the unit ball

Published online by Cambridge University Press:  24 October 2008

D. H. Armitage
D. H. Armitage
Affiliation:
Department of Pure Mathematics, The Queen's University of Belfast
Get access Rights & Permissions [Opens in a new window]

Extract

It is well known that if h is harmonic in the open unit ball B of the Euclidean space 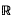N (where N ≥ 2), then there exist homogeneous harmonic polynomials Hn of degree n in 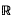N such that 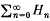converges absolutely and locally uniformly to h in B (see e.g. Brelot[2], appendice). Further, it is easy to show that this series is unique and that each polynomial Hn is the sum of all the monomial terms of degree n in the multiple Taylor series of h about the origin 0. We call 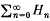the polynomial expansion of h. Our aim is to obtain sharp upper and lower bounds for the individual terms Hn and for the partial sums of this expansion in the case where h > 0 in B.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 110 , Issue 3 , November 1991 , pp. 533 - 544
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Armitage, D. H.. Spherical extrema of harmonic polynomials. J. London Math. Soc. (2) 19 (1979), 451–456.CrossRefGoogle Scholar
[2]Brelot, M.. Élements de la Théorie Classique du Potentiel (Centre de documentation universitaire, Paris, 1969).Google Scholar
[3]Beelot, M. and Choquet, G.. Polynômes Harmoniques et Polyharmoniques (Seconde colloque sur les équations aux dérivées partielles, Bruxelles, 1954).Google Scholar
[4]Carathéodory, C.. Über den Variabilitätsbereich der Fourierschen Konstanten von positiven harmonischen Funktionen. Rend. Circ. Mat. Palermo 32 (1911), 193–217.CrossRefGoogle Scholar
[5]Cooper, R.. The extremal values of Legendre polynomials and of certain related functions. Proc. Cambridge Philos. Soc. 46 (1950), 549–554.CrossRefGoogle Scholar
[6]Doob, J. L.. Classical Potential Theory and its Probabilistic Counterpart (Springer-Verlag, 1983).Google Scholar
[7]Goldstein, M. and Kuran, Ü.. On Harnack-type inequalities and the extremality of the Poisson kernel. Complex Variables Theory Appl. 9 (1988), 327–342.Google Scholar
[8]Müller, C.. Spherical Harmonics. Lecture Notes in Math. vol. 17 (Springer-Verlag, 1966).CrossRefGoogle Scholar
[9]Schur, I.. Über die Koeffizientensummen einer Potenzreihe mit positivem reelem Teil. Arch. Math. Phys. 27 (1918), 126–135.Google Scholar
[10]Szegö, G.. Koeffizientenabschätzungen bei ebenen und räumlichen harmonischen Entwicklungen. Math. Ann. 96 (1927), 601–632.CrossRefGoogle Scholar
[11]Szegö, G.. Orthogonal Polynomials (American Mathematical Society, 1967).Google Scholar
[12]Watson, G. N.. A Treatise on the Theory of Bessel Functions (Cambridge University Press, 1922).Google Scholar