Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-17T21:30:11.054Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Sum of Differentiable Functions

Published online by Cambridge University Press:  24 October 2008

H. T. Croft
H. T. Croft
Affiliation:
Peterhouse, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Ryll-Nardzewski has proposed the following problem (New Scottish Book, no. 119). If fn(x) are continuous, differentiable* functions in a closed finite interval, do there always exist constants cn (no cn = 0) (depending on the 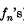), such that 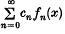converges and is also a continuous differentiable function?

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 2 , April 1962 , pp. 225 - 228
Copyright
Copyright © Cambridge Philosophical Society 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Throughout this article,‘differentiable’ means:‘with a finite (two-sided) derivative at every point’; this derivative may be unbounded. Thus is diffierentiable at x = 0; yẏ=⅓ is not.Google Scholar

† We shall assume this condition implicitly in all the work that follows.Google Scholar

‡ More generally, would also display all the relevant phenomena.Google Scholar

§ A's are absolute constants. O(1), o(l) refer to K →∞.Google Scholar