Article contents
On the set of zero coefficients of a function satisfying a linear differential equation
Published online by Cambridge University Press: 22 February 2012
Abstract
Let K be a field of characteristic zero and suppose that f: 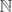 → K satisfies a recurrence of the form
→ K satisfies a recurrence of the form
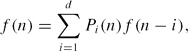 \[
f(n) = \sum_{i=1}^d P_i(n) f(n-i),
\]
\[
f(n) = \sum_{i=1}^d P_i(n) f(n-i),
\]
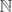 for which f(n) = 0 is a union of finitely many arithmetic progressions and a finite set. This generalizes the Skolem–Mahler–Lech theorem, which assumes that f(n) satisfies a linear recurrence. We discuss examples and connections to the set of zero coefficients of a power series satisfying a homogeneous linear differential equation with rational function coefficients.
for which f(n) = 0 is a union of finitely many arithmetic progressions and a finite set. This generalizes the Skolem–Mahler–Lech theorem, which assumes that f(n) satisfies a linear recurrence. We discuss examples and connections to the set of zero coefficients of a power series satisfying a homogeneous linear differential equation with rational function coefficients.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 153 , Issue 2 , September 2012 , pp. 235 - 247
- Copyright
- Copyright © Cambridge Philosophical Society 2012
References
REFERENCES
- 5
- Cited by


