In this paper, we shall prove a result which identifies the differentials in the Adams spectral sequence (see (1,2)) with certain cohomology operations of higher kinds, in the sense of (4). This theorem will be stated precisely at the end of section 2, after a summary of the necessary information about the Adams spectral sequence and higher-order cohomology operations; the proof will follow in section 3. Finally, in section 4, we shall consider, by way of example, the Adams spectral sequence for the stable homotopy groups of spheres: we show how our theorem gives a proof of Liulevicius's result that 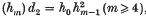, where the elements hn (n ≥ 0) are base elements of

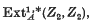
corresponding to the elements Sq2n in A, the mod 2 Steenrod algebra.