Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Orhan, C.
and
Yardimci, Ş.
2004.
Banach and Statistical Cores of Bounded Sequences.
Czechoslovak Mathematical Journal,
Vol. 54,
Issue. 1,
p.
65.
Mursaleen, M.
2011.
On A-invariant mean and A-almost convergence.
Analysis Mathematica,
Vol. 37,
Issue. 3,
p.
173.
Mursaleen, M.
and
Mohiuddine, S. A.
2014.
Convergence Methods for Double Sequences and Applications.
p.
1.
Cakalli, Huseyin
and
Taylan, Iffet
2018.
A variation on absolutely almost convergence.
Vol. 1978,
Issue. ,
p.
380005.


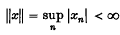 . A linear functional
. A linear functional 