Hostname: page-component-7479d7b7d-wxhwt Total loading time: 0 Render date: 2024-07-13T21:47:22.179Z Has data issue: false hasContentIssue false
  • English
  • Français

Lines, circles, focal and symmetry sets

Published online by Cambridge University Press:  24 October 2008

J. W. Bruce
J. W. Bruce
Affiliation:
Department of Pure Mathematics, University of Liverpool, P.O. Box 147, Liverpool, L69 3BX
Get access Rights & Permissions [Opens in a new window]

Extract

Let X be a surface in Euclidean 3-space, hereafter denoted by ℝ3. In the paper [13] Montaldi considered the contact of the surface X with circles, and obtained some very attractive results. In this piece of work we want to address some more detailed questions concerning such contact. In keeping with a general theme within singularity theory we shall bundle the circles up into fibres of certain maps and consider the restriction of these mappings to our surface X. In other words we shall be interested in the simultaneous contact of the surface X with special families of circles. The particular families we shall consider are parameterized by the set K of all lines in ℝ3; associated to such a line we have the family of all circles lying in planes orthogonal to the line, and centred on the line. The line will be referred to as the axis of the circle. Suppose, for example, the line in question is given by x1 = x2 = 0. We can consider the map ℝ3 → ℝ2 given by 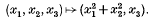. The fibres of this mapping are clearly the set of circles with the properties described above together, of course, with single points on the line itself. So the family of oriented lines parameterizes a family of mappings ℝ3 → ℝ2, and by restriction a family of mappings X → ℝ2. It is of interest to relate the singularities of this mapping to the differential geometry of X. The key geometric invariant of any smooth family is its bifurcation set, that is the set of parameter values for which the corresponding map fails to be stable. We shall see that for the family of circle maps the bifurcation set is of some interest.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 118 , Issue 3 , November 1995 , pp. 411 - 436
Copyright
Copyright © Cambridge Philosophical Society 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arnold, V. I., Gussein-Zade, S. M. and Varchenko, A. N.. Singularities of differentiable maps, Volume I (Birkhauser, 1986).Google Scholar
[2]Banchoff, T., Gaffney, T. J. and McCrory, C.. Cusps of Gauss mappings (Pitman, 1982).Google Scholar
[3]Bruce, J. W.. On contact of hypersurfaces. Bull. London Math. Soc. 13 (1981), 51–54.CrossRefGoogle Scholar
[4]Bruce, J. W.. Lines, surfaces and duality. Math. Proc. Camb. Phil. Soc. 112 (1992), 53–61.CrossRefGoogle Scholar
[5]Bruce, J. W.. Generic geometry, transversality and projections. J. London Math. Soc. (2) 49 (1994), 183–194.CrossRefGoogle Scholar
[6]Bruce, J. W. and Gaffney, T. J.. Simple singularities of mappings from ℂ to ℂ2. J. London Math. Soc. 26 (1982), 465–474.CrossRefGoogle Scholar
[7]Bruce, J. W. and Giblin, P. J.. Curves and singularities (Cambridge University Press, 1984).Google Scholar
[8]Bruce, J. W., Giblin, P. J. and Gibson, C. G.. Symmetry sets. Proc. Royal Soc. Edin. 104A (1986), 179–204.CrossRefGoogle Scholar
[9]Bruce, J. W. and Du Plessis, A. A.. Complete transversals, preprint, University of Liverpool, 1993.Google Scholar
[10]Bruce, J. W. and Romero-Fuster, M. C.. Duality and projections of curves and surfaces in 3-space. Quart. J. Math. Oxford 42 (1991), 433–441.CrossRefGoogle Scholar
[11]Bruce, J. W. and Wilkinson, T. C.. Folding maps and focal sets. Proceedings of Warwick Symposium on Singularities, Lecture Notes in Math. vol. 1462 (Springer-Verlag, 1991).Google Scholar
[12]Montaldi, J. A.. On generic composites of maps. Bull. Land. Math. Soc. 23 (1991), 81–85.CrossRefGoogle Scholar
[13]Montaldi, J. A.. Surfaces in 3-space and their contact with circles. J. Differential Geometry 23 (1986), 109–126.CrossRefGoogle Scholar
[14]Plessis, A. A. Du. On the determinacy of smooth map-germs. Invent. Math. 58 (1980), 107–160.CrossRefGoogle Scholar
[15]Porteous, I. R.. The normal singularities of surfaces in ℝ3. Proceedings of Symposia in Pure Mathematics, Volume 40, Part 2, 379–394 (American Mathematical Society, 1983).Google Scholar
[16]Rieger, J. H.. Families of maps from the plane to the plane. J. London Math. Soc. (2) 36 (1987), 351–369.CrossRefGoogle Scholar
[17]Rieger, J. H. and Ruas, M. A. S.. Classification of A-simple germs from kn to k2. Compositio Math. 79 (1991), 99–108.Google Scholar
[18]Shcherbak, O. P.. Projectively dual space curves and Legendre singularities. Trudy Tbiliss. Univ. 232–233 (1982), 280–336.Google Scholar
[19]Wall, C. T. C.. Finite determinacy of smooth map germs. Bull. Land. Math. Soc. 13 (1981), 481–539.CrossRefGoogle Scholar
[20]Wall, C. T. C.. Geometric properties of generic differentiable manifolds. Geometry and Topology, Rio de Janeiro 1976, Lecture Notes in Math. vol. 597 (Springer-Verlag, 1978), pp. 707–774.Google Scholar
[21]Whitney, H.. On singularities of mappings of Euclidean spaces I, Mappings from the plane to the plane. Ann. of Math. 62 (1955), 374–410.CrossRefGoogle Scholar