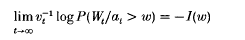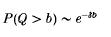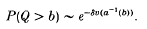Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Duffield, N.G.
Lewis, J.T.
O'Connell, N.
Russell, R.
and
Toomey, F.
1995.
Predicting quality of service for traffic with long-range fluctuations.
Vol. 1,
Issue. ,
p.
473.
Norros, I.
1995.
The management of large flows of connectionless traffic on the basis of self-similar modeling.
Vol. 1,
Issue. ,
p.
451.
Botvich, D. D.
and
Duffield, N. G.
1995.
Large deviations, the shape of the loss curve, and economies of scale in large multiplexers.
Queueing Systems,
Vol. 20,
Issue. 3-4,
p.
293.
Willinger, Walter
Taqqu, Murad S.
Sherman, Robert
and
Wilson, Daniel V.
1995.
Self-similarity through high-variability.
ACM SIGCOMM Computer Communication Review,
Vol. 25,
Issue. 4,
p.
100.
Beran, J.
Sherman, R.
Taqqu, M.S.
and
Willinger, W.
1995.
Long-range dependence in variable-bit-rate video traffic.
IEEE Transactions on Communications,
Vol. 43,
Issue. 2/3/4,
p.
1566.
Norros, I.
1995.
On the use of fractional Brownian motion in the theory of connectionless networks.
IEEE Journal on Selected Areas in Communications,
Vol. 13,
Issue. 6,
p.
953.
Duffield, N.G.
Lewis, J.T.
O'Connell, N.
Russell, R.
and
Toomey, F.
1995.
Entropy of ATM traffic streams: a tool for estimating QoS parameters.
IEEE Journal on Selected Areas in Communications,
Vol. 13,
Issue. 6,
p.
981.
Anantharam, V.
1995.
On the sojourn time of sessions at an ATM buffer with long-range dependent input traffic.
Vol. 1,
Issue. ,
p.
859.
Konstantopoulos, T.
and
Si-Jian Lin
1996.
High variability versus long-range dependence for network performance.
Vol. 2,
Issue. ,
p.
1354.
Duffield, N. G.
1996.
Economies of scale in queues with sources having power-law large deviation scalings.
Journal of Applied Probability,
Vol. 33,
Issue. 03,
p.
840.
Le-Sheng Chou
and
Cheng-Shang Chang
1996.
Experiments of the theory of effective bandwidth for Markov sources and video traces.
Vol. 2,
Issue. ,
p.
497.
Cheng-Shang Chang
Chi-Chao Chao
and
Thomas, J.A.
1996.
Fundamental limits of traffic regulation and their connections to source coding.
Vol. 1,
Issue. ,
p.
791.
Parulekar, M.
and
Makowski, A.M.
1996.
Tail probabilities for a multiplexer with self-similar traffic.
Vol. 3,
Issue. ,
p.
1452.
Duffield, N. G.
1996.
Economies of scale in queues with sources having power-law large deviation scalings.
Journal of Applied Probability,
Vol. 33,
Issue. 3,
p.
840.
Hongbo Zhu
and
Frost, V.S.
1996.
In-service monitoring for cell loss quality of service violations in ATM networks.
IEEE/ACM Transactions on Networking,
Vol. 4,
Issue. 2,
p.
240.
Liu, Zhen
Nain, Philippe
and
Towsley, Don
1997.
Exponential bounds with applications to call admission.
Journal of the ACM,
Vol. 44,
Issue. 3,
p.
366.
Knightly, Edward W.
1997.
Second moment resource allocation in multi-service networks.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 25,
Issue. 1,
p.
181.
Parulekar, M.
and
Makowski, A.M.
1997.
M|G|∞ input processes: a versatile class of models for network traffic.
Vol. 2,
Issue. ,
p.
419.
Willinger, W.
Taqqu, M.S.
Sherman, R.
and
Wilson, D.V.
1997.
Self-similarity through high-variability: statistical analysis of Ethernet LAN traffic at the source level.
IEEE/ACM Transactions on Networking,
Vol. 5,
Issue. 1,
p.
71.
Jelenkovic, P.R.
and
Lazar, A.A.
1997.
Multiplexing on-off sources with subexponential on periods.
Vol. 1,
Issue. ,
p.
187.