Complex bundles with two sections
Published online by Cambridge University Press: 24 October 2008
Extract
Atiyah(2) defined the geometrical dimension of an element 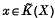 to be less than k + 1 (g dim (x) ≤ k) if there is a k-dimensional bundle over X whose stable equivalence class is x. If ξ is an n-plane complex bundle over X, we say that it has r sections if there is an (n − r)-plane bundle η such that ξ is isomorphic to η ⊕ εr where εr is the trivial r-plane bundle over X. If X has dimension 2n or less, then ξ has r sections if and only if g dim (ξ − n) ≤ n − r.
to be less than k + 1 (g dim (x) ≤ k) if there is a k-dimensional bundle over X whose stable equivalence class is x. If ξ is an n-plane complex bundle over X, we say that it has r sections if there is an (n − r)-plane bundle η such that ξ is isomorphic to η ⊕ εr where εr is the trivial r-plane bundle over X. If X has dimension 2n or less, then ξ has r sections if and only if g dim (ξ − n) ≤ n − r.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 71 , Issue 3 , May 1972 , pp. 457 - 462
- Copyright
- Copyright © Cambridge Philosophical Society 1972
References
REFERENCES
- 5
- Cited by


