Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-19T00:07:09.088Z Has data issue: false hasContentIssue false
  • English
  • Français

An extension of the method of steepest descents

Published online by Cambridge University Press:  24 October 2008

C. Chester ,
B. Friedman  and
F. Ursell
C. Chester
Affiliation:
Institute of Mathematical Sciences New York University
B. Friedman
Affiliation:
Institute of Mathematical Sciences New York University
F. Ursell
Affiliation:
King's CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Abstract

In the integral

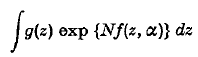
the functions g(z), f(z, α) are analytic functions of their arguments, and N is a large positive parameter. When N tends to ∞, asymptotic expansions can usually be found by the method of steepest descents, which shows that the principal contributions arise from the saddle points, i.e. the values of z at which ∂f/∂z = 0. The position of the saddle points varies with α, and if for some a (say α = 0) two saddle points coincide (say at z = 0) the ordinary method of steepest descents gives expansions which are not uniformly valid for small α. In the present paper we consider this case of two nearly coincident saddle points and construct uniform expansions as follows. A new complex variable u is introduced by the implicit relation

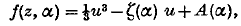
where the parameters ζ(α), A(α) are determined explicitly from the condition that the (u, z) transformation is uniformly regular near z = 0, α = 0 (see § 2 below). We show that with these values of the parameters there is one branch of the transformation which is uniformly regular. By taking u on this branch as a new variable of integration we obtain for the integral uniformly asymptotic expansions of the form

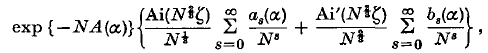
where Ai and Ai′ are the Airy function and its derivative respectively, and A(α), ζ(α) are the parameters in the transformation. The application to Bessel functions of large order is briefly described.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 53 , Issue 3 , July 1957 , pp. 599 - 611
Copyright
Copyright © Cambridge Philosophical Society 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Doetsch, G.Handbuch der Laplace-Transformation, vol. 2, ch. 3 (Basel, 1955).CrossRefGoogle Scholar
(2)Jeffreys, H. and Jeffreys, B. S.Methods of mathematical physics, 2nd ed. (Cambridge, 1950).Google Scholar
(3)Littlewood, J. E.Theory of functions (Oxford, 1944).Google Scholar
(4)Miller, J. C. P.The Airy integral. Brit. Assocn. Math. Tables Part-vol. B (Cambridge, 1946).Google Scholar
(5)Olver, F. W. J.Phil. Trans. A, 247 (1954), 307–27.Google Scholar
(6)Olver, F. W. J.Phil. Trans. A, 247 (1954), 328–68.Google Scholar
(7)Watson, G. N.Theory of Bessel functions, 2nd ed. (Cambridge, 1944).Google Scholar