Article contents
Semi-classical bound states of Schrödinger equations
Published online by Cambridge University Press: 21 October 2013
Abstract
We study the existence of semi-classical bound states of the nonlinear Schrödinger equation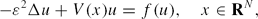 \begin{linenomath}$$ -\varepsilon^2\Delta u+V(x)u=f(u),\quad x\in {\bf R}^N,$$\end{linenomath}
\begin{linenomath}$$ -\varepsilon^2\Delta u+V(x)u=f(u),\quad x\in {\bf R}^N,$$\end{linenomath}
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 156 , Issue 1 , January 2014 , pp. 167 - 181
- Copyright
- Copyright © Cambridge Philosophical Society 2013
References
REFERENCES
- 1
- Cited by


