Article contents
Projective actions, invariant sigma-curves and quadratic functional equations
Published online by Cambridge University Press: 24 October 2008
Abstract
The quadratic functional equation f(f(x)) *–Tf(x) + Dx = 0 is equivalent to the requirement that the graph 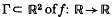 be invariant under a certain linear map
be invariant under a certain linear map 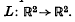 The induced projective map
The induced projective map  is used to show that the equation admits a rich supply of continuous solutions only when L is hyperbolic (T2 > 4D), and then only when T and D satisfy certain further conditions. The general continuous solution of the equation is given explicitly in terms of either (a) an expression involving an arbitrary periodic function, function additions, inverses and composites, or(b) suitable limits of such solutions.
is used to show that the equation admits a rich supply of continuous solutions only when L is hyperbolic (T2 > 4D), and then only when T and D satisfy certain further conditions. The general continuous solution of the equation is given explicitly in terms of either (a) an expression involving an arbitrary periodic function, function additions, inverses and composites, or(b) suitable limits of such solutions.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 98 , Issue 2 , September 1985 , pp. 195 - 212
- Copyright
- Copyright © Cambridge Philosophical Society 1985
References
REFERENCES
- 1
- Cited by


